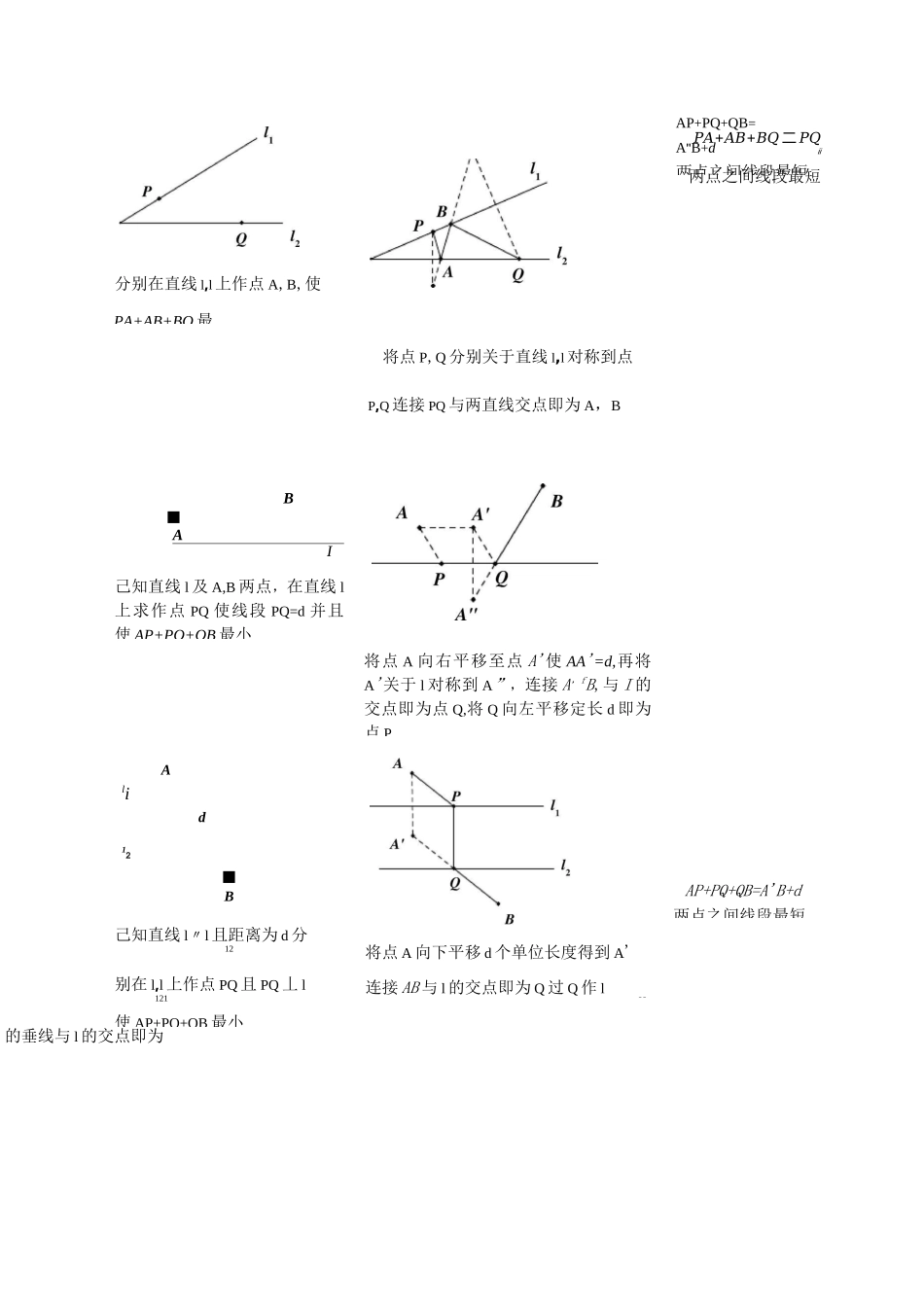
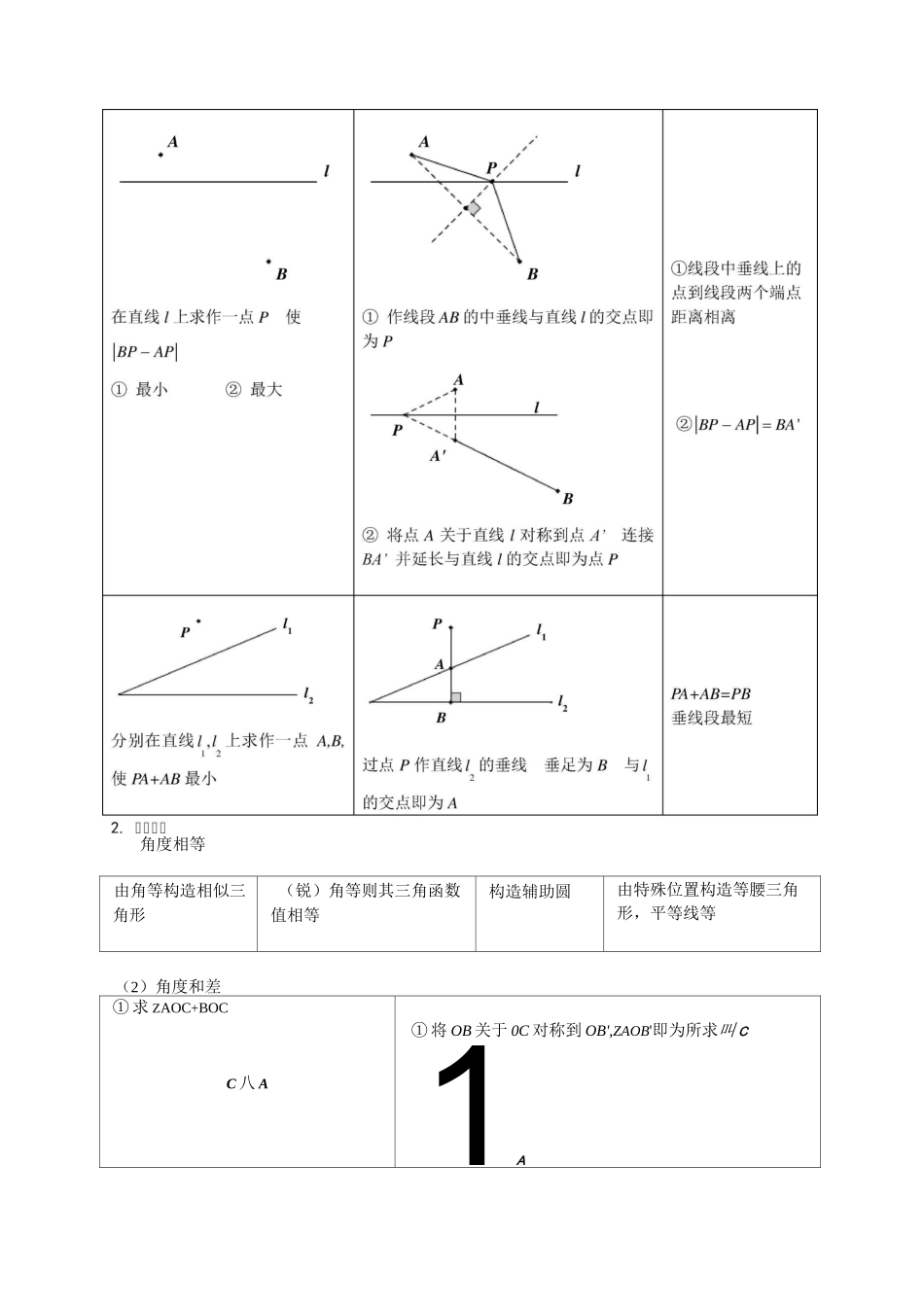
DDDDDDDDDDDDDD,DDDDD□.□□□□1.DDDDDD问题作法原理*BA*lAP+BP=A'B两点之间线段最短己知直线l及点A,B,在直线l上-/P■z作点P使AP+BP最小•A'将点对称到点A',连接A'B,与l的交点即为点P/p”VpZ.v_il2叫l2PA+AB+BP二PP12分别在直线l,l上作点A,B,12使iP2两点之间线段最短PA+AB+BP最小将点P分别关于直线l,l对称到点P,P1212连接P,P与两直线交点即为A,B12V11p1B;;1PA+AB+BQ二PQ11分别在直线l,l上作点A,B,12使V4Qi两点之间线段最短PA+AB+BQ最小将点P,Q分别关于直线l,l对称到点12P,Q连接PQ与两直线交点即为A,B1111分别在直线l,l上作点A,B,使12PA+AB+BQ最将点P,Q分别关于直线l,l对称到点21P,Q连接PQ与两直线交点即为A,B1111B■AI己知直线l及A,B两点,在直线l上求作点PQ使线段PQ=d并且使AP+PQ+QB最小AP+PQ+QB=A''B+d两点之间线段最短将点A向右平移至点A'使AA'=d,再将A'关于l对称到A”,连接A,fB,与I的交点即为点Q,将Q向左平移定长d即为点PAlid12■B己知直线l〃l且距离为d分12别在l,l上作点PQ且PQ丄l121使AP+PQ+QB最小AP+PQ+QB=A'B+d两点之间线段最短将点A向下平移d个单位长度得到A'连接AB与l的交点即为Q过Q作l22的垂线与l的交点即为PPA+AB+BQ二PQii两点之间线段最短角度相等由角等构造相似三角形(锐)角等则其三角函数值相等构造辅助圆由特殊位置构造等腰三角形,平等线等(2)角度和差①求ZAOC+BOCC八A①将OB关于0C对称到OB',ZAOB'即为所求叫C1A(3)特殊角BE4AFFBEA—EBCFAD构造等腰二角形ABC,可得gACF笥CBE构造正方形中的半角模型,利用旋转及其结论BC=BF+CD解决问题构造等腰直角二角形AEF中的半角模型,利用旋转及其结论BC2二BE2+CF2解决问题注:以上模型及结论均需构造并证明□□□□□□□□□□□□□□□□□□□□a1.在平面直角坐标系xOy中,抛物线y=x2+bx+c经过A(2,0),B(4,0)两点,直线y=1-x+2交y轴于点C,且过点D(8,m).(1)求抛物线的解析式(2)在x轴上找一点P使CP+DP的值最小,求出点P的坐标.(3)将抛物线y=x2+bx+c左右平移,记平移后点A的对应点为A',点B的对应点为B',当四边形A'B'DC的周长最小时,求平移后抛物线的解析式及此时四边形A'B'DC周长的最小值.(4)抛物线的顶点为Q,过点C作x轴的平行线l,点M在直线l上,且MN丄x轴,垂足为N,若DM+MN+NQ最小,直接写出此时点M,N的坐标.2.如下图所示,在平面直角坐标系xOy中,二次函数y=x2+bx+c的图像与x轴交于2.如下图所示,在平面直角坐标系xOy中,二次函数y=x2+bx+c的图像与x轴交于备用3.如下图所示,已知抛物线y=ax2+bx+1经过点A(l,3)和点B(2,1).(1)求此抛物线解析式.(2)点C,D分别是x轴和y轴上的动点,求四边形ABCD周长的最小值.(3)过点B作x轴的垂直,垂足为E点,点P从抛物线的顶点出发,先沿抛物线的对称轴到达F点,再沿EF到达E点,若P点在对称轴上的运动速度是它在直线EF上运动速度的^2倍,试确定点F的位置,使得点P按照上述要求到达E点所用的时间最短(要求:简述确定F点位置的方法,但不要求证明).4.抛物线y=-x2+bx+c与x轴交于点A、B,与y轴交于点C,已知A(-1,0),C(0,3).(1)求抛物线解析式.(2)点P为线段BC上任意一点,过点P作x轴的垂直交抛物线于点D,求线段DP长度的最大值及此时点D的坐标.(3)点Q为抛物线上一动点,且点Q到直线BC的距离等于|v2,求点Q的坐标.□□□□□□□□□□□□□□a5.在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=kx沿x轴向上平移3个单位长度后恰好经过B,C两占八、、•(1)求直线BC及抛物线的解析式.(2)设抛物线的顶点为D,点P在抛物线上的对称轴上,若①ZAPD=ZACB,②ZAPB=ZACB,分别求点P的坐标.(3)连接CD,求ZOCA与ZOCD两角和的度数.(4)已知点M(-2,0),点K是y轴右侧的抛物线图像上的一个动点,请直接写出锐角ZKCO>ZMCO时,点K的横坐标x的取值范围.6.如下图所示,已知抛物线y=ax2+bx+c与x轴交于点A(-2,0)、B(8,0),与y轴交于点C(0,-4),6.如下图所示,已知抛物线y=ax2+bx+c与x轴交于点A(-2,0)、B(8,0),与y轴交于点C(0,-4),7.如下图所示,抛物线y=ax2+bx-4a经过A(-1,0),C(0,4)两点,与x轴交于另一点B(1)求抛物线的解析式(2)已知...