自动控制原理VIP免费

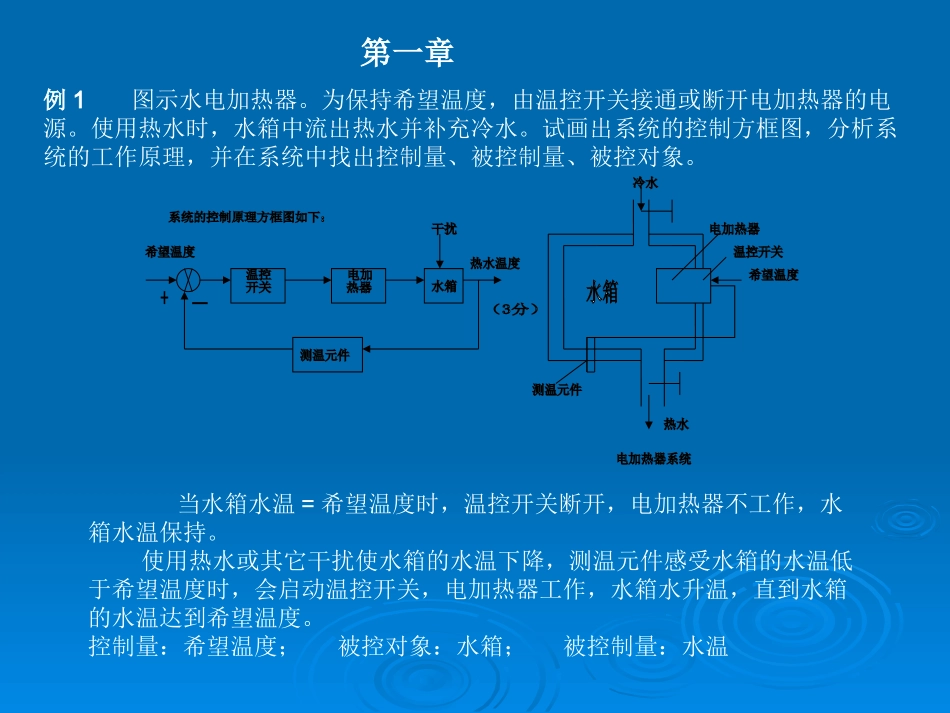
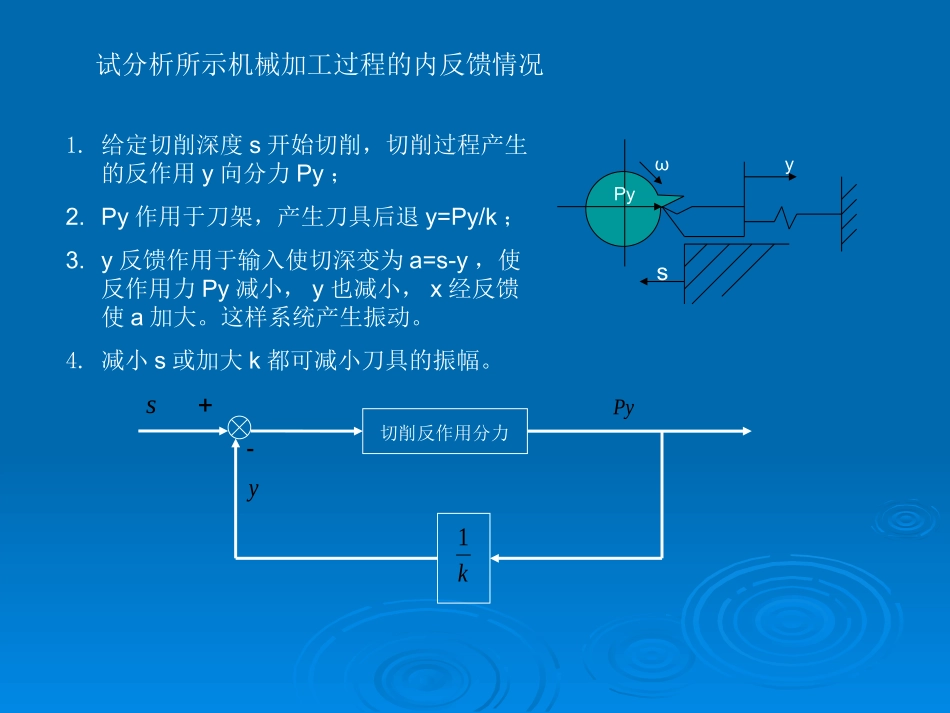
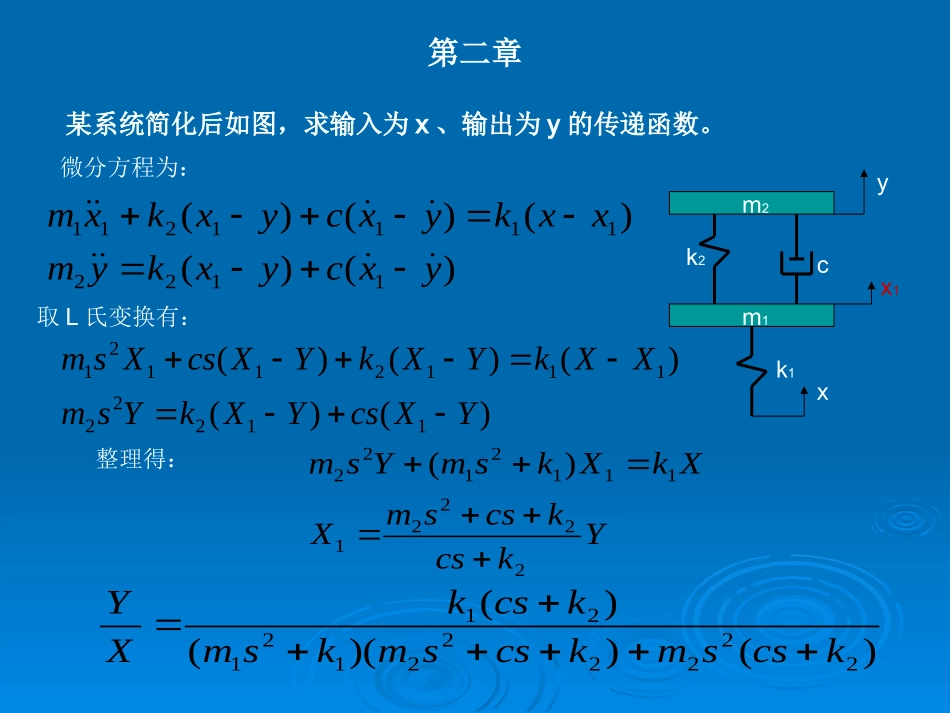
例1图示水电加热器。为保持希望温度，由温控开关接通或断开电加热器的电源。使用热水时，水箱中流出热水并补充冷水。试画出系统的控制方框图，分析系统的工作原理，并在系统中找出控制量、被控制量、被控对象。当水箱水温=希望温度时，温控开关断开，电加热器不工作，水箱水温保持。使用热水或其它干扰使水箱的水温下降，测温元件感受水箱的水温低于希望温度时，会启动温控开关，电加热器工作，水箱水升温，直到水箱的水温达到希望温度。控制量：希望温度；被控对象：水箱；被控制量：水温第一章试分析所示机械加工过程的内反馈情况yPysωsyPy切削反作用分力k11.给定切削深度s开始切削，切削过程产生的反作用y向分力Py；2.Py作用于刀架，产生刀具后退y=Py/k；3.y反馈作用于输入使切深变为a=s-y，使反作用力Py减小，y也减小，x经反馈使a加大。这样系统产生振动。4.减小s或加大k都可减小刀具的振幅。k1k2m1m2cyxx1)()()()()(11221111211yxcyxkymxxkyxcyxkxm)()()()()(1122211121121YXcsYXkYsmXXkYXkYXcsXsmYkcskcssmXXkXksmYsm222211112122)()())(()(22222212121kcssmkcssmksmkcskXY微分方程为：取L氏变换有：整理得：某系统简化后如图，求输入为x、输出为y的传递函数。第二章4.拉氏变换后即得传递函数)()()()(121srFssBsJssTrfBJT拉氏变换)()()()(22222sXkssXBsXmssFxkxBxmf拉氏变换sBJssrFsTs12)()()(sBJs121)(s)(sT)(sF)()()(222sXksBmssF)(sX)(sF222ksBms)()(srsXrx拉氏变换)(s)(sXr各环节的传递函数及方框图r系统方框图sBJs121)(sT)(sF)(sXr222ksBms)(s222212212222212)()()(1)(rksrBBsmrJrsBJsksBmsrsBJsrsGr系统传递函数(方框图化简)121111121111)(1)(1UIIsCIRudtiiCRi拉氏变换)(11)(1121122222112222IIsCIsCIRdtiiCdtiCRi拉氏变换22222211UIsCudtiC拉氏变换211111111IsCUIsCsCR1111sCRsC)(1sI)(1sU)(2sI11221212121IsCIsCCCCsCCR)(1sI)(2sI212122CCsCCRC)(2sI)(2sUsC21sC111111sCRsC)(1sI)(1sU)(2sI)(2sI212122CCsCCRC)(2sUsC21sC111)(1))(1()(22211122121221212111sCRCRCRsCCRRCCCsCCRsCRCsG按变量关系串连各环节传递函数方框图，得：化简方框图，得：已知某系统的传递函数方框如下图所示，其中，Xi(s)为输入，Xo(s)为输出，N(s)为干扰，试求：1.Xi(s)为输入，N(s)=0时，以Xo(s)为输出的传递函数；2．N(s)为输入，Xi(s)=0时，以Xo(s)为输出的传递函数；2121)1()(kkTsskksGx3．G(s)为何值时，系统可消除干扰的影响？G(s)12TsKsK1))1()()(()(21211kkTsskkkssGsGN。，kssG可消除干扰的影响时1)(解:1.2.3.U(s)+Y(s)s1)2(3ss-求如图系统的状态方程和输出方程。323)2(31)2(3)(232ssssssssG)(3)()32()()()(23ssUsYsssUsGsY即)(3)(3)(2)(tutytytyyxyxyx321uuuu2121321321300000203100010uuxxxxxx321)001()(xxxty系统的传递函数为：两边取L氏反变换有：令：系统的状态方程和输出方程为：第三章已知系统在非零初始条件下的单位阶跃响应为，若系统的传递函数的分子为常数，试求系统的传递函数。tteetx201)(由响应的形式可将系统的方程设为：（s=-1、s=-2为特征方程的根）232)(2sssG（A为待定常数）)121)0(1)0(('00xx)()(2)(3)(0'0"0tAxtxtxtxi故系统的方程为：由于为时的解，将它们代入方程有：tteetx201)(1)(txi2A)(2)(2)(3)(0'0"0txtxtxtxi故系统的传递函数为：已知系统微分方程为试用L氏变换的方法求初始条件为...