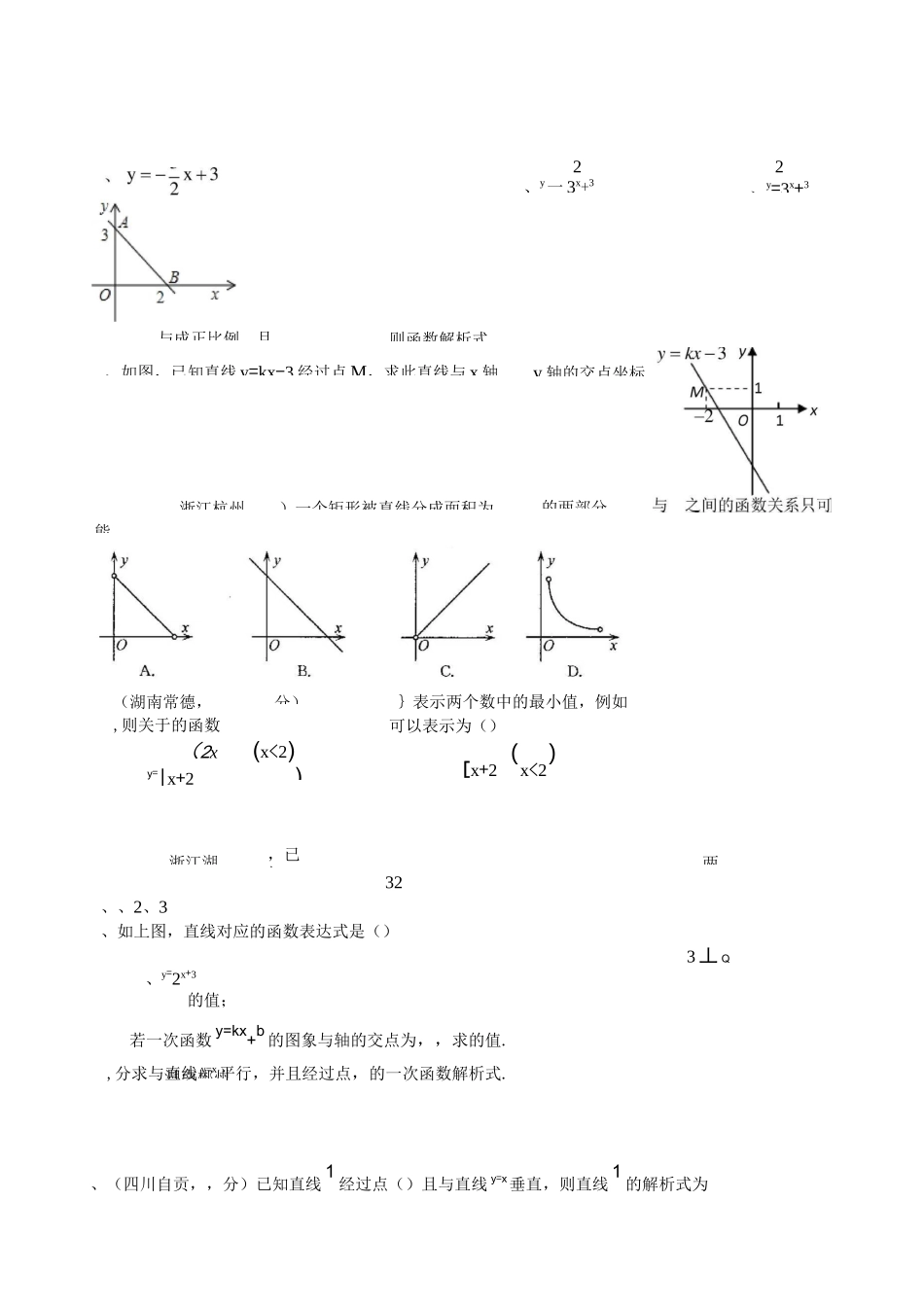
一次函数拔高讲义知识点、一次函数的意义习题练习、下列函数()n;次函数的有()1();()y=—;(x)y=—-8x;()y=5x2-4x+1中,2、个、个、个、个、当k时,y=(k~3)x2++2x-3是一次函数;、当时,y=(m-3)x2m+1+4x一5是-一次函数;、当时,y=(m-4)x2m+1+4x一5是-一次函数;知识点、求一次函数的解析式知识点:确定正比例函数y=kx的解析式:只须一个条件,求出待定系数k即可.确定一次函数y=kx+b的解析式:只须二个条件,求出待定系数k、b即可.、设——设出一次函数解析式,即y=kx+b;、代——把已知条件代入y=kx+b中,得到关于k、b的方程(组)、求一一解方程(组)求k、b;、写一一写出一次函数解析式.常见题型归类第一种情况:不已知函数类型(不可用待定系数法),通过寻找题目中隐含的自变量和函数变量之间的数量关系,建立函数解析式。(见前面函数解析式的确定)第二种情况:已知函数是一次函数(直接或间接),采用待定系数法。(已知是一次函数或已知解析式形式y=kx+b或已知函数图象是直线都是直接或间接已知了一次函数)一、定义型一次函数的定义:形如y=kx+b,k、为常数,且kMO。十住却卄心士小1y=kx+bly=kx+b、》k=kb丰b.l,,l小、丄、二平移型两条直线1:11;2:22。当12,12时,1〃2,解决问题时要抓住平行的直线k值相同这一特征。三两点型从几何的角度来看,“两点确定一条直线”,所以两个点的坐标确定直线的解析式;从代数的角度来说,一次函数的解析式y=kx+b中含两个待定系数k和,所以两个方程确定两个待定系数,因此想方设法找到两个点的坐标是解决问题的关键。解题策略:想方设法通过各种途径找到两个点的坐标,代入函数解析式中用待定系数法求出待定系数从而求出函数解析式。这类问题是见得最多的问题。四、探索型不直接已知函数类型,但可通过探索知其类型,再用待定系数法求解析式习题练习、已知(0,0),(,)两点,经过、两点的图象的解析式为()2、y一3x+32、y=3x+3与成正比例,且则函数解析式、如图,已知直线y=kx-3经过点M,求此直线与x轴,浙江杭州,,)一个矩形被直线分成面积为,(湖南常德,,则关于的函数(2xy=|x+2(x<2)(x>2)}表示两个数中的最小值,例如可以表示为()[x+2(x<2)y=|2x(x>2)浙江湖,已知:两湖南郴州32、、2、3、如上图,直线对应的函数表达式是()3丄Q、y=2x+3的值;若一次函数y=kx+b的图象与轴的交点为,,求的值.,分求与直线y=x平行,并且经过点,的一次函数解析式.、(四川自贡,,分)已知直线1经过点()且与直线y=x垂直,则直线1的解析式为y轴的交点坐标.的两部分,能,分)、(福建福州,()y二一x+1y=-x-1y-x+1y-x-1分)如图在平面直角坐标系中A、B均在边长为的正方形网格格点上、>-、V-、>、V、>、V、如图,、直求线段AB所在直线的函数解析式并写出当°'y'2时自变量x的取值范围;将线段AB绕点B逆时针旋转9°。得到线段BC请画出线段BC•若直线BC的函数解析式为y=kx+b则y随x的增大而填''增大”或''减小”).知识点、一次函数的图象b一次函数y=kx+b的图象是一条直线,与x轴的交点为(-,°),与y轴的交点为(°,b)k正比例函数y=kx的图象也是一条直线,它过点(°,°),(1,k)习题练习、一次函数的图象如图所示,当V时,的取值范围是()+与直线:=+在同一平面直角坐标系中的图象如图所示,则关于的不等+的解集为()式+V、(0山东枣庄,y—x0分)如图所示,函数yi14y—x+和233的图象相交于(一,),(,)两点.当yi>y2时,的取值范围是()A.V——VBV、(0贵州毕节,,分)已知一次函数y=kX+3的图象如图所示,则不等式kx+3<0的解集是、(0吉林长春,值范围是•9、(0青海西宁,+V—的解集为分)如图,一次函数y—k+b°<°)的图象经过点A.当y<3时,x的取和B0两点,则不等式0V0(0台湾台北,9)如图所示的坐标平面上,有一条通过点一一的直线。若四点一在上,则下列数值的判断,何者正确?°CV、(0内蒙古呼和浩特市,分)已知关于的一次函数y=mx+n的图象如图所示,则1n—m1—总可化简为、(0湖北鄂州,,分)如图,把RtAABC放在直角坐标系内,其中ZCAB=90°,BC=,点A、B的坐标分别为(,0)、(,0),将厶ABC沿轴向右平移,当点C落在直线=—...