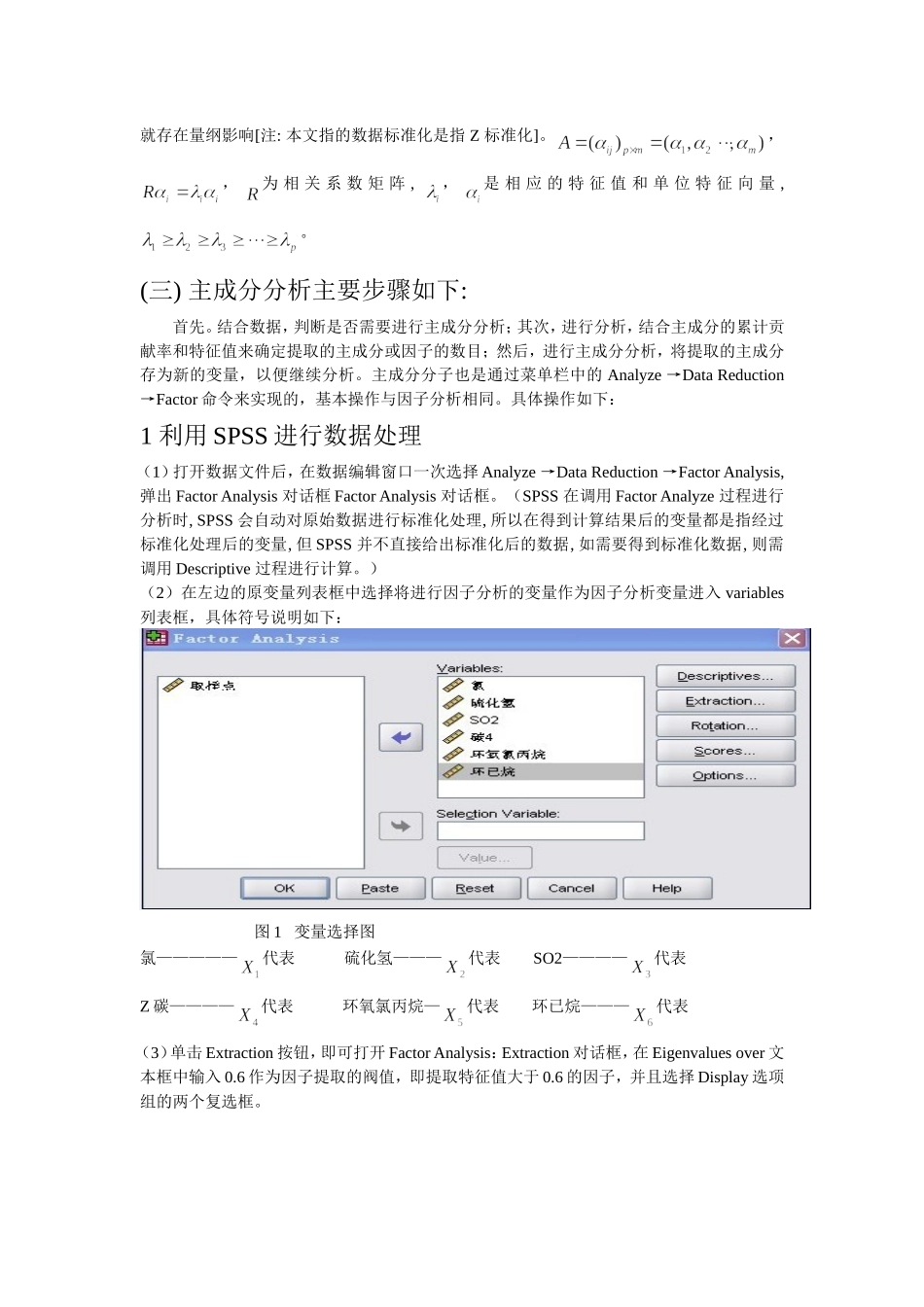
西南大学多元统计分析课程论文学院数学与统计学院年级专业2009级数学与应用数学论文写作唐维彬学号222009314012030资料收集李虹霖学号222009314012023软件操作刘鹏懿学号222009314012027数据分析冉俊峰学号222009314012029日期2012年10月30日基于主成分分析和因子分析评估大气污染摘要:近年来大气污染日趋严重,引起了人们的广泛关注。本文采用主成分分析法和因子分析法,为了评估某大型化工厂的污染情况,在厂区及邻近地区挑选有代表性的8个大气取样点,每日4次同时抽取大气样品,测定其中包含的6种气体的浓度,前后共4天,每个样品每种气体实测16次。最后通过数据的分析与整理,运用SPSS软件,进行主成分分析和因子分析,对该大型化工厂的污染情况做出评估,关键字:主成分分析因子分析SPSS17.0软件大气污染正文主成分分析法(一)主成分分析原理主成分分析是设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来代替原来的指标。通常数学上的处理就是将原来P个指标作线性组合,作为新的综合指标。最经典的做法就是用(选取的第一个线性组合,即第一个综合指标)的方差来表达,即Var()越大,表示包含的信息越多。因此。在所有的线性组合中选取的应该是方差最大的,故称为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考虑选取即选第二个线性组合,为了有效地反映原来信息,已有的信息就不需要再出现在中,用数学语言表达就是要求Cov(,)=0,则称为第二主成分,依此类推可以构造出第三、第四,,第P个主成分。(二)主成分分析数学模型其中,,,(i=1,,m)为X的协方差阵Σ的特征值多对应的特征向量,,,,是原始变量经过标准化处理的值,因为在实际应用中,往往存在指标的量纲不同,所以在计算之前须先消除量纲的影响,而将原始数据标准化,本文所采用的数据就存在量纲影响[注:本文指的数据标准化是指Z标准化]。,,为相关系数矩阵,,是相应的特征值和单位特征向量,。(三)主成分分析主要步骤如下:首先。结合数据,判断是否需要进行主成分分析;其次,进行分析,结合主成分的累计贡献率和特征值来确定提取的主成分或因子的数目;然后,进行主成分分析,将提取的主成分存为新的变量,以便继续分析。主成分分子也是通过菜单栏中的Analyze→DataReduction→Factor命令来实现的,基本操作与因子分析相同。具体操作如下:1利用SPSS进行数据处理(1)打开数据文件后,在数据编辑窗口一次选择Analyze→DataReduction→FactorAnalysis,弹出FactorAnalysis对话框FactorAnalysis对话框。(SPSS在调用FactorAnalyze过程进行分析时,SPSS会自动对原始数据进行标准化处理,所以在得到计算结果后的变量都是指经过标准化处理后的变量,但SPSS并不直接给出标准化后的数据,如需要得到标准化数据,则需调用Descriptive过程进行计算。)(2)在左边的原变量列表框中选择将进行因子分析的变量作为因子分析变量进入variables列表框,具体符号说明如下:图1变量选择图氯—————代表硫化氢———代表SO2————代表Z碳————代表环氧氯丙烷—代表环已烷———代表(3)单击Extraction按钮,即可打开FactorAnalysis:Extraction对话框,在Eigenvaluesover文本框中输入0.6作为因子提取的阀值,即提取特征值大于0.6的因子,并且选择Display选项组的两个复选框。图2因子提取(4)单击OK按钮,执行因子分析得到如下所示的特征值和方差贡献表以及因子负荷矩阵。下表为各因子对应的特征值,%ofVariance列为各因子的方差贡献率;Cumulative%列为累计方差贡献率。从表中可以看出,前4个变量已经可以解释89.264%的方差。表1特征值与方差贡献表下表为旋转前的因子负荷矩阵,与因子分析得到的结果是一致的。表2旋转前的因子负荷矩阵2利用因子分析的结果进行主成分分析(1)将旋转前的因子负荷矩阵中的数据输入到SPSS数据编辑窗口,将4个变量分别命名为A1A2A3和A4。图3新变量A1A2A3A4(2)然后,依次计算特征向量矩阵。在主菜单栏中选择Transform→ComputeVariable命令,打开如图所示的ComputeVariable对话框,“T1=A1/SQR(2.183)”,单击OK按钮,即可在数据编辑窗口中得到变量名为T1的第一特征变量。依次类...