中国石油大学工程流体力学例题等VIP免费

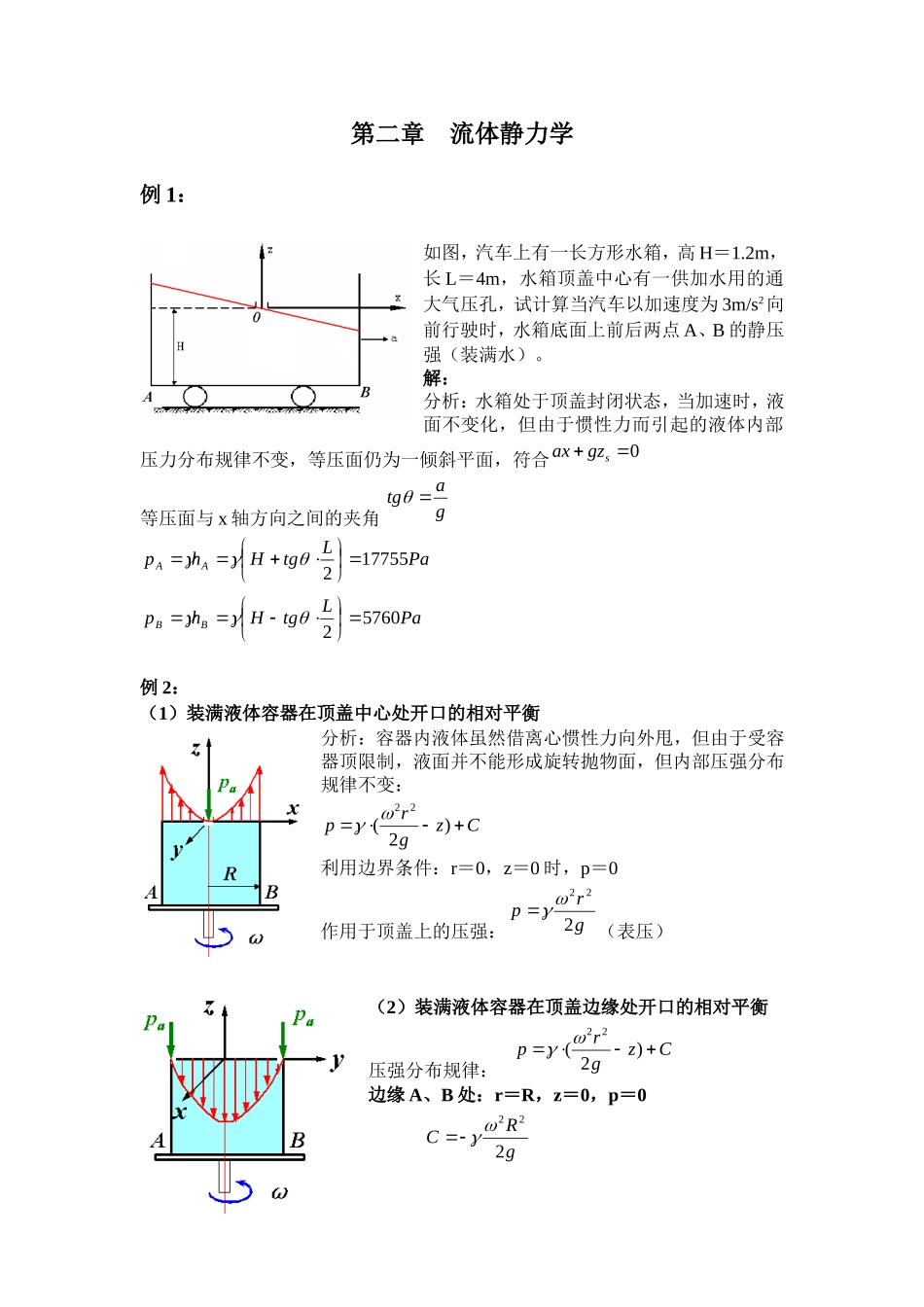
第一章流体及其主要物理性质例1：已知油品的相对密度为0.85，求其重度。解：3/980085.085.0mN例2：当压强增加5×104Pa时，某种液体的密度增长0.02%，求该液体的弹性系数。解：0dVVddMVMddVVPadpddpVdVEp84105.2105%02.01111例3：已知：A＝1200cm2，V＝0.5m/sμ1＝0.142Pa.s，h1＝1.0mmμ2＝0.235Pa.s，h2＝1.4mm求：平板上所受的内摩擦力F绘制：平板间流体的流速分布图及应力分布图解：（前提条件：牛顿流体、层流运动）dydu2221110huhuV因为τ1＝τ2所以smhhVhuhuhuV/23.02112212211NhuVAF6.411第二章流体静力学例1：如图，汽车上有一长方形水箱，高H＝1.2m，长L＝4m，水箱顶盖中心有一供加水用的通大气压孔，试计算当汽车以加速度为3m/s2向前行驶时，水箱底面上前后两点A、B的静压强（装满水）。解：分析：水箱处于顶盖封闭状态，当加速时，液面不变化，但由于惯性力而引起的液体内部压力分布规律不变，等压面仍为一倾斜平面，符合0sgzax等压面与x轴方向之间的夹角gatgPaLtgHhpAA177552PaLtgHhpBB57602例2：（1）装满液体容器在顶盖中心处开口的相对平衡分析：容器内液体虽然借离心惯性力向外甩，但由于受容器顶限制，液面并不能形成旋转抛物面，但内部压强分布规律不变：Czgrp)2(22利用边界条件：r＝0，z＝0时，p＝0作用于顶盖上的压强：grp222（表压）（2）装满液体容器在顶盖边缘处开口的相对平衡压强分布规律：Czgrp)2(22边缘A、B处：r＝R，z＝0，p＝0gRC222作用于顶盖上的压强：2222rRgp例3：已知：r1，r2，Δh求：ω0解：0212120szgr（1）0222220szgr（2）因为hzzss21所以212202rrhg例4已知：一圆柱形容器，直径D＝1.2m，完全充满水，顶盖上在r0＝0.43m处开一小孔，敞开测压管中的水位a＝0.5m，问此容器绕其立轴旋转的转速n多大时，顶盖所受的静水总压力为零？已知：D＝1.2m，r0＝0.43m，a＝0.5m求：n解：据公式)(ZdzYdyXdxdp坐标如图，则xX2，yY2，gZ代入上式积分：Czgrp)2(22（*）由题意条件，在A点处：r＝r0，z＝0，p＝γa则Cgra)02(202所以)2(202graC所以)2()2(20222grazgrp当z＝0时：)2(220222gragrp它是一旋转抛物方程：盖板上静压强沿径向按半径的二次方增长。而02)2(222022200rdrgragrrdrppdAPRRA所以0)2(2202320drrgragrR即02)2(420220242Rrgrarg则2202022224042RrgagarR所以22024212Rrgan代入数据得：n＝7.118转/秒例5：闸门宽1.2m，铰在A点，压力表G的读数为－14700Pa，在右侧箱中装有油，其重度γ0＝8.33KN/m3，问在B点加多大的水平力才能使闸门AB平衡？解：把p0折算成水柱高：mph5.19800147000相当于液面下移1.5m，如图示虚构液面则左侧：NAhPc7056022.11298001mAhJhhcccD11.311.0322.131222.11231压力中心距A点：3.11－2＝1.11m右侧：KNAhPco992.192.122233.82mAhJhhcccD33.122.111222.1132设在B点加水平力F使闸门AB平衡，对A点取矩∑MA＝0即ABFhPhPDD2211KNF87.25233.1992.1911.156.70例6：一示压水箱的横剖面如图所示，压力表的读数为0.14个大气压，圆柱体长L＝1.2m，半径R＝0.6m求：使圆柱体保持如图所示位置所需的各分力（圆柱体重量不计）。解：水平分力：→NAhPxcx2.119952.16.07.19800垂直分力：↑NVPz8.1320133912.0008.1980046.02.12.16.04.198002压第三章流体运动学与动力学基础例1：已知：0zyxutyutxu...