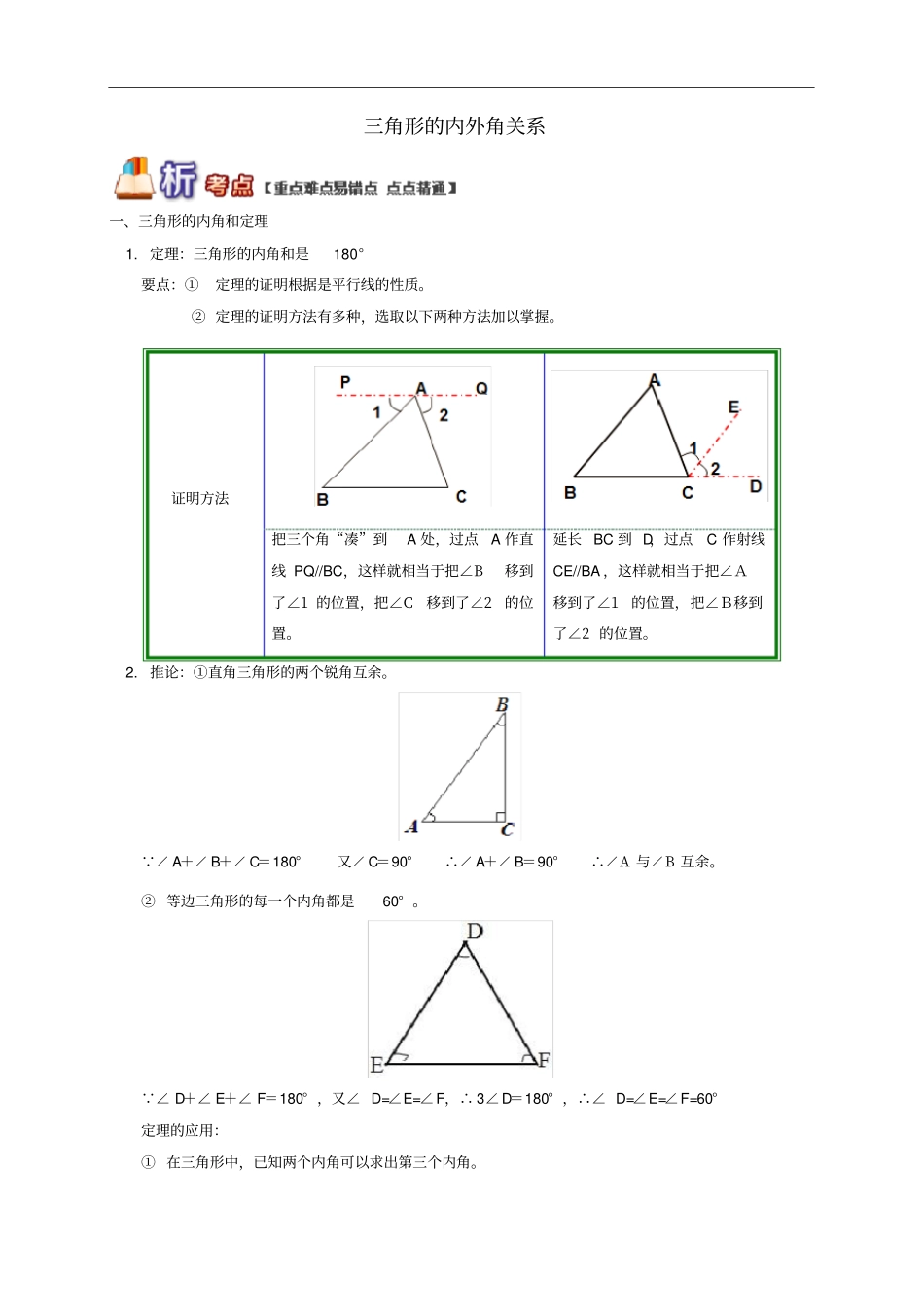
三角形的内外角关系一、三角形的内角和定理1.定理:三角形的内角和是180°要点:①定理的证明根据是平行线的性质。②定理的证明方法有多种,选取以下两种方法加以掌握。2.推论:①直角三角形的两个锐角互余。 ∠A+∠B+∠C=180°又∠C=90°∴∠A+∠B=90°∴∠A与∠B互余。②等边三角形的每一个内角都是60°。 ∠D+∠E+∠F=180°,又∠D=∠E=∠F,∴3∠D=180°,∴∠D=∠E=∠F=60°定理的应用:①在三角形中,已知两个内角可以求出第三个内角。证明方法把三个角“凑”到A处,过点A作直线PQ//BC,这样就相当于把∠B移到了∠1的位置,把∠C移到了∠2的位置。延长BC到D,过点C作射线CE//BA,这样就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置。如:在△ABC中,∠C=180°-(∠A+∠B)②在三角形中,已知三个内角和的比或它们之间的关系,求各内角。如:在△ABC中,已知∠A:∠B:∠C=2:3:4,则可设∠A、∠B、∠C为2x、3x、4x,利用方程求得度数。二、三角形的外角1.外角的定义:三角形一边与另一边的延长线组成的角,叫做三角形的外角。如∠ACD与∠BCE均为外角。2.三角形外角的性质(1)三角形的一个外角等于和它不相邻的两个内角之和。(2)三角形的一个外角大于任何一个与它不相邻的内角。提示:三角形每个顶点处有两个外角,它们是对顶角,所以三角形共有六个外角。通常每个顶点处取一个外角,因此,我们常说三角形有三个外角。因为三角形的每个外角与它相邻的内角是邻补角,由三角形的内角和是180°,可推出三角形的外角和是360°。三、三角形的外角与内角的关系1.三角形的一个外角与它相邻的内角互补,如图:∠1与∠4是邻补角,即∠1+∠4=180o;2.三角形的一个外角等于与它不相邻的两个内角的和,如图:∠1=∠2+∠3;3.三角形的一个外角大于与它不相邻的任何一个内角,如图:∠1>∠2,∠1>∠3。【拓展】方法归纳:三角形的内、外角关系的知识点应注意以下几点:(1)实际应用中,题目中往往把∠A+∠B+∠C=180°这个条件隐藏,要时时注意想到这个条件。(2)外角关系强调的是“不相邻”三个字,不要被题目偷换概念。(3)应用三角形的内、外角关系解题时,经常要使用到高、角平分线,注意二者定义中,高有垂直的结论,即有角是90°,角平分线的作用是将一个角平分成两个相等的角,有21角的数值存在。(4)三角形的内角和定理和三角形的外角的性质是求角度及与角有关的推理论证时常使用的理论依据,另外,在证明角的不等关系时也常想到外角的性质。技巧归纳:解决本部分习题时要注意几种数学思想的应用:两种图形的认识(1)对顶三角形:有一个角是对顶角的两个三角形。特点是:每个三角形中除对顶角外,另两个角的和与另一个三角形中其余两个角的和相等。如图:∠A+∠B=∠D+∠E(2)图形的折叠:将图形沿某条线折叠,使其一部分与图形中某部分重合,可以形成边、角等多个相等关系。如图:∠1=∠2=∠3方程的思想根据角与角之间的关系求角的度数时可列方程(或方程组)求解。如:∠A:∠B:∠C=1:2:3,求三角形的形状。整体运用的思想将待解决的问题看作一个整体,通过研究问题做整体处理后,达到解决问题的目的。如:∠A=40°,求∠3+∠4+∠B+∠C的度数。总结:1.学会综合运用内、外角关系解决图形的角度计算问题。2.将各种解题思想及方法掌握好,有利于今后几何的学习。例题1如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为()A.50°B.60°C.70°D.80°解析:先根据三角形的内角和定理求出∠4的度数,由对顶角的性质可得出∠5的度数,再由平行线的性质即可得出结论。答案: 在△BCD中,∠1=50°,∠2=60°,∴∠4=180°-∠1-∠2=180°-50°-60°=70°,∴∠5=∠4=70°, a∥b,∴∠3=∠5=70°。故选C。点拨:本题考查的是平行线的性质、三角形的内角和定理。解答此类题目时往往用到三角形的内角和是180°这一隐藏条件。例题2如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处。若∠A=22°,则∠BDC等于()转化的思想求较复杂的图形中多个角的度数和的问...