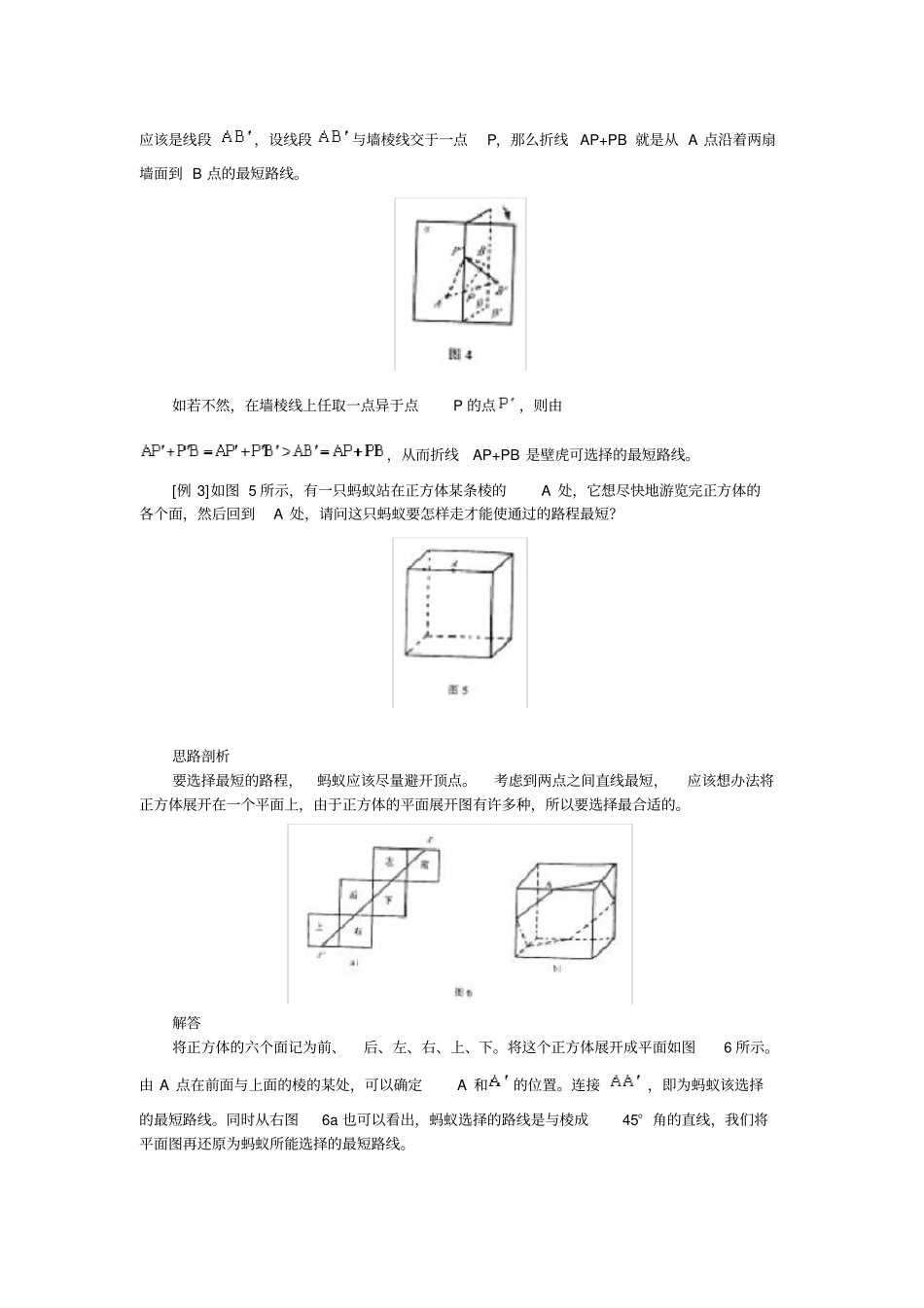
第17讲最短路线问题知识网络人们在日常生产、生活实践中,常常会遇到带有某种限制条件的最近路线即最短路线问题。通常最短路线问题是以“平面内连接两点的线中,直线段最短”为原则引申出来的。常见的最短路线问题,按研究问题的限制条件允许已知的两点所在面的不同,分成四类:(1)如果两点位于同一平面上,那么所求的最短路线是线段。(2)如果两点位于不同的不同的平面上,如凸多面体的表面,那么所求的最短路线是曲线。(3)如果两点位于可展开为平面的曲面上,如圆柱面、圆锥面,那么所求的最短路线是曲线。(4)如果两点位于不可展开为平面的曲面上,如球面,这时所求的最短路线是曲线。重点·难点最短路线问题的所有问题都是从一个基本定理引出来的:“两点之间,直线段最短。”如何将一些不能直接应用此定理的题型转化为可利用此定理的题型,是解决本讲问题的关键。这里常用“对称”的方法转化问题。学法指导对于平面上的最短路线问题,一般是尽量化简问题,使得能够应用基本定理。而凸多面体和可展开为平面的曲面的最短路线问题,是将它们展开为平面,将问题转化平面上的最短路线问题来解决。对不可展为平面的曲面,主要是球面,我们用以下面的这个具体例子来说明:设球面上有A、B两点,我们用过A点、B点及球心O的平面截球,在球的表面上留下的截痕为圆周(称大圆),在这个大圆周上A、B两点之间的不超过半个圆周的弧线就是所求的A、B两点间的最短路线。经典例题[例1]有一个牧马人带着马群从营房A点出发,到草地MN放牧。傍晚到营房B之前先带马群到小河PQ去给马饮水,如图1所示。想一想:牧人应该走哪一条路线,才能使整个放牧的路程(即从A→MN→PQ→B)最短?思路剖析考虑这个问题可先假设牧马人从A点先到达草地MN上的某点E,然后再从E到达小河岸PQ上的某点F,最后再从F点回到B点。依题意,本题是求A→E→F→B的这条路线最短。我们用对称法求解。解答如图2所求,首先,我们作A点关于草地MN的对称点,作B点关于小河PQ的对称点连接,交直线MN于点E,交直线PQ于点F,连接AE、BF,则折线段AE+EF+FB就是所求的最短路线。这是因为是A关于直线MN的对称点,所以;是B关于直线PQ的对称点,所以;因此。若在MN上有异于点E的点,PQ上有异于点F的点,显然有(因为、两点之间,直线段最短),从而,即A→E→F→B是符合题意的最短路线。[例2]如图3所示,一只壁虎要从一面墙壁α上A点,爬到邻近的另一面墙壁β上的B点捕飞蛾,它可以沿许多路径到达,请你为它选择一条最近的路线。思路剖析由于A、B两点位于不同的平面上,因此基本思想是将这两上平面通过翻转,使A、B两点能够位于同一平面上,而我们可通过沿顺时针方向将β面旋转90°来达到目的。解答我们假想把含B点所在的墙β顺时针旋转90度(如图4所示),这样这两面墙就处在同一个平面上,记此时β转过来的位置为,B点的位置为。则A、之间的最短路线应该是线段,设线段与墙棱线交于一点P,那么折线AP+PB就是从A点沿着两扇墙面到B点的最短路线。如若不然,在墙棱线上任取一点异于点P的点,则由,从而折线AP+PB是壁虎可选择的最短路线。[例3]如图5所示,有一只蚂蚁站在正方体某条棱的A处,它想尽快地游览完正方体的各个面,然后回到A处,请问这只蚂蚁要怎样走才能使通过的路程最短?思路剖析要选择最短的路程,蚂蚁应该尽量避开顶点。考虑到两点之间直线最短,应该想办法将正方体展开在一个平面上,由于正方体的平面展开图有许多种,所以要选择最合适的。解答将正方体的六个面记为前、后、左、右、上、下。将这个正方体展开成平面如图6所示。由A点在前面与上面的棱的某处,可以确定A和的位置。连接,即为蚂蚁该选择的最短路线。同时从右图6a也可以看出,蚂蚁选择的路线是与棱成45°角的直线,我们将平面图再还原为蚂蚁所能选择的最短路线。[例4]有一个圆锥如图7a所示A、B在同一条母线上,B为AO的中点,试求以A为起点,以B为终点且绕圆锥侧面一周的最短路线。思路剖析圆锥的侧面可展为一个平面图形(如图7b所示),其中若将OA、粘合起来,恰为图7a中的圆锥,并且B与重合。从而在扇形中是A点与点的最短路程。解答将圆锥面沿母线AO剪开,...