余弦函数的图象与性质VIP免费

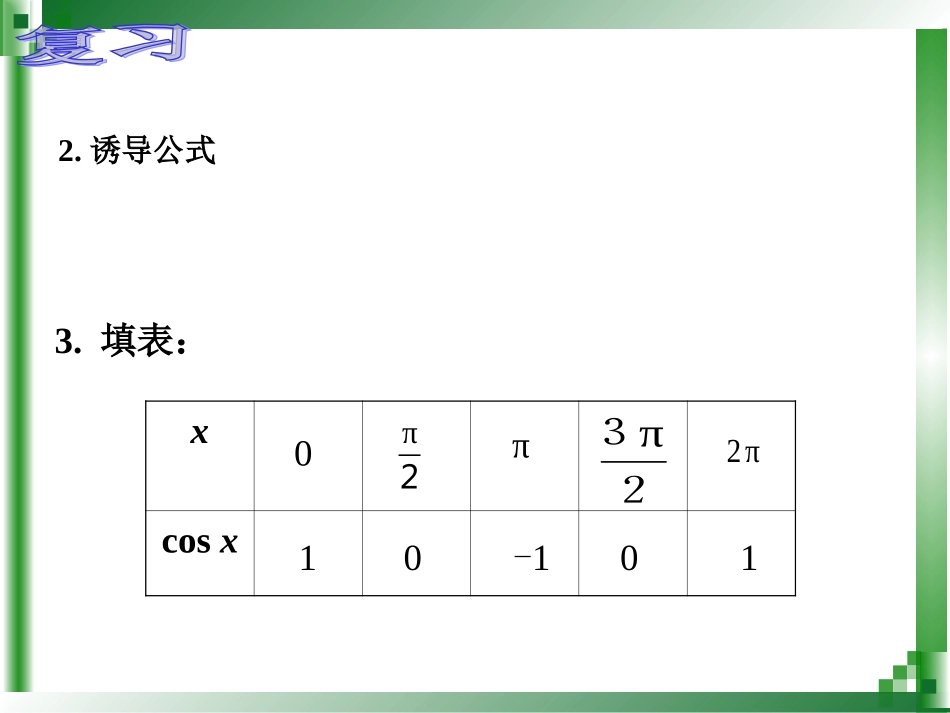
6.3.3余弦函数图象与性质2015.4.22yxo1-1223221、正弦函数的五点法作图(0,0)(,1)2(,0)(,-1)23(2,0)五点画图法五点法——(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)2.诱导公式xcosx２π２３ππ2π10-10103.填表：一、余弦函数的图象余弦函数图象的五个关键点：与x轴的交点，，２)0π()0π(，２３图象的最高点，，)10()1π2(，图象的最低点)1π(，oxy---11--13π2π3π26π5π6π73π42π33π56π11π26π五点作图法由诱导公式cos(x+2k)＝cosx，将y＝cosx，x[0，2]的图象沿x轴向左、右平移2，4，…，就可得到y＝cosx的图象.π2oπ4π62π4π6xy---------1-1余弦曲线二、余弦函数的性质定义域xR，值域y[-1，1].当x＝2k，kZ时，y＝cosx取得最大值1，即ymax＝1；当x＝(2k+1)，kZ时，y＝cosx取得最小值-1，即ymin＝-1．观察余弦曲线(1)余弦函数的值域由公式cos(x＋k·2)＝cosx(kZ)可知：余弦函数是一个周期函数，2，4，…，－2，－4，…，2k(kZ且k≠0)都是余弦函数的周期；2是其最小正周期．(2)余弦函数的周期余弦函数的图象每隔2重复出现．(3)余弦函数的奇偶性由公式cos(－x)＝cosx余弦函数是偶函数．图象关于y轴成轴对称．xo--1234-2-3-41y(4)余弦函数的单调性观察余弦曲线xcosx－1010－1在[(2k－1),2k](kZ)上，是增函数；在[2k，(2k＋1)](kZ)上，是减函数．yxo--12-2-312π2π32π52π2π32π5－……0……2π2π例1利用“五点法”作下列函数在上的简图（1）y＝1+cosx；(2)y＝2cosx2,0例1利用“五点法”作下列函数在上的简图（1）y＝1+cosx；(2)y＝2cosx2,0例2求下列函数的最大值，最小值和周期T：（1）y＝1+cosx；(2)y＝2cosx解(1).π2,0,2minmaxTyy(2).π2,2,2minmaxTyy例3不求值，比较下列各对余弦值的大小：52cos5cos)1(与57cos45cos)2(与1.余弦函数的图象以及“五点法”作图.2.余弦函数的性质.教材P66，练习第2、3题