圆周角和圆心角的关系第课时教学设计VIP免费

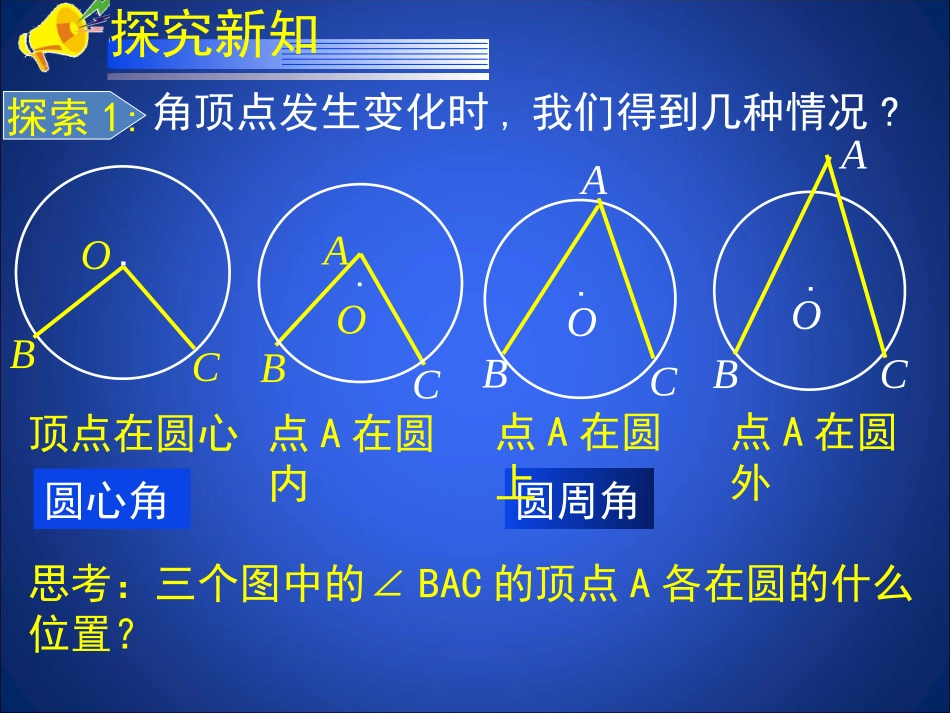
第三章圆3.4圆周角和圆心角的关系（第1课时）1.圆心角的定义?顶点在圆心的角叫圆心角2.圆心角的度数和它所对的弧的度数有何关系?如图：∠AOB弧AB的度数3.在同圆或等圆中，如果两个圆心角、两条、两条、两条________中有一组量相等，那么它们所对应的其余各组量都分别相等。弧弦=知识回顾弦心距角顶点发生变化时,我们得到几种情况?思考：三个图中的∠BAC的顶点A各在圆的什么位置？探索1:圆周角点A在圆内点A在圆外点A在圆上.OBCA.OBCAOBC顶点在圆心圆心角.AOBC.探究新知圆周角定义:顶点在圆上,并且两边分别与圆还有一个交点的角叫做圆周角..OBCA练习、指出图中的圆心角和圆周角圆心角：圆周角：∠AOB、∠AOC、∠BOC∠BAC,∠ABC,∠ACB●OBACBACBACBACBACBACBACDEDE问题提出：当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有什么关系.类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系？探索2:●OACB圆周角和圆心角的关系做一做：如图,∠AOB=80°，（1）请你画出几个所对的圆周角，这几个圆周角的大小有什么关系？教师提示:思考圆周角和圆心角有几种不同的位置关系？●OAB●OACB●OACBCAB⌒圆周角和圆心角的关系做一做：如图,∠AOB=80°（2）这些圆周角与圆心角∠AOB的大小有什么关系?议一议:改变圆心角∠A0B的度数，上述结论还成立吗？●OAB●OACB●OACBC圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.●OACB●OACB●OACB12ACBAOB即下面对定理进行演绎证明圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.●OACB●OACB●OACB已知：如图，∠ACB是所对的圆周角，∠AOB是所对的圆心角，求证：AB⌒AB⌒12ACBAOB先证明哪一种情况？1.首先考虑一种特殊情况：当圆心(O)在圆周角(∠ACB)的一边(BC)上时,圆周角∠ACB与圆心角∠AOB的大小关系. ∠AOB是△ACO的外角，∴∠AOB=∠C+∠A. OA=OC，∴∠A=∠C.∴∠AOB=2∠C.12ACBAOB即ACB●O2.当圆心(O)在圆周角(∠ACB)的内部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?老师提示:能否转化为1的情况?过点C作直径CD.由1可得:D●OACB11,22ACDAODBCDBOD12ACDBCDAODBOD12ACBAOB即3.当圆心(O)在圆周角(∠ACB)的外部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样?老师提示:能否也转化为1的情况?过点C作直径CD.由1可得:DACB●O11,22ACDAODBCDBOD12ACDBCDAODBOD12ACBAOB即OCABOCABOCAB化归化归分类讨论、转化DD方法小结●OBACBACBACBACBACBACBACDEDE问题回顾：当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角大小有什么关系?连接AO、CO,111,,,222ABCAOCADCAOCAECAOCABCADCAEC定理：同弧或等弧所对的圆周角相等.一、这节课主要学习了两个知识点：1、圆周角定义。2、圆周角定理及其定理应用。二、方法上主要学习了圆周角定理的证明，渗透了类比，“特殊到一般”的思想方法和分类讨论的思想方法。三、圆周角及圆周角定理的应用极其广泛，也是中考的一个重要考点，望同学们灵活运用。课堂小结1.如图，在⊙O中，∠BOC=50°，求∠BAC的大小BAC●O解：在⊙O中，∠BOC=50°0011502522BACBOC随堂练习2.如图，哪个角与∠BAC相等，你还能找到那些相等的角？CABD解：∠BAC=∠BDC∠ADB=∠ACB∠CAD=∠CBD∠ABD=∠ACD随堂练习1.如图，OA、OB、OC都是⊙O的直径，∠AOB=2∠BOC，∠ACB与∠BAC的大小有什么关系，为什么？OABC12112AOB122BOC又 ∠AOB=2∠BOC11122222AOBBOCBOC解：∠BAC=2∠ACB，理由:即∠BAC=2∠ACB习题讲解2.如图，A、B、C、D是⊙O上的四点，且∠BCD=100°，求∠BOD与∠BAD的大小o1802BADBODCOBDA解： ∠BCD=100°∴优弧所对的圆心角∠BOD=2∠BCD=200°∴劣弧所对的圆心角∠BOD=36O°-200°=160°习题讲解3.为什么...