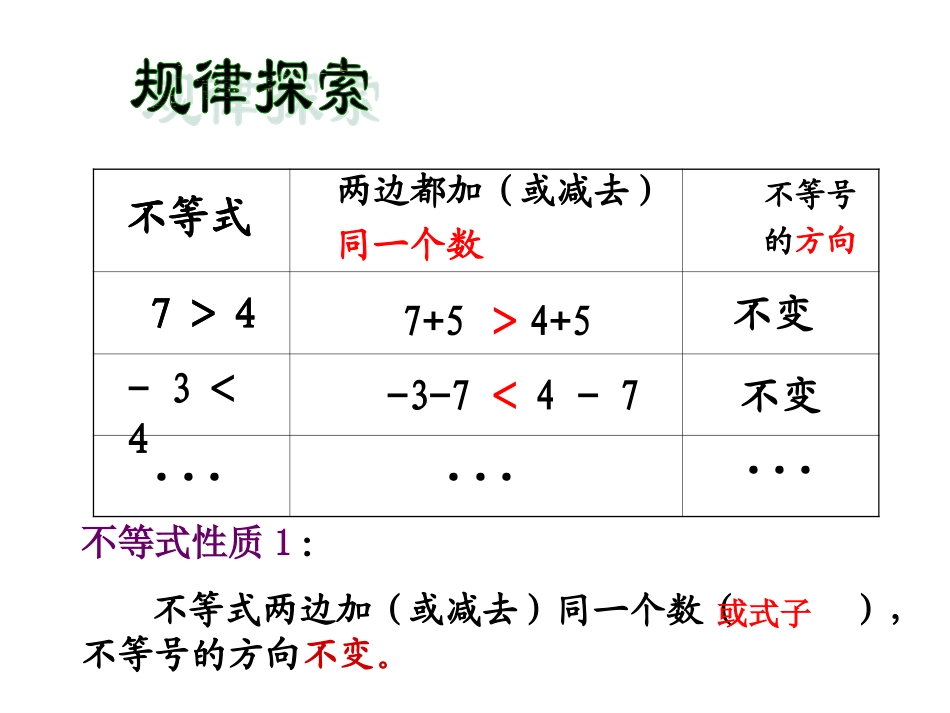
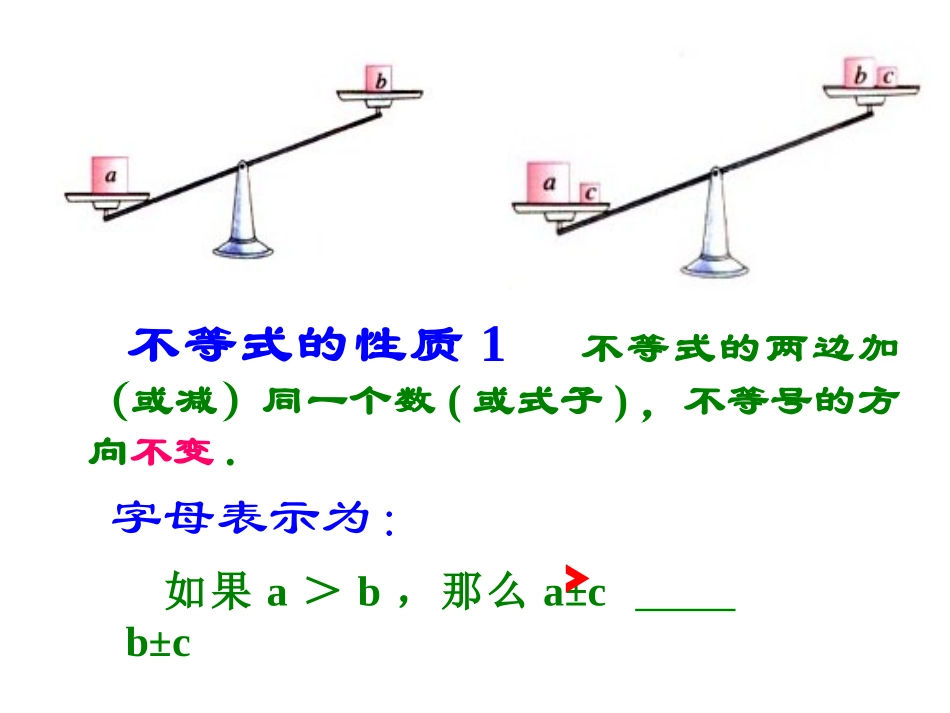
等式基本性质1:等式的两边都加上(或减去)同一个整式,等式仍旧成立等式基本性质2:等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立如果a=b,那么a±c=b±c如果a=b,那么ac=bc或(c≠0),cbca不等号的方向不等式7>4-3<47+54+5-3-74-7不变不变两边都加(或减去)同一个数不等式7>4.........不等式性质1:不等式两边加(或减去)同一个数(),不等号的方向不变。或式子><不等式的性质1不等式的两边加(或减)同一个数(或式子),不等号的方向不变.如果a>b,那么a±cb±c字母表示为:﹥不等号的方向不等式7>4-8<47×54×5-8÷24÷2不变不变两边都乘(或除以)同一个正数不等式7>4.........不等式性质2:不等式两边乘()同一个正数,不等号的方向不变。或除以><不等式的性质2不等式的两边乘(或除以)同一个正数,不等号的方向不变.如果a<b,c>0那么acbc,字母表示为:﹤).___(cbca或﹤不等号的方向不等式7>4-8<47×(-5)4×(-5)-8÷(-2)4÷(-2)改变改变两边都乘(或除以)同一个负数不等式7>4.........不等式性质3:不等式两边乘()同一个负数,不等号的方向改变。或除以<>不等式的性质3不等式的两边乘(或除以)同一个负数,不等号的方向改变必须把不等号的方向改变如果a>b,c<0那么acbc,字母表示为:类比推导﹤).___(cbca或﹤不等式性质1:不等式两边加(减去)同一个正数,不等号的方向不变。不等式性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变。不等式性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变。针对练习针对练习(1)如果x-5>4,那么两边都可得到x>9(2)如果在-7<8的两边都加上9可得到(3)如果在5>-2的两边都加上a+2可得到(4)如果在-3>-4的两边都乘以7可得到(5)如果在8>0的两边都乘以8可得到(6)如果在的两边都乘以14可得到X7>2+X2加上52<17a+7>a-21>-2864>02x>28+7x(1)如果在不等式8>0的两边都乘以―8可得到(2)如果-3x>9,那么两边都除以―3可得到(3)设m>n,用“>”或“<”填空:m-5n-5(根据不等式的性质)-6m-6n(根据不等式的性质)针对练习-64<0x<-3>1<3例1:判断下列各题的推导是否正确?为什么(学生口答)(1)因为7.5>5.7,所以-7.5<-5.7;(2)因为a+8>4,所以a>-4;(3)因为4a>4b,所以a>b;(4)因为-1>-2,所以-a-1>-a-2;(5)因为3>2,所以3a>2a.答:.(1)正确,根据不等式基本性质3.(2)正确,根据不等式基本性质1.(3)正确,根据不等式基本性质2.(4)正确,根据不等式基本性质1.(5)不对,应分情况逐一讨论.当a>0时,3a>2a.(不等式基本性质2)当a=0时,3a=2a.当a<0时,3a<2a.(不等式基本性质3)例2:设a>b,用“<”或“>”填空并口答是根据哪一条不等式基本性质。(1)a-3____b-3;(2)a÷3____b÷3(3)0.1a____0.1b;(4)-4a____-4b(5)2a+3____2b+3;(6)(m2+1)a____(m2+1)b(m为常数)>>>>><练习:已知a<0,用“<”或“>”号填空:(1)a+2____2;(2)a-1_____-1;(3)3a______0;(4)-a/4______0;(5)a2_____0;(6)a3______0(7)a-1______0;(8)|a|______0.答:(1)a+2<2,根据不等式基本性质1.(2)a-1<-1,根据不等式基本性质1.(3)3a<0,根据不等式基本性质2.(5)因为a<0,两边同乘以a<0,由不等式基本性质3,得a2>0.(6)因为a<0,两边同乘以a2>0,由不等式基本性质2,得a3<0.(7)因为a<0,两边同加上-1,由不等式基本性质1,得a-1<-1.又已知,-1<0,所以a-1<0.(8)因为a<0,所以a≠0,所以|a|>0.(4)-a/4>0,根据不等式基本性质3.(1)(2)(3)(4)(5)bbbaba33babababa22002aa33aa1、判断(√)(×)(√)(×)(×)2、判断正误:(1)如果a>b,那么ac>bc。(2)如果a>b,那么ac2>bc2。(3)如果ac2>bc2,那么a>b。××例3利用不等式的性质解下列不等式.(1)x-7>26(2)-4x3﹥(3)3x<2x+1Zx.xk•例1利用不等式的性质解下列不等式用数轴表示解集.•(1)x-7>264344x我是最棒的☞☞解:根据不等式性质1,得X-7+7>26+7X>33330(2)-4x3﹥解:根据不等式性质3,得X<―43解未知...