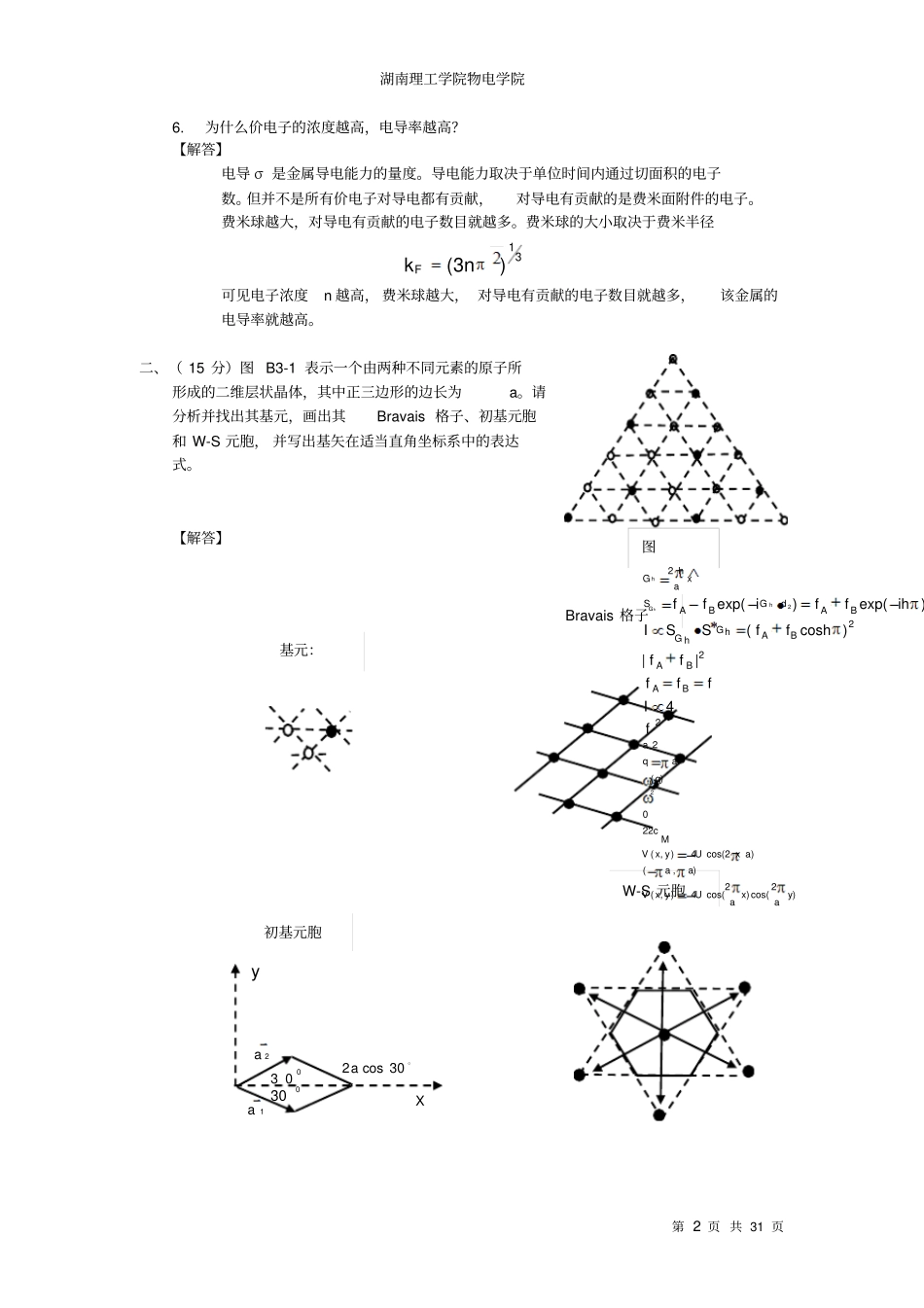
湖南理工学院物电学院第1页共31页固体物理测试卷(3)一、(6题,每题5分,共30分)简要回答下列问题:1.解释费米面(Ferimisurface)【解答】绝对零度下(T=0k),晶体中电子在k空间中占据态与未占据态的分界面。在非零温度下指电子占据几率为1/2的状态所构成的面。2.解释布里渊区和第一布里渊区(BrillourinZone,FirstBrillourinZone)【解答】在倒格子空间,以一格点为原点,此格子与其余格点连线的垂直平分面所围成的区域称为布里渊区。其中包含原点在内的最小封闭区域(WS原胞)为第一布里渊区,与第一布里渊区连通的区域(三维时面连通,二维时线连通)为第二布里渊区。3.试用能带论简述导体、绝缘体、半导体中电子在能带中填充的特点。【解答】金属或导体中的价电子没有把价带(最高填充带)填满,此为导带。绝缘体中的价电子正好把价带填满,且更高的许可带(空带)与价带间相隔较宽的禁带。半导体和绝缘体相似,但禁带较窄。4.解释朗道能级(Landanlevel)【解答】在垂直与恒定磁场的平面内,电子的圆周运动对应于以一种简谐运动,其能量是量子化的:cvv21((v=1,2,3...........)meBc这些量子化的能级称为朗道能级。5.长光学支格波与长声学支格波本质上有何区别?【解答】长光学支格波的特征是每个原胞内的不同原子做相对振动,振动频率较高,它包含了晶格振动频率最高的振动模式。长声学支格波的特征是原胞内的不同原子没有相对位移,原胞做整体运动,振动频率较低,它包含了晶格振动频率最低的振动模式,波速是一常数。任何晶体都存在声学支格波,但见到晶格(非复式格子)晶体不存在光学支格波。湖南理工学院物电学院第2页共31页6.为什么价电子的浓度越高,电导率越高?【解答】电导σ是金属导电能力的量度。导电能力取决于单位时间内通过切面积的电子数。但并不是所有价电子对导电都有贡献,对导电有贡献的是费米面附件的电子。费米球越大,对导电有贡献的电子数目就越多。费米球的大小取决于费米半径31)3(nkF可见电子浓度n越高,费米球越大,对导电有贡献的电子数目就越多,该金属的电导率就越高。二、(15分)图B3-1表示一个由两种不同元素的原子所形成的二维层状晶体,其中正三边形的边长为a。请分析并找出其基元,画出其Bravais格子、初基元胞和W-S元胞,并写出基矢在适当直角坐标系中的表达式。【解答】图)2cos()2cos(4),(),()2cos(4),(220)(2222hh222hh4||)cosh()exp()exp(hyaxaUyxVaaaxUyxVMcqaqaBABABAGGBAdGBASxahGfIfffffffSSIihffiffG基元:Bravais格子。30cos2a2a0300301ayX初基元胞W-S元胞湖南理工学院物电学院第3页共31页基矢:yxyxeaeaeaeaa232330cos230sin30cos2)30(cos00002!!!注意:从第三.1题和第三.2题中选做其中一个题三、1(10分)He3原子是具有自旋1/2的费米子。在绝对零度附件,液体He3的密度为3081.0cmg。计算费米能量F和费米温度FT。He3原子的质量为gm24105。【解答】He3的自旋为1/2,是费米子,其质量gm24105。在密度3081.0cmg的液体He3中,单位体积中的He3数目为:3283221062.11062.1mcmmn其费米能为:32222322nmmkFF将n,m值带入;得到:JF23108.6其费米温度为:KKkTBFF9.41038.1108.62323三.2(10分)求出bccBravais格子(110)晶面族的晶面上的格点数密度和面距离。【解答】晶面格点数面密度面距离bccbcc{100}21a2a四、(15分)考虑晶格常数为a和c的三维简单六角晶体的第一布里渊区。令cG为平行于晶湖南理工学院物电学院第4页共31页格c轴的最短倒格矢。(1)证明对于六角密堆积结构,晶体势场rV的傅里叶分量cGV为零。(2)cGV是否也为零?(3)为什么二价原子构成的简单六角晶格在原则上有可能是绝缘体?(4)为什么不可能得到由单价原子六角密堆积形成的绝缘体?【解答】(1)证:由教材p61(3.2.30)和(3.2.31)两式,对于基元中原子数p>1的复式晶格,且由同种原子组成的基元,有:jjhGdGifSh)exp(①fSGVGVhGhh)(1②其中:cGV是复式晶格的某一倒格矢hG的傅里叶分量。hGS是同种原子组成的基元的几何结构因子。由②式可知,对于复式晶格的某一倒格矢hG,如结构因子为零,则周期势rV相应的傅里叶分量也为零。因此,来计算对于六角密堆...