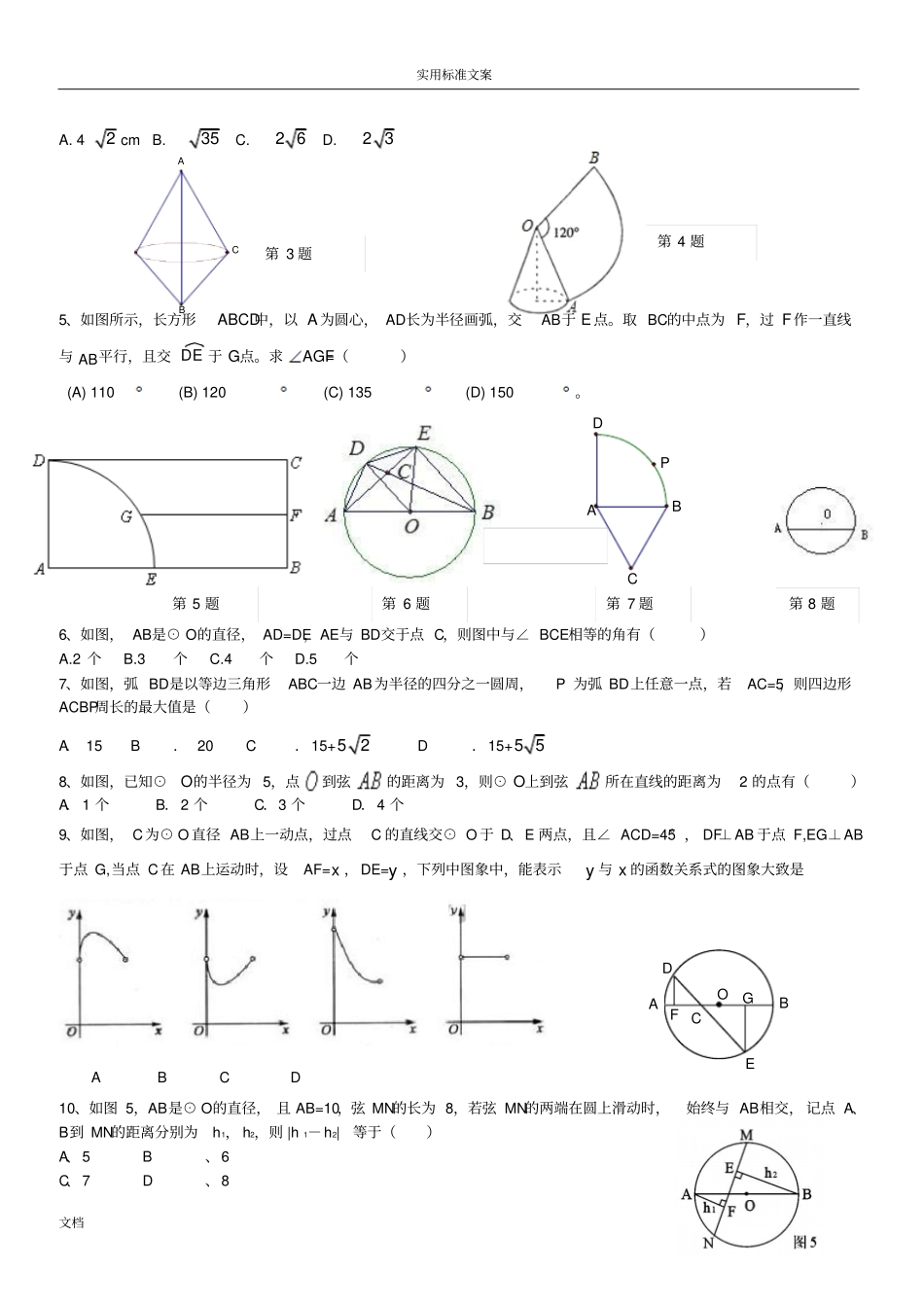
实用标准文案文档第三章《圆的基本性质》的知识点及典型例题知识框图1、过一点可作个圆。过两点可作个圆,以这两点之间的线段的上任意一点为圆心即可。过三点可作个圆。过四点可作个圆。2、垂径定理:垂直于弦的直径,并且平分垂径定理的逆定理1:平分弦()的直径垂直于弦,并且平分垂径定理的逆定理2:平分弧的直径3、圆心角定理:在同圆或等圆中,相等的圆心角所对的,所对的圆心角定理的逆定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么都相等。注解:在由“弦相等,得出弧相等”或由“弦心距相等,得出弧相等”时,这里的“弧相等”是指对应的劣弧与劣弧相等,优弧与优弧相等。在题目中,若让你求⌒AB,那么所求的是弧长4、圆周角定理:一条弧所对的圆周角等于它所对的圆概念圆、圆心、半径、直径弧、弦、弦心距、等弧圆心角、圆周角三角形的外接圆、三角形的外心、圆的内接三角形圆的基本性质圆周角定理及2个推论圆的相关计算弧可分为劣弧、半圆、优弧在同圆或等圆中,能够重合的两条弧叫等弧点和圆的位置关系不在同一直线上的三点确定一个圆圆的轴对称性垂径定理及其2个逆定理圆的中心对称性和旋转不变性圆心角定理及逆定理求半径、弦长、弦心距求圆心角、圆周角、弧长、扇形的面积、圆锥的侧面积及表面积圆的相关证明求不规则阴影部分的面积证明线段长度之间的数量关系;证明角度之间的数量关系证明弧度之间的数量关系;证明多边形的形状;证明两线垂直圆心角定理及逆定理都是根据圆的旋转不变性推出来的三角形的外心到三角形三个顶点的距离相等实用标准文案文档圆周角定理推论1:半圆(或直径)所对的圆周角是;90°的圆周角所对的弦是圆周角定理推论2:在同圆或等圆中,所对的圆周角相等;相等的圆周角所对的也相等5、拓展一下:圆内接四边形的对角之和为6、弧长公式:在半径为R的圆中,n°的圆心角所对的弧长l的计算公式为l=7、扇形面积公式1:半径为R,圆心角为n°的扇形面积为。这里面涉及3个变量:,已知其中任意两个,都可以求出第3个变量。我们中需要记住一个公式即可。扇形面积公式2:半径为R,弧长为l的扇形面积为8、沿圆锥的母线把圆锥剪开并展平,可得圆锥的侧面展开图是一个,圆锥的侧面积等于这个扇形的面积,其半径等于圆锥的,弧长等于圆锥的9、圆锥的侧面积:;圆锥的全面积:10、圆锥的母线长l,高h,底面圆半径r满足关系式11、已知圆锥的底面圆半径r和母线长l,那么圆锥的侧面展开图的圆心角为12、圆锥的侧面展开图的圆心角x的取值范围为考点一、与圆相关的命题的说法正确的个数,绝大多数是选择题,也有少部分是填空题(填序号)考点二、求旋转图形中某一点移动的距离,这就要利用弧长公式考点三、求半径、弦长、弦心距,这就要利用勾股定理和垂径定理及逆定理考点四、求圆心角、圆周角考点五、求阴影部分的面积考点六、证明线段、角度、弧度之间的数量关系;证明多边形的具体形状考点七、利用不在同一直线上的三点确定一个圆的作图题考点八、方案设计题,求最大扇形面积考点九、将圆锥展开,求最近距离练习一、选择题1、下列命题中:①任意三点确定一个圆;②圆的两条平行弦所夹的弧相等;③任意一个三角形有且仅有一个外接圆;④平分弦的直径垂直于弦;⑤直径是圆中最长的弦,半径不是弦。正确的个数是()A.2个B.3个C.4个D.5个2、如图,AB是半圆O的直径,点P从点O出发,沿OAABBO的路径运动一周.设OP为s,运动时间为t,则下列图形能大致地刻画s与t之间关系的是()3、如图所示,在△ABC中,∠BAC=30°,AC=2a,BC=b,以AB所在直线为轴旋转一周得到一个几何体,则这个几何体的全面积是()A.2πaB.πabC.3πa2+πabD.πa(2a+b)4、如图,有一圆心角为120°,半径长为6cm的扇形,若将OA、OB重合后围成一圆锥侧面,那么圆锥的高是()PAOBstOsOtOstOstA.B.C.D.实用标准文案文档GEDACFOBA.42cmB.35C.26D.235、如图所示,长方形ABCD中,以A为圆心,AD长为半径画弧,交AB于E点。取BC的中点为F,过F作一直线与AB平行,且交DE于G点。求AGF=()(A)110(B)120(C)135(D)150。6、如图,AB是⊙O的直径,AD=DE,AE...