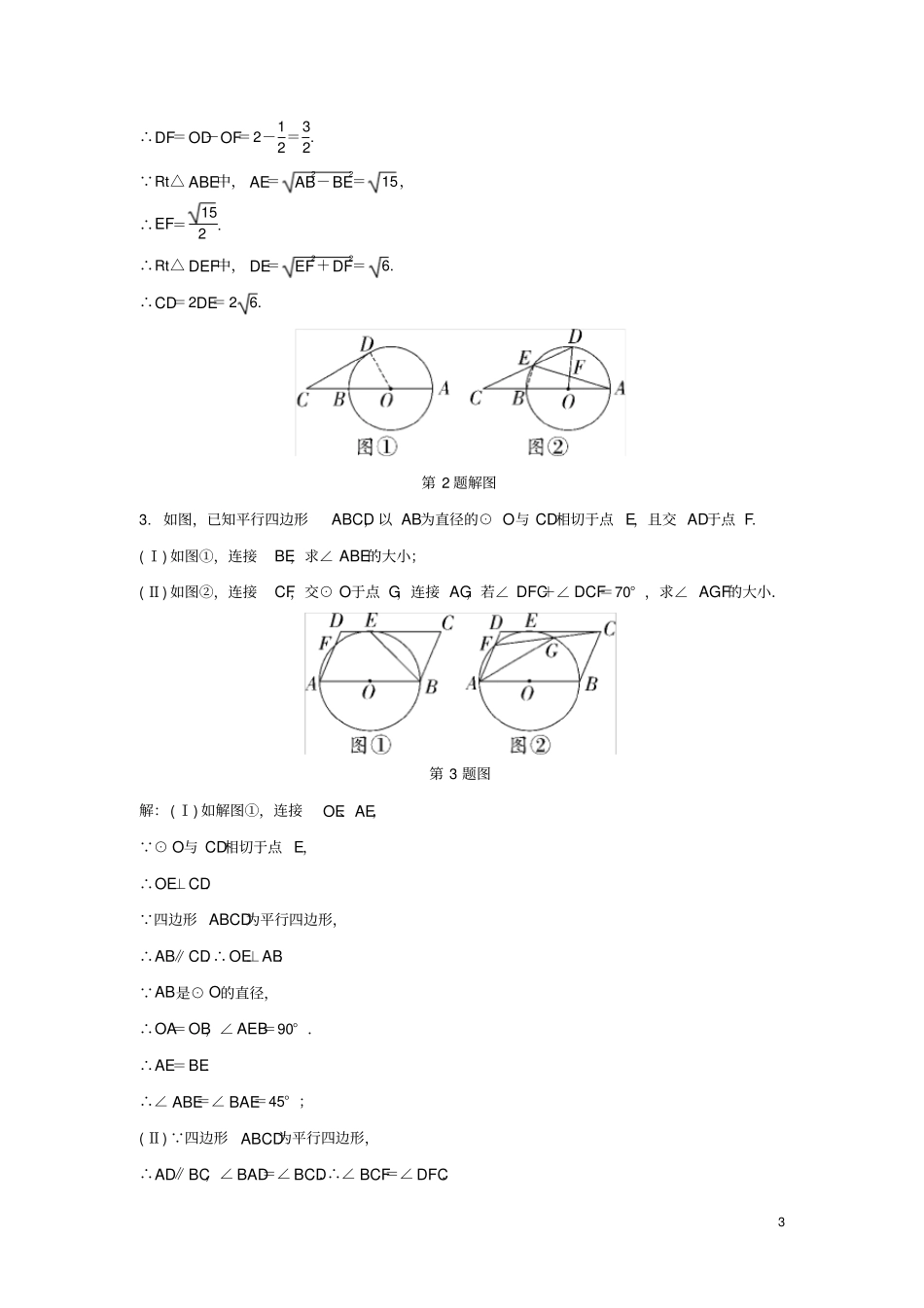
1与圆有关的证明与计算1.在△ABC中,∠ABC=45°,∠C=60°,⊙O经过点A、B,与BC交于点D,连接AD.(Ⅰ)如图①,若AB是⊙O的直径,交AC于点E,连接DE,求∠ADE的大小.(Ⅱ)如图②,若⊙O与AC相切,求∠ADC的大小.第1题图解:(Ⅰ)如解图①,连接BE, ∠ABC=45°,∠C=60°,∴∠BAC=75°. AB是⊙O的直径,∴∠AEB=90°.∴∠ABE=∠AEB-∠BAC=15°. ∠ABE=∠ADE,∴∠ADE=15°;(Ⅱ)如解图②,连接OA,OD, AC是⊙O的切线,∴∠OAC=90°. ∠ABC=45°,∴∠AOD=90°. OA=OD,∴∠OAD=45°.∴∠DAC=∠OAC-∠OAD=45°. ∠C=60°,∴∠ADC=75°.2第1题解图2.如图,AB是⊙O的直径,且AB=4,点C在AB延长线上,且BC=2,点D是⊙O上一点,连接CD.(Ⅰ)如图①,若CD与⊙O相切,求CD的长;(Ⅱ)如图②,若CD与⊙O的另一个交点为点E,且E为CD的中点,连接OD、AE交于点F,求CD的长.第2题图解:(Ⅰ)如解图①,连接OD, CD与⊙O相切,∴OD⊥CD,即∠ODC=90°.又 AB是⊙O的直径,且AB=4,BC=2,∴OD=OB=OA=2,OC=4.∴Rt△COD中,CD=42-22=23;(Ⅱ)如解图②,连接BE, AB是⊙O的直径,∴∠AEB=90°. 点E为CD的中点,BC=OB=OD=2,∴BE∥OD,BE=12OD=1.∴∠AFO=∠AEB=90°.∴OD⊥AE,AF=EF.又 O是AB的中点,∴OF=12BE=12.3∴DF=OD-OF=2-12=32. Rt△ABE中,AE=AB2-BE2=15,∴EF=152.∴Rt△DEF中,DE=EF2+DF2=6.∴CD=2DE=26.第2题解图3.如图,已知平行四边形ABCD,以AB为直径的⊙O与CD相切于点E,且交AD于点F.(Ⅰ)如图①,连接BE,求∠ABE的大小;(Ⅱ)如图②,连接CF,交⊙O于点G,连接AG,若∠DFC+∠DCF=70°,求∠AGF的大小.第3题图解:(Ⅰ)如解图①,连接OE、AE, ⊙O与CD相切于点E,∴OE⊥CD. 四边形ABCD为平行四边形,∴AB∥CD.∴OE⊥AB. AB是⊙O的直径,∴OA=OB,∠AEB=90°.∴AE=BE.∴∠ABE=∠BAE=45°;(Ⅱ) 四边形ABCD为平行四边形,∴AD∥BC,∠BAD=∠BCD.∴∠BCF=∠DFC.4 ∠DFC+∠DCF=70°,∴∠BCF+∠DCF=70°.∴∠BCD=70°.∴∠BAD=70°.如解图②,连接BF, AB是⊙O的直径,∴∠AFB=90°.∴∠ABF=90°-70°=20°.∴∠AGF=∠ABF=20°.第3题解图4.已知AB是⊙O的弦,C是劣弧AB︵的中点,D是⊙O上一点,CD交AB于点E,点P为BA的延长线上一点,PD=PE.(Ⅰ)如图①,求证:PD是⊙O的切线;(Ⅱ)如图②,当AB为⊙O的直径时,连接BC,若tan∠BCD=2,求tan∠APD的值.第4题图(Ⅰ)证明:如解图①,连接OC、OD, 点C是劣弧AB︵的中点,∴OC⊥AB. OC=OD,∴∠OCD=∠ODC. PD=PE,∴∠PDE=∠PED.又 ∠PED=∠CEB,∠CEB+∠OCD=90°,5∴∠PDE+∠ODC=90°,即∠PDO=90°. OD是⊙O的半径,∴PD是⊙O的切线;(Ⅱ)解:如解图②,连接AD、OD、BD, AB是⊙O的直径,∴∠ADB=90°. ∠BAD=∠BCD,∴tan∠BAD=BDAD=tan∠BCD=2. PD是⊙O的切线,∴∠ODP=90°.∴∠PBD=∠ADP,又 ∠P=∠P,∴△APD∽△DPB.∴PAPD=PDPB=ADDB=12.设PA=a,则PD=2a,PB=4a,则AB=3a,∴OD=32a.∴tan∠APD=ODPD=34.图①图②第4题解图5.已知BC是⊙O的直径,AD是⊙O的切线,切点为A,AD交CB的延长线于点D,连接AB,AO.(Ⅰ)如图①,求证:∠OAC=∠DAB;(Ⅱ)如图②,若AD=AC,E是⊙O上一点,连接AE、BE,求∠E的大小.6第5题图(Ⅰ)证明: AD是⊙O的切线,切点为A,∴DA⊥AO.∴∠DAO=90°.∴∠DAB+∠BAO=90°. BC是⊙O的直径,∴∠BAC=90°.∴∠BAO+∠OAC=90°.∴∠OAC=∠DAB;(Ⅱ)解: OA=OC,∴∠OAC=∠C. AD=AC,∴∠D=∠C.∴∠OAC=∠D. ∠OAC=∠DAB,∴∠DAB=∠D. ∠ABC=∠D+∠DAB,∴∠ABC=2∠D. ∠D=∠C,∴∠ABC=2∠C. ∠BAC=90°,∴∠ABC+∠C=90°.∴2∠C+∠C=90°.∴∠C=30°.∴∠E=∠C=30°.6.已知?ABCD的边AD与经过A、B、C三点的⊙O相切于点A.(Ⅰ)如图①,连接AC,若∠D=32°,求∠ACD的大小;(Ⅱ)如图②,延长DC交⊙O于点E,连接BE,若sin∠E=1213,⊙O的半径为13,求BC的长.7第6题图(Ⅰ)如解图①,连接OA, AD与⊙O相切于点A,∴OA⊥AD. 四边形ABC...