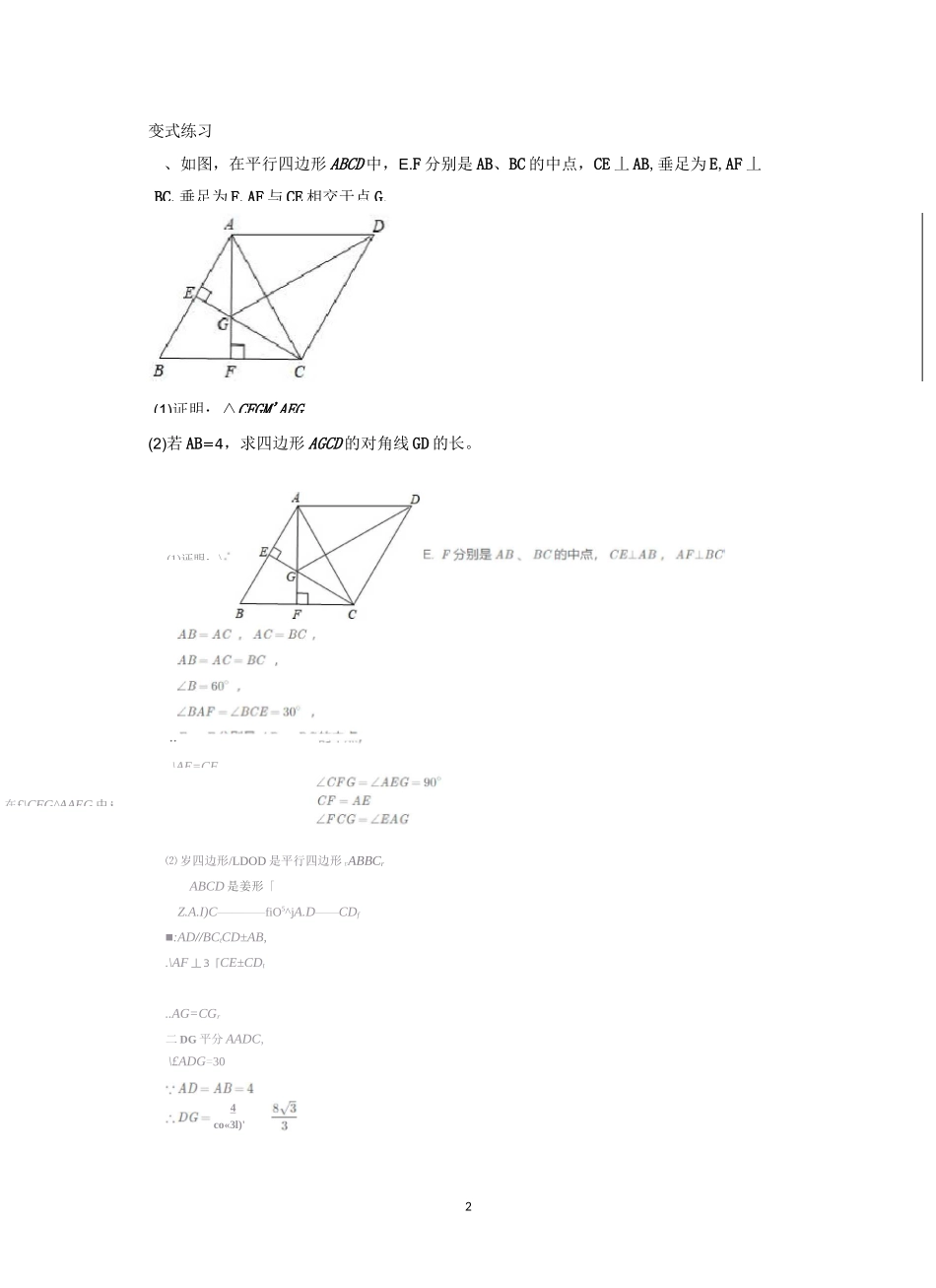
1平行四边形与特殊平行四边形(专题与提升)一、平行四边形的性质(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;例、如图,在口ABCD中,各内角的平分线分别相交于点E,F,G,H.(1)求证:△ABG^^CDE;(3)若AB=6,BC=4,ZDAB=60。,求四边形EFGH的面积。\ZGAB=-ABAD.£GBA=-AABC,\^BAG=ADCE,同理可得.£DEC=^\£AHD=9(1^EIIG二四边形EFGH是矩形;⑶依题意得丄D4G-£BAD3(1..A4BG^CDEIASA);⑵四WJf?EFGII是矩形*-/BAD.^DCE-/DCBT在ixABG和中,^BAG=ADCEABCD£ABGZCDE■^GAB+AGBA=(!}■/GAtEC^^BCD,-ABCDi=P.ZDAB+£ABC=18(r,[1DAB+ZABC)r--ABCD中,ABAD=£DCB,同理可得』£ABG=^CDEr@P£AGB=9(rr…迟、F分别是及7的中原'2变式练习(2)若AB=4,求四边形AGCD的对角线GD的长。⑵岁四边形/LDOD是平行四边形rABBCrABCD是姜形「Z.A.I)C————fiO5^jA.D——CDf■:AD//BCtCD±AB,.\AF丄3「CE±CDt..AG=CGr二DG平分AADC,、如图,在平行四边形ABCD中,E.F分别是AB、BC的中点,CE丄AB,垂足为E,AF丄BC,垂足为F,AF与CE相交于点G.(1)证明:△CFGM'AEG..\AE=CFr在£\CFG^AAEG中i(1)证明:\\£ADG=304co«3l)'3、如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.1⑴求证:"=90。—2ZC;(2)当ZC=90。,ND=NP时,判断线段MP与AM的数量关系,并给予证明。(1)证明:过点迟作迟卩丄PD于点过点D^DGLBP于庶心与交于点-BD=BN=DMt二EF与DG是^DBN、的平分线r二由四边形内角和为:卿,可得"一劲TG1SO!r^DIIB=朗(P-[ZGDB-ZFBD}=1S(J-+(ISO-ADAB)=9沪-ADAB,/.ZDIIB=ZFHG=1^-£P=9II'+1ACS理由:过点P作于点庆PR^BC于点叭当ZC=911°时,则^DPB=45"rBN//CD,/.^BND=£BDN=£SDNt同理:£PEDfPERr作PK丄砂于点心在厶PKD和△PSD中「(£S=£PKD=^JZPDS=^PDKf[PD=PD.\/\PKD^^PSD(AAS)r同理:APi?Z?f..PS=PRt/.四边形刖蚀是正方形,延长M交Qg于点4则Q为用的中点『QS=PQ=xf^^5=CS=RC=2ztHB=DB=x,设SD=pifBD=x—mf则(T+m)2=x-—{2x—m)'r/.m:i=2:t/.PB=v<5i,PM=I,AM=|xr/.A/P:AAf=⑷:込/.zp=9(r-lzc;(2)MP:AM=声:2、SDCAD=EFAD=EF(2)求证:四边形ADFE是平行四边形。证明:("…△止右?是等边三活形,.^AEF=^ZAEB=^\AE=-.^ACB=^\£BAC=^'.^AEF=ZBACf£EFA=ZACB「在△KEF和ABAC中ZEFA=ZACH^AEF^ABAG,(2\-:^ACD是等边三用\AC=AD,£DAC=^由(1)的结论厚且CEFr-,-iLBAC=^PAD=IBAC-£DAC=站沪-,-^EFA三四边形ADFE是平行四边形.£AEF=£BAC4二、平行四边形的判定例、如图,分别以Rt^ABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知ZBAC=30°,EF丄AB于点F,连接DF.⑴求证:AC=EF;5变式练习、如图,"BC为等边三角形,D.F分别为EC、上的点,且CD=BF.(1)求证:^ACD^CBF;(2)以4D为边作等边三角形"DE,点D在线段EC上的何处时,四边形CDEF是平行四边形。⑴证明:"ARC%等边三角形,tAC=BC,在"CD和鸣<7石砂\AC=BCCD=bb:.^ACD^CBF(SAS);(2)D在BO的中点时,四边形CD血是爭亍四边形,D是EC中点「•F是加?中点「..AD丄矽7”CF±A8「二EFCHM别严,ABAD=^}J又也是等边三角形’:.DEwCFt又CF=ACE•四边形是平行四边形。6、如图,在平面直角坐标系xOy,直线y=x+l与y=-2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由。①如下图:当0E//时,所収直皴0E的解析式为y-2xf联立0E、ABt得联立0以g得'解得2即因解得,y=x-l①y=_2工②(112二设直线DE的解析式为yH4将.点D的坐标代入直线的解析式彳异:y2x-~1,5联立DE、的得「一直线0D的解析式为射GNDEC交BA的延长线于点G,若AB=DC=2,ZFEC=45°,求FE的长度。门)证明:连接也儿取0卫的中点IT连接因FII.m分别是貝Da的中点,=ZHEFr:=UIFErHE=FII(\LIIEF=£IIFE:.£BME£CNE;\^1IEF=£IIFE=A^\EP:.EH”AB.Eli=i■:Ft卫分别是BCt的中点「FII//CD.FIICDr7三、三角形中位线定理例、⑴如图1,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:ZBME=ZCNE;(提示:取BD的中点H,...