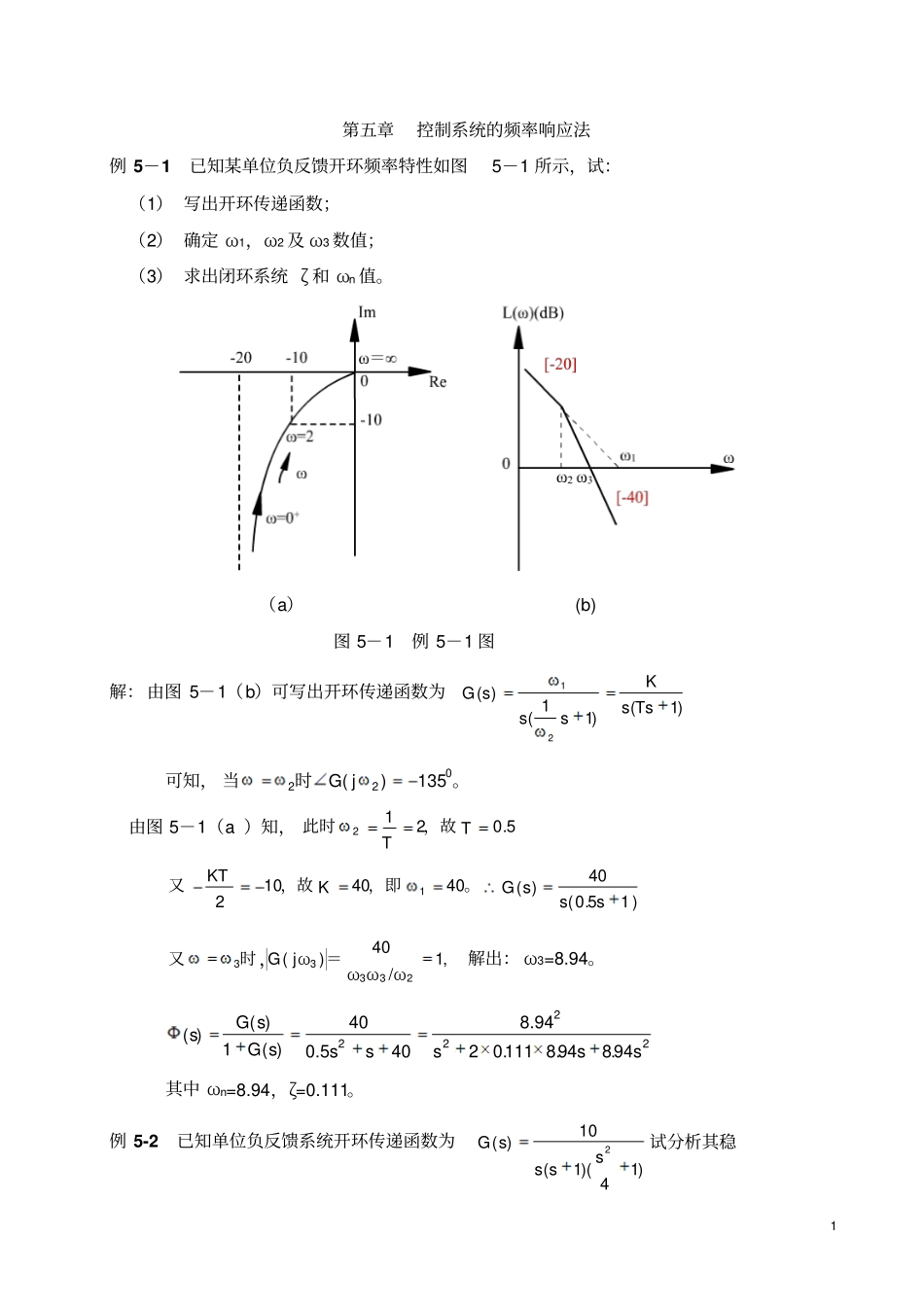
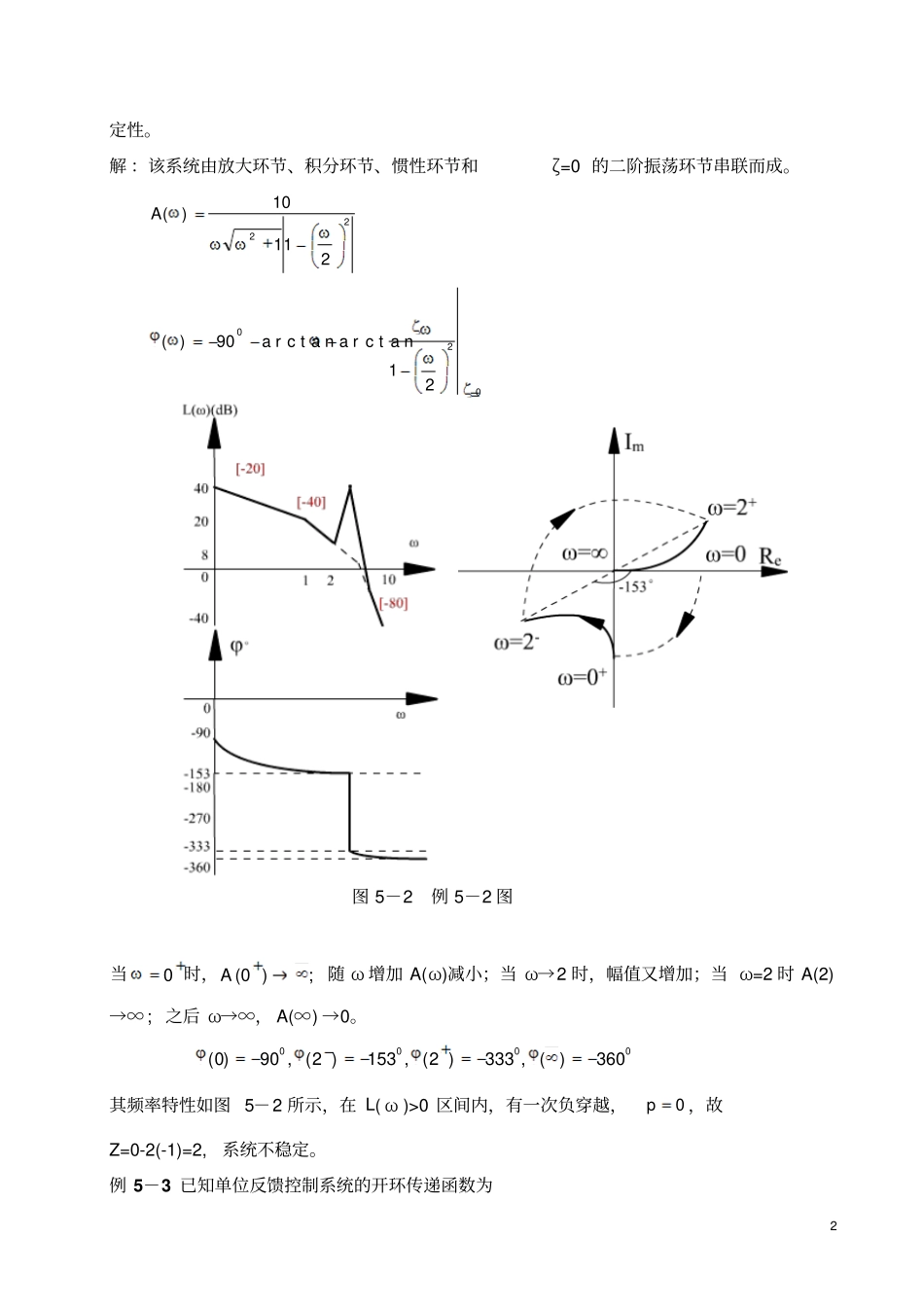
1第五章控制系统的频率响应法例5-1已知某单位负反馈开环频率特性如图5-1所示,试:(1)写出开环传递函数;(2)确定ω1,ω2及ω3数值;(3)求出闭环系统ζ和ωn值。(a)(b)图5-1例5-1图解:由图5-1(b)可写出开环传递函数为)1()11()(21TssKsssG可知,。时当022135)(jG由图5-1(a)知,5.0212TT,故此时。,即,故又40401021KKT)s.s(sG15040)(,140)(23333/ωωωjωG,=时又解出:ω3=8.94。22229489481110294.8405.040)(1)()s(s.s..ssssGsG其中ωn=8.94,ζ=0.111。例5-2已知单位负反馈系统开环传递函数为)14)(1(10)(2ssssG试分析其稳2定性。解:该系统由放大环节、积分环节、惯性环节和ζ=0的二阶振荡环节串联而成。2221110)(A02021arctanarctan90)(图5-2例5-2图;)0(A0时,当随ω增加A(ω)减小;当ω→2时,幅值又增加;当ω=2时A(2)→∞;之后ω→∞,A(∞)→0。0000360)(,333)2(,153)2(,90)0(其频率特性如图5-2所示,在L(ω)>0区间内,有一次负穿越,0p,故Z=0-2(-1)=2,系统不稳定。例5-3已知单位反馈控制系统的开环传递函数为3)1)(5)(2()(1sssKsG试画出系统的极坐标频率特性曲线并确定系统稳定性条件。解:)1)(151)(121(52)1)(5)(2()(11sssKsssKsG)1)(1)(1(321sTsTsTK式中,。=sTsTsTKK1,2.051,5.021,103211)1)(1)(1()321ωjTωjTωjTKG(jω)1)(1)(1()1)(1)(1(223222221321ωTωTωTωjTωjTωjTK))(1)(1(1(]1)[(22322122123213212323121TTTKTTTTTTjTTTTTTK)))(1)(1(1]1)[()(2232212212323121TTTTTTTTTKP))(1)(1(1()(2232212212321321TTTTTTTTTKQ)223222221111)(TTTKA3021arctan180arctanarctan)(TTT时,当12323121TTTTTT0)(1323121PTTTTTT时,即当时时,即当当32121323213210TTTTTTTTTTTT,Q(ω)=0。,,,,本例6.012.05.0323121321TTTTTTTTT所以ω在实数范围内,不存在P(ω)=0。4,3321213时当TTTTTT,375.0)3(,0)3(KPQ0180)3(,375.0)3(KA;-180(0),00,)0(,000K)A(QK)P(时,当。时,当0-270)(0,)(A0,)(,0)(QP图5-3例5-3图系统的开环幅相频率特性如图5-3所示。作出其镜像(图中虚线),从图中可以看出,要使系统稳定,G(jω)及其镜像应逆时针包围(-1,j0)点一圈,即(-1,j0)点应落在负实轴(-K,-0.375K)段。因此,系统稳定条件:K>1和0.375K<1,即1