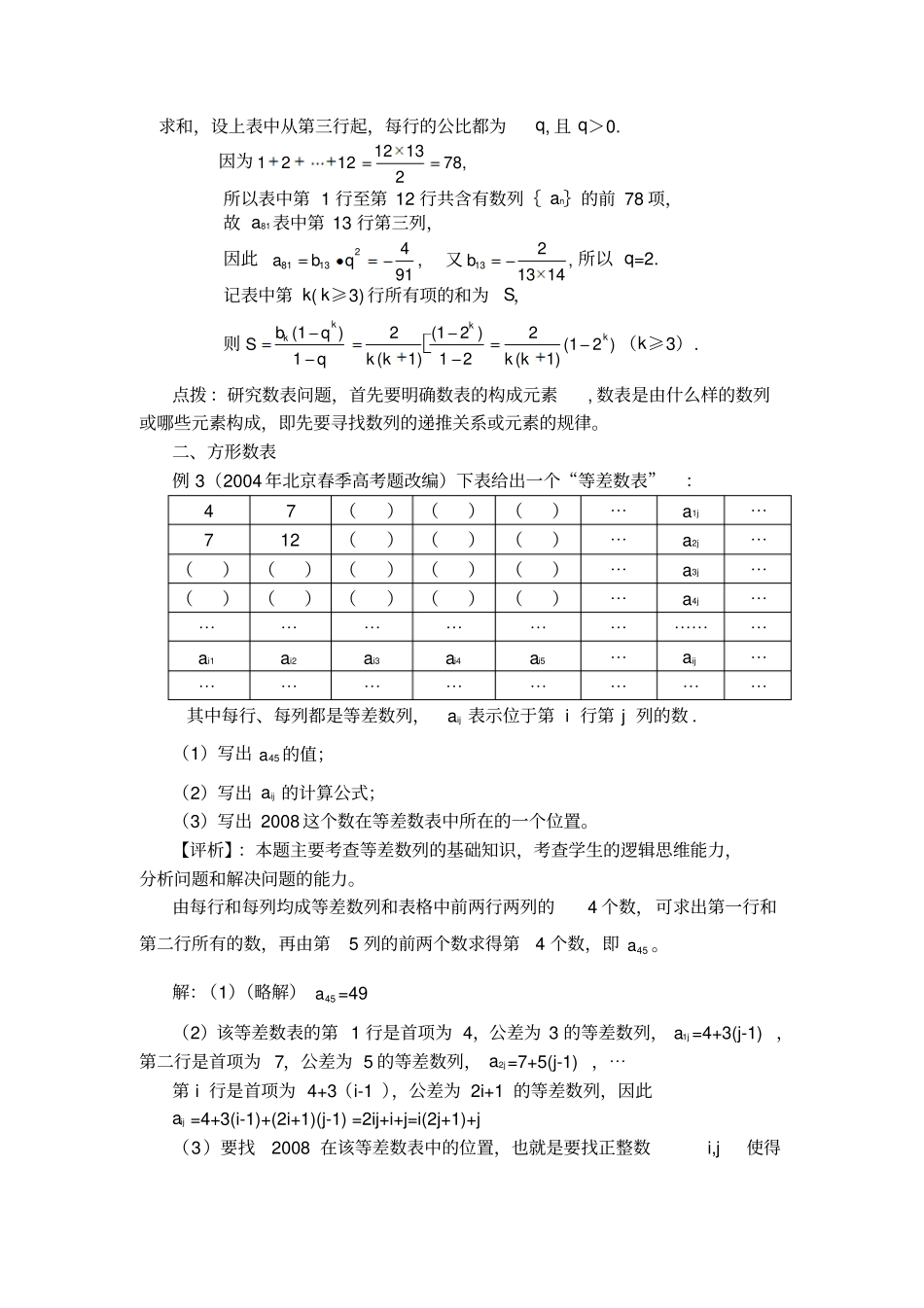
数列创新题型突破-------五、数阵和数表所谓数表就是指满足一定的生成规则并按一定的顺序排列成的一个表,数表问题常与数列知识联手,在高考中奏出一曲曲优美的“乐章”,逐渐成为高考命题的热门,本文试就数表问题考查的几种常见类型及变化趋势作一阐述,以馈读者。一、三角形数表例1(2008年江苏卷10)将全体正整数排成一个三角形数表:12345678910.......按照以上排列的规律,第n行(n≥3)从左向右的第3个数为.【评析】:通过列举、分析、归纳、猜想,前n-1行共有1+2+3+⋯+n-1个数,即共有22nn个,因此第n行第3个数是全体正整数中第22nn+3个数,即262nn例2(2008年山东卷19)将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:a1a2a3a4a5a6a7a8a9a10.......记表中的第一列数a1,a2,a4,a7,⋯构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足22nnnnSSbb=1(n≥2).(Ⅰ)证明数列{nS1}成等差数列,并求数列{bn}的通项公式;(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当91481a时,求上表中第k(k≥3)行所有项和的和.(Ⅰ)证明略,2,)1(21,1nnnnbn(Ⅱ)析:本题关键在于确定81a在表中的位置,再由通项公式求出q,然后求和,设上表中从第三行起,每行的公比都为q,且q>0.因为1213121278,2所以表中第1行至第12行共含有数列{an}的前78项,故a81表中第13行第三列,因此28113491abq,又132,1314b所以q=2.记表中第k(k≥3)行所有项的和为S,则(1)2(12)2(12)1(1)12(1)kkkkbqSqkkkk(k≥3).点拨:研究数表问题,首先要明确数表的构成元素,数表是由什么样的数列或哪些元素构成,即先要寻找数列的递推关系或元素的规律。二、方形数表例3(2004年北京春季高考题改编)下表给出一个“等差数表”:47()()()⋯a1j⋯712()()()⋯a2j⋯()()()()()⋯a3j⋯()()()()()⋯a4j⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ai1ai2ai3ai4ai5⋯aij⋯⋯⋯⋯⋯⋯⋯⋯⋯其中每行、每列都是等差数列,aij表示位于第i行第j列的数.(1)写出45a的值;(2)写出aij的计算公式;(3)写出2008这个数在等差数表中所在的一个位置。【评析】:本题主要考查等差数列的基础知识,考查学生的逻辑思维能力,分析问题和解决问题的能力。由每行和每列均成等差数列和表格中前两行两列的4个数,可求出第一行和第二行所有的数,再由第5列的前两个数求得第4个数,即45a。解:(1)(略解)45a=49(2)该等差数表的第1行是首项为4,公差为3的等差数列,a1j=4+3(j-1),第二行是首项为7,公差为5的等差数列,a2j=7+5(j-1),⋯第i行是首项为4+3(i-1),公差为2i+1的等差数列,因此aij=4+3(i-1)+(2i+1)(j-1)=2ij+i+j=i(2j+1)+j(3)要找2008在该等差数表中的位置,也就是要找正整数i,j使得2ij+i+j=2008,所以122008iij,当i=1时,得j=669所以,2008在等差数表中的一个位置是第1行第669列。点拨:对于数表形等差、等比数列的综合问题,行、列关系较为复杂,在解题时一定要多找等量关系,少设变量,尽可能把已知元素的值化归到同行或者同列。三、回形数表例4(2008江苏高考零距离突破二轮复习题)将自然数排成如下的螺旋状第一个拐弯处的数是2,第二个拐弯处的数是3,第20个及第25个拐弯处的数分别是,【评析】:由图可知,前n个拐弯处的数依次是2,3,5,7,10,13,17,21,26,⋯,①这是一个数列题目,要求找出它的第20项和第25项各是多少,因此要找出这个数列的规则,经观察,该数列的后一项减去一项,得一新数列1,2,2,3,3,4,4,5,5,⋯⋯②,把数列①的第一项添在数列②的前面得2,1,2,2,3,3,4,4,5,5,⋯⋯③,观察数列①,③发现原数列①的第n项na就等于数列③的前n项和,即21a,3122a,722123a,⋯,故第20个拐弯处的数a20=2+1+2+2+⋯+10+10=1+2(1+2+⋯+10)=111a25=2+1+2+2+⋯+12+12+13=170解法2:设第i个拐弯处的数为ai,显然a1=2,a2i=a2i-1+I,a2i+1=a2i+(i+1) 20=2×1025=2×12+1∴a20=1+2(1+2+⋯+10)=11a25=1+2(1+2+⋯+12)+13=170解法1到解法2由具体到抽象,体现出思维不断优化的过程。点...