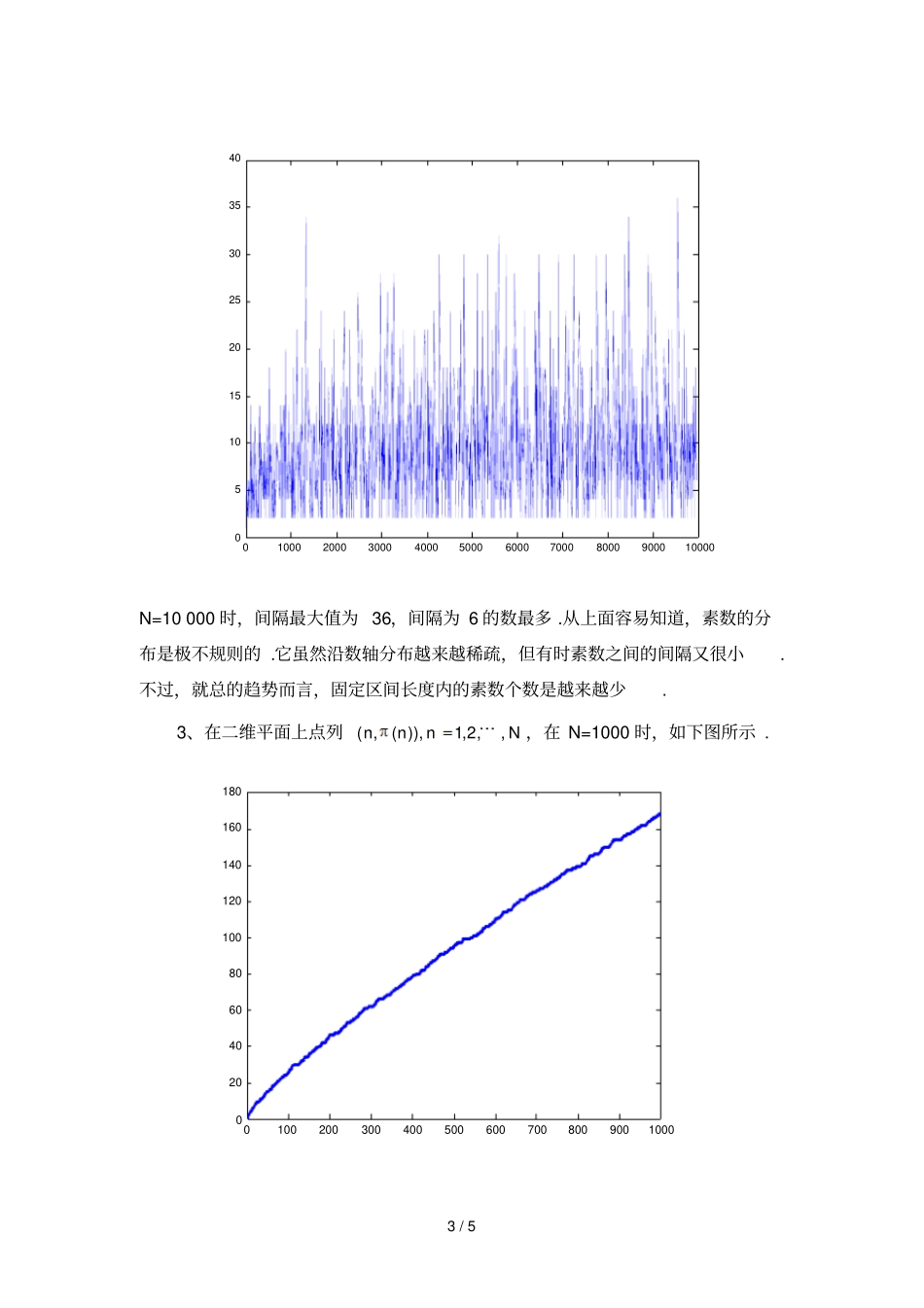
1/5数学实验作业(一)素数的分布一、实验目的观察素数在实轴上的分布,考查素数在实轴上的分布规律,寻找区间上素数个数的近似表达式.二、实验原理及步骤1、用)(n代表不超过n的素数的个数,),(nm表示区间],[nm内素数的个数.试计算),100(),1000(),1000(),10000(),100000(以及)200,100(,)1100,1000(,)10100,10000(,)100100,100000(.从计算结果看,随着整数范围的扩大,素数是越来越稀疏,还是越来越密?考虑一些更长的区间,再尝试以上同样的实验.2、将素数从小到大顺序排列,3,221pp,用nnnppd1表示相邻素数之间的间隔.计算)10000,1000(,,,321NddddN,然后将点),(nndp标在坐标系中,试从中找出素数间隔的规律.比如素数的间隔值有哪些?它们各重复多少次,哪些间隔值重复的次数多,最大间隔是多少?随着N增大,最大间隔值是否也随之增大?3、根据上述实验,对素数的分布做一个猜测,比如间隔为2的素数是否有无穷多个?更一般的,间隔为某个素数是否有无穷多个?是否存在相邻的素数,其间隔值可以无穷大?证明这些猜测.4、在二维平面上标出点列))(,(nn,Nn,,2,1(取不同的N,如1000,10000等).也可以用折线将点连接起来.观察)(n趋于无穷的趋势,并且将它与xyxy,比较.可以得出什么结论?类似的观察点列)/)(,(nnn,)/)(,(nnn及))))ln(//()(,(,(nnnnn.猜测)(n趋于无穷时候的极限.5、令nkknkknRdxxnLi21!)(ln)1(11)(,ln1)(,其中:2/5kkk31211)(.试对一系列充分大的n,计算)08366.1/(ln,ln/),(nnnnn,)(nLi及)(nR.其中哪一个公式更接近)(n?三、实验结果及分析1、通过编制程序计算可以得到,),100(),1000(),10000()100000(的值是:25,168,1229,9592.)200,100(,)1100,1000(,)10100,10000(,)100100,100000(的值分别是:21,16,11,6,从中可以看出,随着整数值的扩大,等间隔范围内的素数是越来越稀疏.2、N=1000时,),(nndp如下图所示.0100200300400500600700800900100002468101214161820N=10000时,),(nndp如下图所示.3/50100020003000400050006000700080009000100000510152025303540N=10000时,间隔最大值为36,间隔为6的数最多.从上面容易知道,素数的分布是极不规则的.它虽然沿数轴分布越来越稀疏,但有时素数之间的间隔又很小.不过,就总的趋势而言,固定区间长度内的素数个数是越来越少.3、在二维平面上点列Nnnn,,2,1)),(,(,在N=1000时,如下图所示.010020030040050060070080090010000204060801001201401601804/5在同一坐标系中作出xyxy,的图有:0100200300400500600700800900100001002003004005006007008009001000绿色线代表y=x,蓝色代表xy,红色线代表))(,(nn.可以看出点列夹在这2条线之间.同样地,作出点列)/)(,(nnn,)/)(,(nnn及))))ln(//()(,(,(nnnnn如下图所示.010020030040050060070080090010000123456黄色的线表示)/)(,(nnn,红色的线表示)/)(,(nnn,从中可以看出)(n在5/5n时的极限的阶在1/2到1之间.4、针对100000,10000,1000,100n,分别计算)08366.1/(ln,ln/),(nnnnn,)(nLi及)(nR.计算结果如下表.)(n)ln(/nn)08366.1/(lnnn)(nLi)(nR1002521.714728.396929.081026.71591000168144.7648171.7005176.5645170.09031000012291085.71230.51245.11229.510000095928685.99588.49628.89590.9从表中容易看出,计算公式)(nR更接近)(n.四、感想及进一步工作通过数学实验和计算机编程,了解到素数在实轴上的分布,即分布式极不规则的,对于固定长度的区间[M,N],其中的素数个数越来越少.素数的个数近似表达式可由)(nR来近似求出.关于素数,还有许许多多富于挑战性的问题,比如Goldback猜想,大整数的素因子分解,完全数,孪生素数,Bertrand猜测,清一色素数等,都等着人们去挑战和解决.