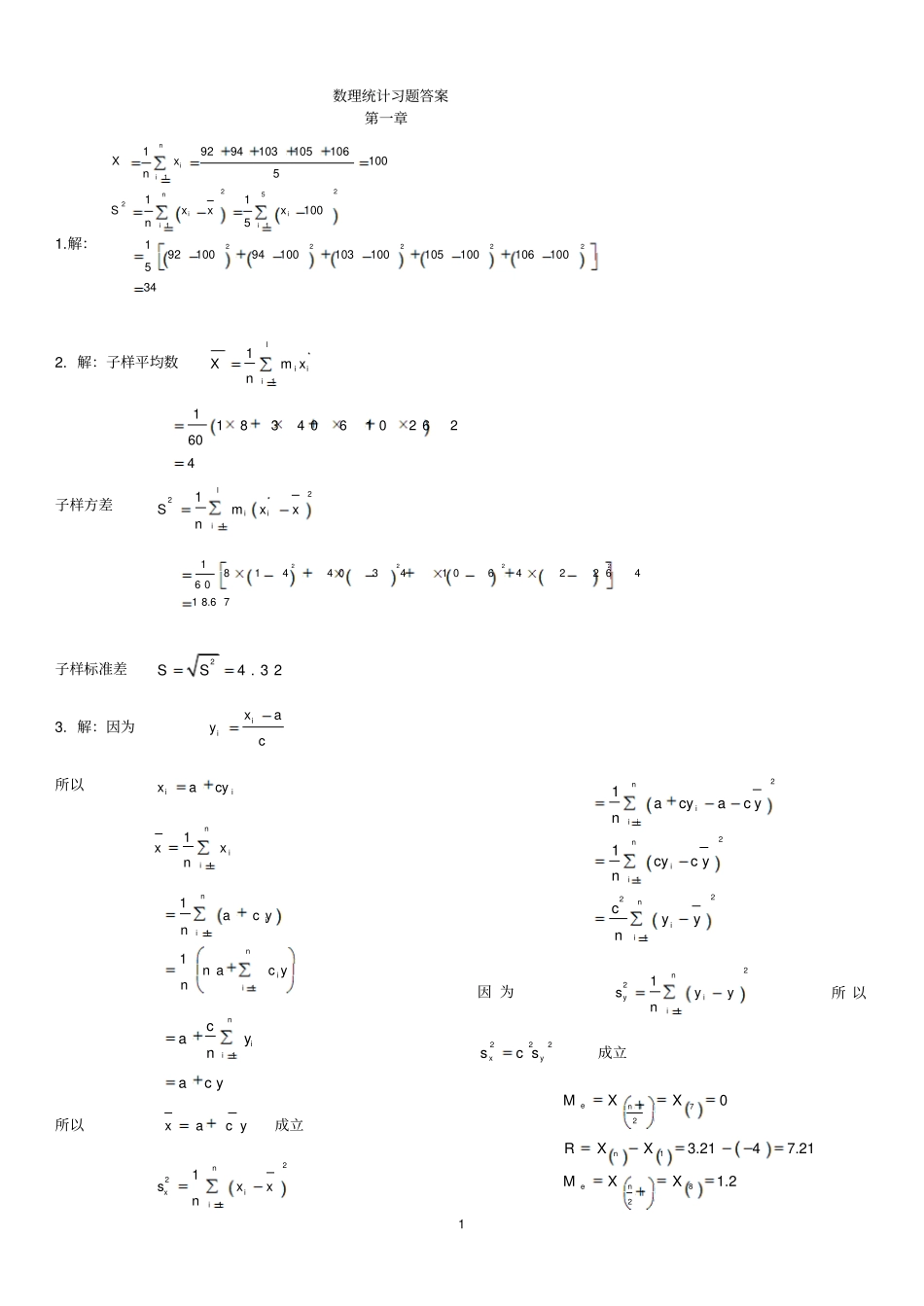1数理统计习题答案第一章1.解:12252112222219294103105106100511100519210094100103100105100106100534niiniiiiXxnSxxxn2.解:子样平均数*11liiiXmxn118340610262604子样方差22*11liiiSmxxn222218144034106422646018.67子样标准差24.32SS3.解:因为iixayc所以iixacy11niixxn1111niiniiacynnacyn1niicaynacy所以xacy成立2211nxiisxxn22122111niiiniiniiacyacyncycyncyyn因为2211nyiisyyn所以222xyscs成立172181203.2147.211.2ennenMXXRXXMXX14.解:变换2000iiyxi123456789ix193916973030242420202909181520202310iy-61-303103042420909-1852031011niiyyn161303103042420909185203109240.4442211nyiisyyn222222222161240.444303240.4441030240.4449424240.44420240.444909240.444185240.44420240.444310240.444197032.247利用3题的结果可知2220002240.444197032.247xyxyss5.解:变换10080iiyxi12345678910111213ix79.9880.0480.0280.0480.0380.0380.0479.9780.0580.0380.0280.0080.02iy-2424334-35320213111113niiiiyyyn12424334353202132.002211nyiisyyn222222122.00322.0052.00342.0013332.0032.005.3077利用3题的结果可知22248080.021005.30771010000yxyxss6.解:变换1027iiyx*ix23.526.128.230.4iy-35-91234im234111liiiymyn13529312434101.52710yx=26.852211lyiiismyyn222212351.5391.54121.5341.510440.252214.4025100xyss7解:身高154158158162162166166170170174174178178182组中值156160164168172176180学生数101426281282*11liiixmxn115610160141642617212168281768180210016622*11liiismxxn2222222110156166141601662616416628168166100121721668176166218016633.4438解:将子样值重新排列(由小到大)-4,-2.1,-2.1,-0.1,-0.1,0,0,1.2,1.2,2.01,2.22,3.2,3.21172181203.2147.211.2ennenMXXRXXMXX9解:121211121211nnijijnxnxnnxnn112212nxnxnn12221121nniisxxnn10.某射手进行20次独立、重复的射手,击中靶子的环数如下表所示:环数10987654频数2309402试写出子样的频数分布,再写出经验分布函数并作出其图形。解:环数10987654频数2309402频率0.10.1500.450.200.120040.1460.3670.75790.9910110xxxFxxxx11.解:区间划分频数频率密度估计值154158100.10.025158162140.140.035162166260.260.065166170280.280.07170174120.120.0317417880.080.0217818220.020.00550100150200身高412.解:ixPiExiDx1,2,,in1122111111nniiiinniiiinEXExExnnnnDXDxDxnnnn13.解:,ixUab2iabEx212ibaDx1,2,,in在此题中1,1ixU0iEx13iDx1,2,,in112111101113nniiiinniiiiEXExExnnDXDxDxnnn14.解:因为2,iXN0iXE1iXD所以0,1iXN1,2,,in由2分布定义可知222111nniiiiXYX服从2分布所以2Yn15.解:因为0,1iXN1,2,,in1230,3XXXN12303XXXE12313XXXD所以1230,13XXXN2212313XXX同理2245613XXX由于2分布的可加性,故522212345612333XXXXXXY可知13C16.解:(1)因为20,iXN1,2,,in0,1iXN所以22121niiXYn11122YYyFyPYyP220yfxdx211'221YYyfyFyf因为2122202200nxnxexnfxx所以21122202200nynnYyeynfyy(2)因为20,iXN1,2,,in0,1iXN所以22221niiXnYn22222220nyYnYnyFyPYyPfxdx6222'22YYnynfyFyf故221222202200nnnynnYnyeynfyy(3)因为20,iXN1,2,,in10,1niiXNn所以22311niiXYnn22333210ynYYFyPYyPyfxdxn233'2211YYyfyFyfnn22110200xexfxxx故23210200ynYeyfynyy(4)因为20,iXN1,2,,in所以1224210,11niiniiXNnXYn224224442210'2211yYYYyFyPYyPfxdxyfyFyf7故24210200yYeyfyyy17.解:因为Xtn存在相互独立的U,V0,1UN2Vn使UXVn221U则221UXVn由定义可知21,Fn18解:因为20,iXN1,2,,in10,1niiXNn221nmiinXm所以1112211nniiiinmnmiiininXmXnYtmXnXm(2)因为0,1iXN1,2,,inm221221niinmiinXnXm8所以221122211,niniiinmnmiiininXmXnYFnmXnXm19.解:用公式计算20.010.019090290U查表得0.012.33U代入上式计算可得20.01909031.26121.2620.解:因为2Xn2En22Dn由2分布的性质3可知0,12XnNn22XncnPXcPnn22212222limcnntnXncncnPedtnnnn故2cnPXcn第二章1.0000,0()0,0()()1()111xxxxxexfxxExfxxdxxedxxeedxex令9从而有1x2.111...