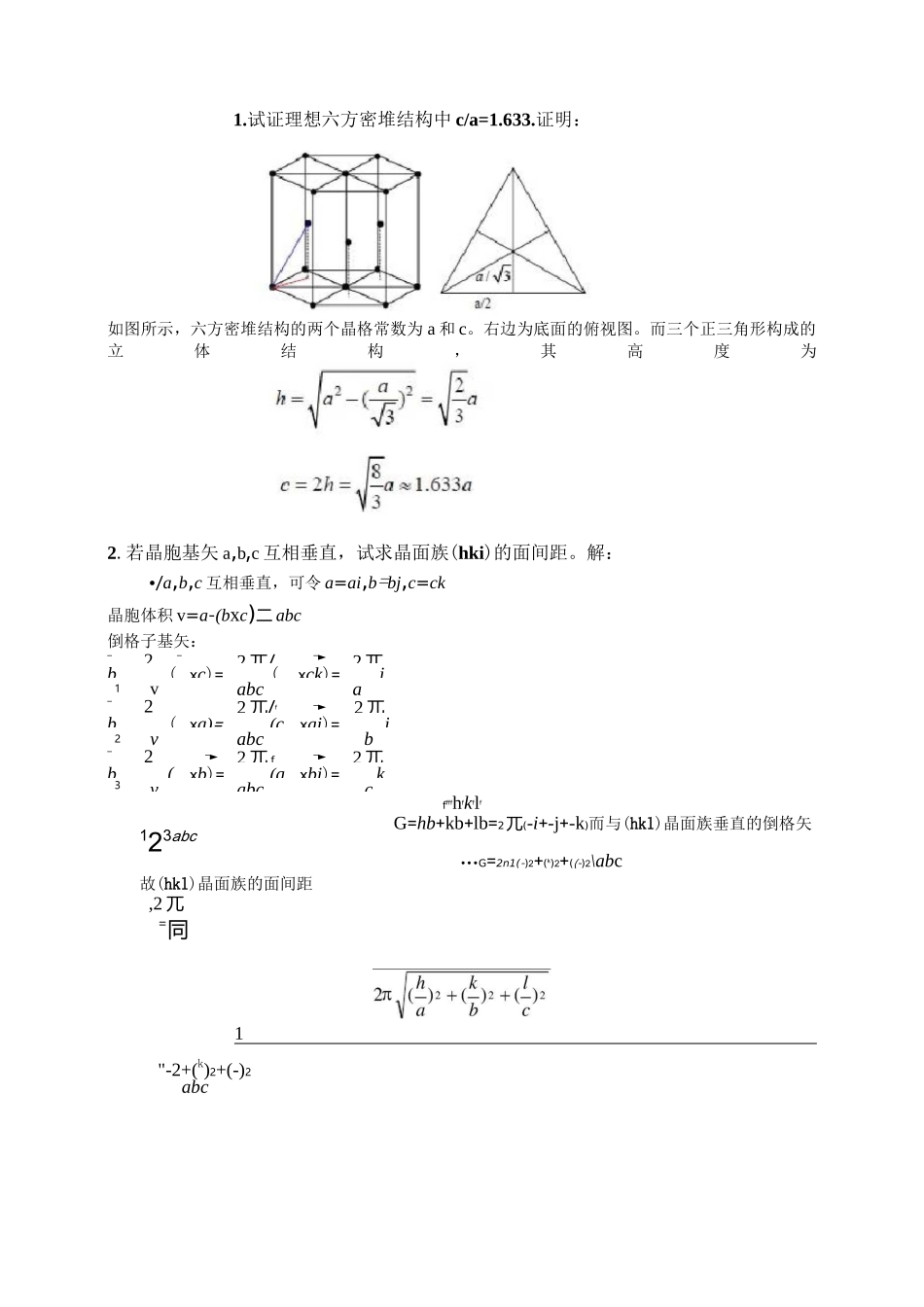
1.试证理想六方密堆结构中c/a=1.633.证明:如图所示,六方密堆结构的两个晶格常数为a和c。右边为底面的俯视图。而三个正三角形构成的立体结构,其高度为2.若晶胞基矢a,b,c互相垂直,试求晶面族(hki)的面间距。解:•/a,b,c互相垂直,可令a=ai,b=bj,c=ck晶胞体积v=a-(bxc)二abc倒格子基矢:―2―2兀/―►2兀b(xc)=(xck)=i1vabca―►22兀/f―►2兀b(xa)=(cxai)=j2vabcb―►2―►2兀f―►2兀b(xb)=(axbj)=k3vabccffffhfkflfG=hb+kb+lb=2兀(-i+-j+-k)而与(hkl)晶面族垂直的倒格矢123abc•••G=2n1(-)2+(k)2+((-)2\abc故(hkl)晶面族的面间距,2兀=同1"-2+(k)2+(-)2abc(111)面面积2J2a(:(p2a)2-('?a)22)_空a•空a_辽a22v22所以原子面密度-(112_4733a2a22110)面11平均每个(110)面有4x^+2x^_2个原子。42(110)面面积a•「2a_、:2a22迈所以(110)面原子面密度G__-5.设二维矩形格子的基矢解:倒格子基矢:a_ai,a_2aj,试画出第一、二、三、布里渊区。12还(axa)_v232aix_兰i(a_xk)a•2a•xa32兀2K—-、2兀-2兀-12兀匚1厂匚_——(axa)_axj_——j_j_—bjv31a•2a•x2a2a21所以倒格子也是二维矩形格子。b方向短一半。--2最近邻b,-b;—-2--次近邻b,-b,2b,-2b;1122—►—►—►—►—►—►—►—►再次近邻b-b,b+b,b-b,-b-b;1-21-22121再再次近邻3b,-3b;22做所有这些点与原点间连线的垂直平分线,围成布里渊区。再按各布里渊区的判断原则进行判断,得:第一布里渊区是一个扁长方形;第二布里渊区是2块梯形和2块三角形组成;第三布里渊区是2对对角三角和4个小三角以及2个等腰梯形组成。3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子?答:通过分析我们知道,原胞可选为简单立方,每个原胞中含有5个原子。体心,八个顶点中取一个,对面面心各取一个原子(即三个)作为基元。布拉菲晶格是简单立方格子。4.试求面心立方结构的(111)和(110)面的原子面密度。解:(111)面11平均每个(111)面有3x+3x=2个原子。626.六方密堆结构的原胞基矢为:-1-<3-a=ai+ai122-1-<3-a=一一ai+a]2223试求倒格子基矢并画出第一布里渊区。解:原胞为简单六方结构。原胞体积:v=a-(axa)123=2a(i+「3j)-£a(-i+j)xck]=2a(i+V3j)-[2ac(j+活)]=4a2c(f3j)-用+j)倒格子基矢:2兀2兀1〜〜2兀〜—-»=(axa)=[—a(-i+「3j)xck]=(i+「3j)v23<323aa2c22兀——2兀—1——2兀——=(axa)=[ckxa(i+耳3j)]=(-i+3j)v31叮32aa2c2b=还(axa)=还k3v12c由此看到,倒格子同原胞一样,只是长度不同,因此倒格子仍是简单六方结构。(注意:倒格子是简单六方,而不是六方密堆)选六边形面心处格点为原点,则最近邻为六个角顶点,各自倒格矢的垂直平分面构成一个六面柱体。次近邻为上下底面中心,其垂直平分面为上下平行平面。再次近邻是上下面六个顶角,其垂直平分面不截上面由最近邻和次近邻垂直平分面构成的六角柱体。所以第一布里渊区是一个六角柱体。比倒格子六方要小。7.略j其中土—=2-aj异号为+;解:设最近邻离子间距离—rijiu(r)=