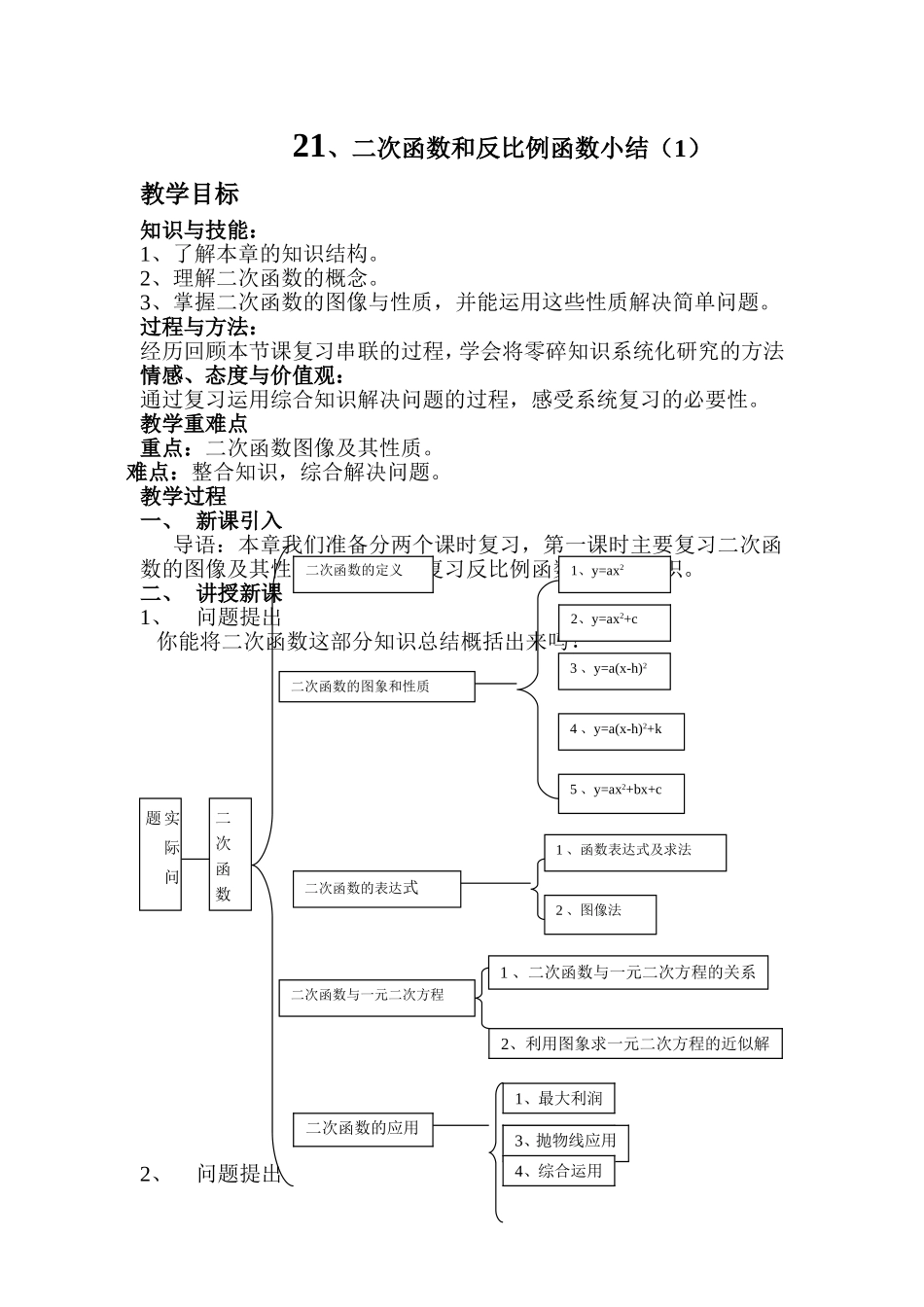
21、二次函数和反比例函数小结(1)教学目标知识与技能:1、了解本章的知识结构。2、理解二次函数的概念。3、掌握二次函数的图像与性质,并能运用这些性质解决简单问题。过程与方法:经历回顾本节课复习串联的过程,学会将零碎知识系统化研究的方法情感、态度与价值观:通过复习运用综合知识解决问题的过程,感受系统复习的必要性。教学重难点重点:二次函数图像及其性质。难点:整合知识,综合解决问题。教学过程一、新课引入导语:本章我们准备分两个课时复习,第一课时主要复习二次函数的图像及其性质,第二课时复习反比例函数的相关知识。二、讲授新课1、问题提出你能将二次函数这部分知识总结概括出来吗?2、问题提出实际问题二次函数二次函数的表达式二次函数与一元二次方程3、y=a(x-h)24、y=a(x-h)2+k5、y=ax2+bx+c1、函数表达式及求法2、图像法二次函数的图象和性质1、二次函数与一元二次方程的关系二次函数的定义1、y=ax22、y=ax2+c二次函数的应用2、利用图象求一元二次方程的近似解1、最大利润2、最大面积3、抛物线应用4、综合运用对照知识结构框图,联系这节的知识体系,你能将这部分知识逐个说出来吗?师生共同归纳二次函数的性质,完成下表函数解析式函数的图象函数具体性质平移规律y=ax2y=ax2+cy=a(x-h)2y=a(x-h)2+ky=ax2+bx+c3、配方法,确定抛物线的开口方向、对称轴和顶点坐标及最值。4、待定系数法求二次函数关系式:(1)一般式:y=ax2+bx+c(a≠0),给出三点坐标,可利用此式来求。(2)顶点式:y=a(x-h)2+k(a≠0),给出二点,且其中一点为顶点时,可利用此式来求。(3)交点式:y=a(x-x1)(x-x2)(a≠0),给出三点,其中两点为与x轴的二个交点(x1,0),(x2,0)时,可利用此式来求。5、二次函数与一元二次方程的关系抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况确定。6二次函数的应用基本思路是:理解问题;分析问题中的变量和常量以及它们之间的关系;用数△>0一元二次方程ax2+bx+c=0有二个不相等的实数根抛物线y=ax2+bx+c与x轴有两个交点△=0抛物线y=ax2+bx+c与x轴有唯一的交点△=0一元二次方程ax2+bx+c=0有二个相等的实数根一元二次方程ax2+bx+c=0有二个相等的实数根抛物线y=ax2+bx+c与x轴有唯一的交点△<0一元二次方程ax2+bx+c=0没有实数根抛物线y=ax2+bx+c与x轴无交点学的方式表示它们之间的关系;列函数求解;检验结果的合理性,拓展等。注意:在学习二次函数要注意数形结合的思想方法。二次函数的图像平移变化,用待定系数法求二次函数的关系式,利用二次函数的图像求解方程和方程组,都体现了数形结合的思想。三、例题分析例1:二次函数y=x2+4x+3的图象可以由二次函数y=x的图象平移而得到,下列平移正确的是()A.先向左平移2个单位,再向上平移1个单位。B.先向左平移2个单位,再向下平移1个单位。C.先向右平移2个单位,再向上平移1个单位。D.先向右平移2个单位,再向下平移1个单位。例2:已知抛物线y=ax2+bx+c经过(-1,0),(0,-3),(2,-3)三点。(1)求这条抛物线的解析式;(2)写出抛物线的开口方向、对称轴和顶点坐标。例3:二次函数y=x2-2(m+1)x+4m的图象与x轴--------()A没有交点B.只有一个交点C.只有二个交点D.至少有一个交点例4已知抛物线y=ax2+x+c与x轴交点的横坐标为-1,则a+c=例5已知二次函数y=x2+bx-1的图象经过点(3,2)。(1)求这个二次函数的关系式。(2)画出它的图象,并指出图象的顶点坐标。(3)当x>0时,求使y≥2的x的取值范围。四、知识巩固P51--53书本复习题A第1、2、3、7、8、10、11、12题;复习题B组第1、2、3、4题。五、小结六、本课主要复习那些知识?通过复习你有那些成功体验?请与同伴交流所得。七、作业布置P51--52复习题A组第4、5、6、9题。