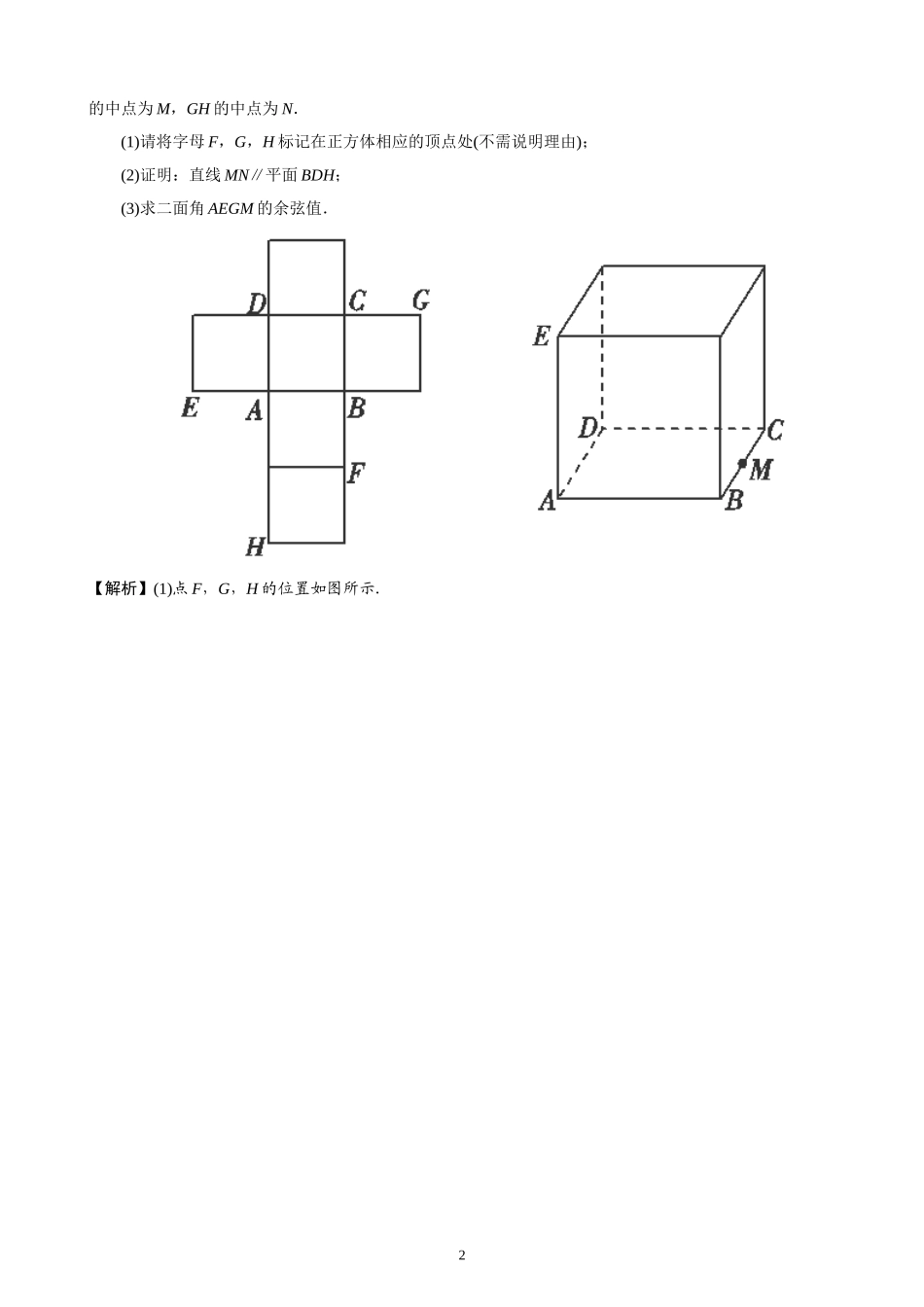
课题立体几何中的折叠、最值、取值范围问题——综合能力提升篇立体几何章节在历来的高考中分值占比重,以两小一大的形式出现较多.空间想象能力是对空间形式的观察、分析、抽象的能力.要在立体几何学习中形成.纵观近几年全国及各省高考试题,对立体几何中的折叠问题、最值问题和探索性问题的考查逐年加重,要求学生要有较强的空间想象力和准确的计算运算能力,才能顺利解答.从实际教学和考试来看,学生对这类题看到就头疼.分析原因,首先是学生的空间想象力较弱,其次是学生对这类问题没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.本文就高中阶段学习和考试出现这类问题加以总结的探讨.题型一:立体几何中的折叠问题折叠与展开问题是立体几何的两个重要问题,这两种方式的转变正是空间几何与平面几何问题转化的集中体现.处理这类题型的关键是抓住两图的特征关系.并弄清折叠前后哪些发生了变化,哪些没有发生变化.这些未变化的已知条件都是我们分析问题和解决问题的依据.而表面展开问题是折叠问题的逆向思维、逆过程,一般地,涉及到多面体表面的问题,解题时不妨将它展开成平面图形试一试.1.如图1,在等腰梯形CDEF中,DE=CD=,EF=2+,将它沿着两条高AD,CB折叠成如图2所示的四棱锥E-ABCD(E,F重合).(1)求证:BE⊥DE;(2)设点M为线段AB的中点,试在线段CE上确定一点N,使得MN∥平面DAE.【解析】(1)证明: AD⊥EF,∴AD⊥AE,AD⊥AB.又 AB∩AE=A,∴AD⊥平面ABE,∴AD⊥BE.由图1和题中所给条件知,AE=BE=1,AB=CD=,∴AE2+BE2=AB2,即AE⊥BE.又 AE∩AD=A,∴BE⊥平面ADE,∴BE⊥DE.(2)取EC的中点G,BE的中点P,连接PM,PG,MG.则MP∥AE,GP∥CB∥DA,∴MP∥平面DAE,GP∥平面DAE. MP∩GP=P,∴平面MPG∥平面DAE. MG⊂平面MPG,∴MG∥平面DAE,即存在点N与G重合满足条件.2.(2015·四川卷)一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设BC1的中点为M,GH的中点为N.(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);(2)证明:直线MN∥平面BDH;(3)求二面角AEGM的余弦值.【解析】(1)点F,G,H的位置如图所示.2(2)证明:连接AC,BD交于点O,连接OH,OM.因为M,N分别是BC,GH的中点,所以OM∥CD,且OM=CD,HN∥CD,且HN=CD,所以OM∥HN,OM=HN,所以四边形MNHO是平行四边形,从而MN∥OH.又MN⊄平面BDH,OH⊂平面BDH,所以MN∥平面BDH.(3)方法一:过M作MP⊥AC于P.在正方体ABCDEFGH中,AC∥EG,所以MP⊥EG.过P作PK⊥EG于K,连接KM,所以EG⊥平面PKM,从而KM⊥EG,所以∠PKM是二面角AEGM的平面角.设AD=2,则CM=1,PK=2.在Rt△CMP中,PM=CMsin45°=.在Rt△PKM中,KM==.所以cos∠PKM==,即二面角AEGM的余弦值为.方法二:如图,以D为坐标原点,分别以DA,DC,DH方向为x轴,y轴,z轴的正方向,建立空间直角坐标系D-xyz.设AD=2,则M(1,2,0),G(0,2,2),E(2,0,2),O(1,1,0),所以GE=(2,-2,0),MG=(-1,0,2).[来源:学科网]设平面EGM的一个法向量为n1=(x,y,z),由得取x=2,得n1=(2,2,1).在正方体ABCDEFGH中,DO⊥平面AEGC,则可取平面AEG的一个法向量为n2=DO=(1,1,0),所以cos〈n1,n2〉===,故二面角AEGM的余弦值为.题型二、立体几何中的最值问题结合近年来全国各省市的高考中,考查与空间图形有关的线段、角、距离、面积、体积等最值问题常常在高考试题中出现.在解决此类问题时,通常应注意分析题目中所有的条件,首先应该在充分理解题意的基础上,分析是否能用公理与定义直接解决题中问题;如果不能,再看是否可将问题条件转化为函数,若能写出确定的表意函数,则可用建立函数法求解;再不能,则要考虑其中是否存在不等关系,看是否能运用解等不式法求解;还不行则应考虑是否可将其体图展开成平面,这样依次顺序思考,基本可以找到解题的途径.33.如图所示,三棱柱ABC-A1B1C1的侧棱长为3,底面边长A1C1=B1C1=1,且∠A1C1B1=90°,D点在棱AA1上且AD=2DA1,P点在棱C1C上,则PD·PB1的最小值为()A.B.-C.D.-【解析】建...