函数的基本性质单调性VIP免费

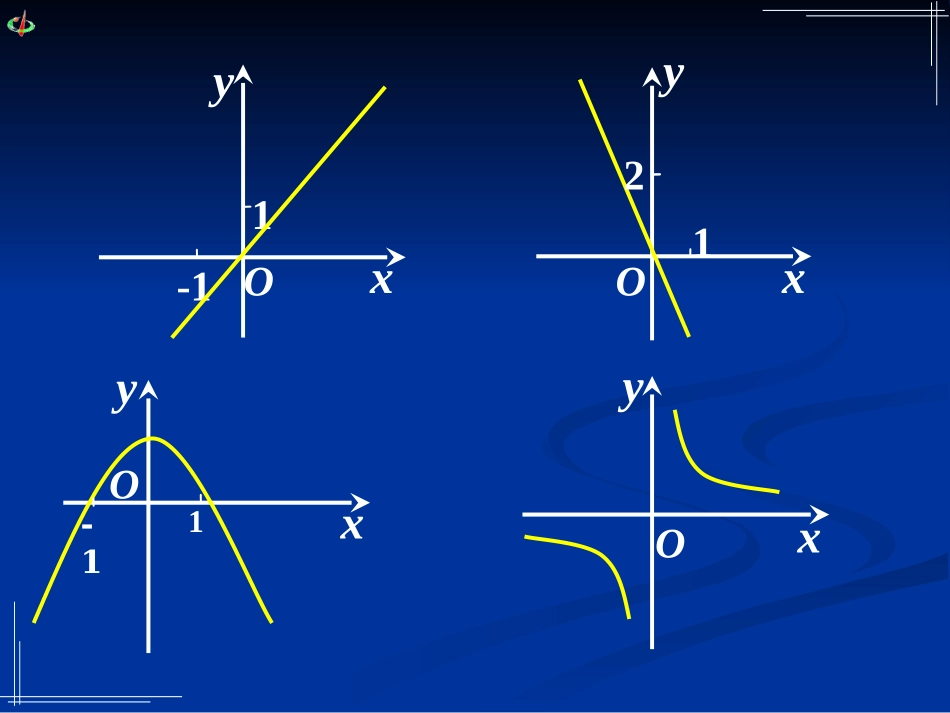
问题1：函数是描述事物运动变化规律的数学模型，如果了解了函数的变化规律，那么也就基本把握了相应事物的变化规律。在事物变化过程中，保持不变的特征就是这个事物的性质。观察下面各个函数图像，你能说说它们分别反映了相应函数的那些变化规律吗？xy21yxO1-11OOOyyxx-11.3函数的基本性质——单调性xyxyxyyxyxyxy研究一次函数和二次函数图像随增大，值变化情况。xxf)(2)(xxfxyxy2xyO二次函数，列出的对应值表2)(xxfyx,-4-4-3-3-2-2-1-100112233441616994411001144991616x2)(xxf2)(xxf-4-4-3-3-2-2-1-100112233441616994411001144991616x1x)(1xfxy2xyO1x)(1xfxy2xyO01x)(1xfxy2xyO1x)(1xfxy2xyO1x)(1xfxy2xyO1x)(1xfxy2xyO1x)(1xfxy2xyO1x)(1xfxy2xyO1x)(1xfxy2xyOx从对应值表及函数图像可以发现：在区间上，随着的增大，相应的反而随着减少；在区间上，随着的增大，相应的也随着增大。)(xfx,00,)(xf形象描述为：设函数的定义域为I.区间在区间D上,若函数图像（从左至右看）总是上升，则称函数在区间D上是增函数.在区间D上,若函数图像（从左至右看）总是下降的，则称函数在区间D上是减函数ID如何用x与f(x)来描述上升的图象？Oxy如何用x与f(x)来描述上升的图象？Oxy如何用x与f(x)来描述上升的图象？Oxy如何用x与f(x)来描述上升的图象？x2x1Oxyx1＜x2如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)x1＜x2如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)x1＜x2如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)x1＜x2如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)x1＜x2f(x1)f(x2)如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)x1＜x2f(x1)＜f(x2)如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)在给定区间上任取x1,x2x1＜x2f(x1)＜f(x2)如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)在给定区间上任取x1,x2x1＜x2f(x1)＜f(x2)如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)在给定区间上任取x1,x2函数f(x)在给定区间上为增函数.x1＜x2f(x1)＜f(x2)如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)在给定区间上任取x1,x2如何用x与f(x)来描述下降的图象？x2x1Oxyy＝f(x)f(x1)f(x2)函数f(x)在给定区间上为增函数.x1＜x2f(x1)＜f(x2)如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)在给定区间上任取x1,x2如何用x与f(x)来描述下降的图象？x2x1Oxyy＝f(x)f(x1)f(x2)函数f(x)在给定区间上为增函数.在给定区间上任取x1,x2x1＜x2f(x1)＜f(x2)如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)在给定区间上任取x1,x2如何用x与f(x)来描述下降的图象？x2x1Oxyy＝f(x)f(x1)f(x2)函数f(x)在给定区间上为增函数.x1＜x2f(x1)＞f(x2)在给定区间上任取x1,x2x1＜x2f(x1)＜f(x2)如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)在给定区间上任取x1,x2如何用x与f(x)来描述下降的图象？x2x1Oxyy＝f(x)f(x1)f(x2)函数f(x)在给定区间上为增函数.函数f(x)在给定区间上为减函数.x1＜x2f(x1)＞f(x2)在给定区间上任取x1,x2增函数、减函数的概念：增函数、减函数的概念：一般地，设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2，当x1＜x2时，都有f(x1)＜f(x2)，那么就说f(x)在这个区间D上是增函数.增函数、减函数的概念：一般地，设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2，当x1＜x2时，都有f(x1)＜f(x2)，那么就说f(x)在这个区间D上是增函数.2.如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2，当x1＜x2时，都有f(x1)＞f(x2)，那么就说f(x)在这个区间D上是减函数.增函数、减函数的概念：一般地，设函数f(x)的定义域为I.1.如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2，当x1＜x2时，都有f(x1)＜f(x2)，那么就说f(x)在这个区间D上是增函数.2...