高中数学 双基限时练2 新人教A版必修4-新人教A版高一必修4数学试题VIP免费

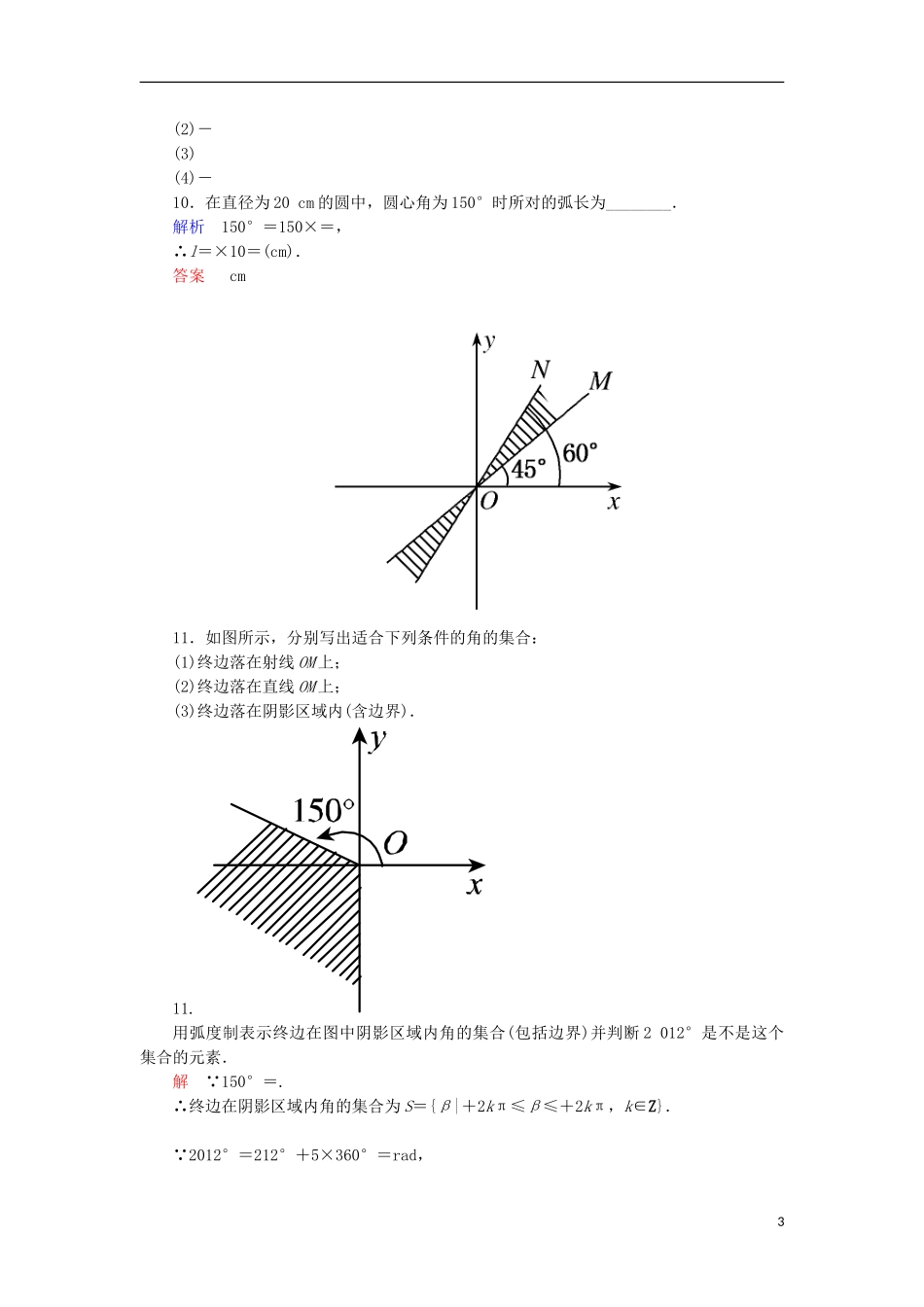
双基限时练(二)1．终边在y轴的非负半轴上的角的集合是()A．{α|α＝kπ，k∈Z}B.C．{α|α＝2kπ，k∈Z}D.解析A选项表示的角的终边在x轴上；B选项表示的角的终边在y轴上；C选项表示的角的终边在x轴非负半轴上；D选项表示的角的终边在y轴非负半轴上，故选D.答案D2．在半径为5cm的圆中，圆心角为周角的的角所对的圆弧长为()A.cmB.cmC.cmD.cm解析记r＝5，圆心角α＝×2π＝，∴l＝|α|r＝π.答案B3．将－1485°化成α＋2kπ(0≤α<2π，k∈Z)的形式是()A．－－8πB.π－8πC.－10πD.－10π解析∵－1485°＝－5×360°＋315°，又2π＝360°，315°＝π，∴－1485°＝－5×2π＋π＝－10π.答案D4．把－π表示成θ＋2kπ(k∈Z)的形式，使|θ|最小的θ为()A．－πB.C.πD．－解析∵－＝－2π－，∴θ＝－π.又－＝－4π＋，∴θ＝.∴使|θ|最小的θ＝－.答案A5．若一圆弧长等于其所在圆的内接正三角形的边长，则其圆心角的弧度数的绝对值为()A.B.C.D．2解析设所在圆的半径为r，圆内接正三角形的边长为2rsin60°＝r，所以弧长r的圆心角的弧度数为＝.答案C16．用集合表示终边在阴影部分的角α的集合为()A.B.C.D.解析由图可知在[0,2π)内角的终边落在阴影部分时≤α≤，∴满足条件的集合为.答案D7．圆的半径变为原来的，而弧长不变，则该弧所对的圆心角变为原来的________倍．解析由公式θ＝知，半径r变为原来的，而弧长不变，则该弧所对的圆心角变为原来的2倍．答案28．将下列弧度转化为角度：(1)＝________；(2)－＝________；(3)＝________；(4)－π＝________.答案(1)15°(2)－157°30′(3)390°(4)－75°9．将下列角度化为弧度：(1)36°＝________rad；(2)－105°＝________rad；(3)37°30′＝________rad；(4)－75°＝________rad.解析利用1°＝rad计算．答案(1)2(2)－(3)(4)－10．在直径为20cm的圆中，圆心角为150°时所对的弧长为________．解析150°＝150×＝，∴l＝×10＝(cm)．答案cm11．如图所示，分别写出适合下列条件的角的集合：(1)终边落在射线OM上；(2)终边落在直线OM上；(3)终边落在阴影区域内(含边界)．11.用弧度制表示终边在图中阴影区域内角的集合(包括边界)并判断2012°是不是这个集合的元素．解∵150°＝.∴终边在阴影区域内角的集合为S＝{β|＋2kπ≤β≤＋2kπ，k∈Z}．∵2012°＝212°＋5×360°＝rad，3又＜＜.∴2012°＝∈S.12.如图所示，动点P、Q从点A(4,0)出发沿圆周运动，点P按逆时针方向每秒钟转弧度，点Q按顺时针方向每秒钟转弧度，求P、Q第一次相遇所用的时间及P、Q各自走过的弧长．解设P、Q第一次相遇时所用的时间为t秒，则：t·＋t·＝2π，解得t＝4，即第一次相遇时所用的时间为4秒．P点走过的弧长为：π×4＝π，Q点走过的弧长为：8π－＝.13．扇形AOB的周长为8cm.(1)若这个扇形的面积为3cm2，求圆心角的大小；(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB.解(1)设扇形的圆心角为θ，扇形所在圆的半径为R，依题意有解得θ＝或6.即圆心角的大小为弧度或6弧度．(2)设扇形所在圆的半径为xcm，则扇形的圆心角θ＝，于是扇形的面积是S＝x2·＝4x－x2＝－(x－2)2＋4.故当x＝2cm时，S取到最大值．此时圆心角θ＝＝2弧度，弦长AB＝2·2sin1＝4sin1(cm)．即扇形的面积取得最大值时圆心角等于2弧度，弦长AB等于4sin1cm.4