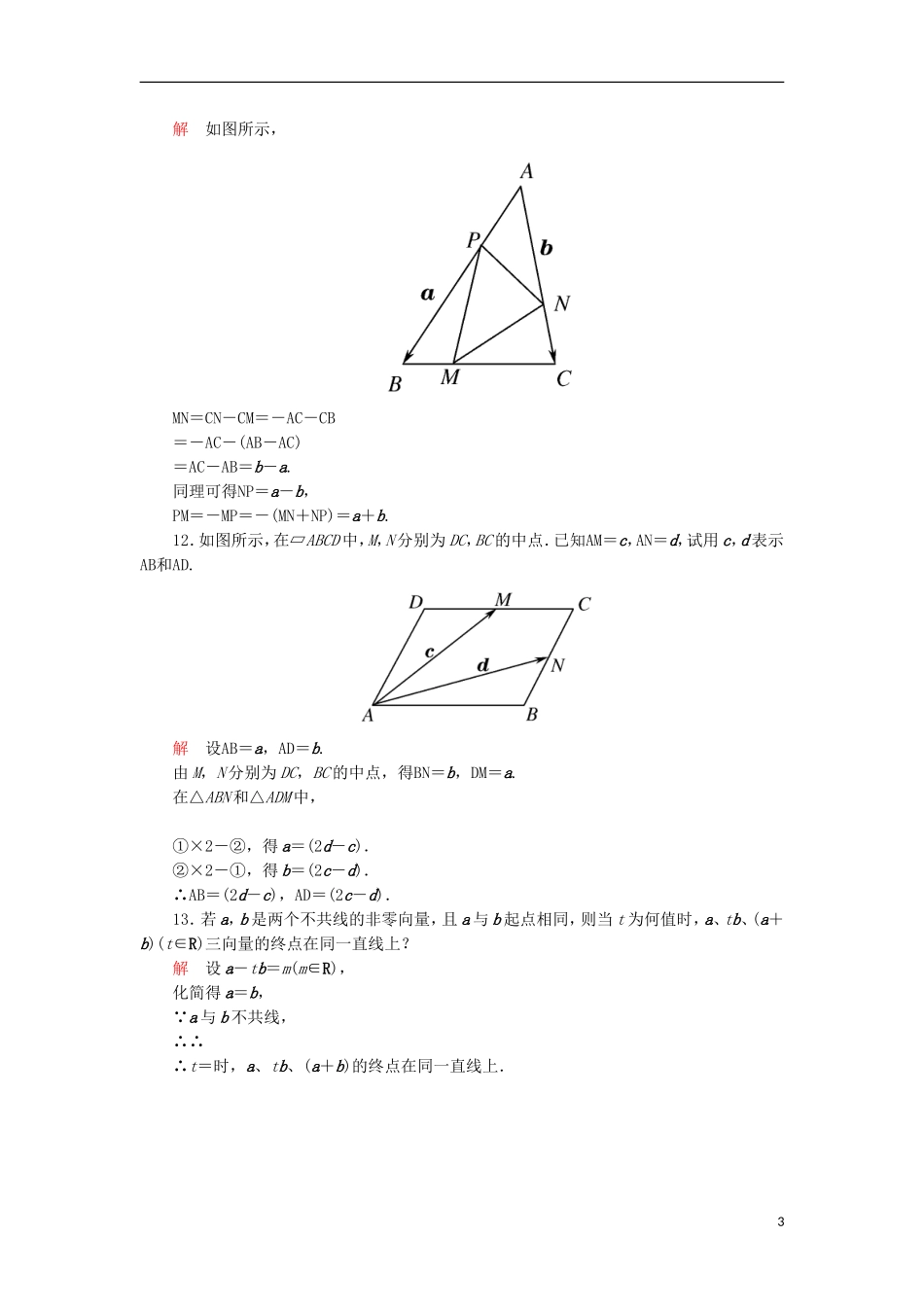
双基限时练(十七)1.给出下面三种说法:①一个平面内只有一对不共线的非零向量可作为表示该平面所有向量的基底;②一个平面内有无数多对不共线的非零向量可作为表示该平面所有向量的基底;③零向量不可为基底中的向量.其中正确的说法是()A.①②B.②③C.①③D.②解析因为不共线的两个向量都可以作为一组基底,所以一个平面内有无数多个基底,又零向量和任何向量共线,所以基底中不含有零向量.因此本题中,①错,②、③正确,故选B.答案B2.已知e1和e2是表示平面内所有向量的一组基底,那么下面四组向量中不能作为一组基底的是()A.e1和e1+e2B.e1-2e2和e2-2e1C.e1-2e2和4e2-2e1D.e1+e2和e1-e2解析分析四个选项知,在C中,4e2-2e1=-2(e1-2e2).∴e1-2e2与4e2-2e1共线,应选C.答案C3.在△ABC中,BC=3BD,则AD等于()A.(AC+2AB)B.(AB+2AC)C.(AC+3AB)D.(AC+2AB)解析如图所示,AD=AB+BD=AB+BC=AB+(AC-AB)=AB+AC=(AC+2AB),故选A.答案A4.已知四边形ABCD是菱形,点P在对角线AC上(不包括端点A,C),则AP等于()A.λ(AB+AD),λ∈(0,1)B.λ(AB+BC),λ∈C.λ(AB-AD),λ∈(0,1)D.λ(AB-BC),λ∈解析∵ABCD是菱形,且AC是一条对角线,由向量加法的平行四边形法则知,AC=AB+1AD,而点P在AC上,∴三点A,P,C共线,∴AP=λAC=λ(AB+AD),显然λ∈(0,1),故选A.答案A5.平面内有四边形ABCD和点O,若OA+OC=OB+OD,则四边形ABCD的形状是()A.梯形B.平行四边形C.矩形D.菱形解析因为OA+OC=OB+OD,所以OA-OB=OD-OC,即BA=CD.又A,B,C,D四点不共线,所以|BA|=|CD|,且BA∥CD,故四边形ABCD为平行四边形.答案B6.如图所示,点P在∠AOB的对角区域MON的阴影内,满足OP=xOA+yOB,则实数对(x,y)可以是()A.B.C.D.解析由图观察并根据平面向量基本定理,可知x<0,y<0,故选C.答案C7.已知a,b不共线,且c=λ1a+λ2b(λ1,λ2∈R),若c与b共线,则λ1=________.解析∵a,b不共线,∴a,b可以作为一组基底,又c与b共线,∴c=λ2b,∴λ1=0.答案08.设向量a,b不共线,且OC1=k1a+k2b,OC2=h1a+h2b,若OC1+OC2=ma+nb,则实数m=________,n=________.解析OC1+OC2=(k1+h1)a+(k2+h2)b=ma+nb.∴m=k1+h1,n=k2+h2.答案k1+h1k2+h29.已知e1,e2不共线,a=e1+2e2,b=2e1+λe2,要使a,b能作为平面内所有向量的一组基底,则实数λ的取值范围是________.解析使a、b为基底,则使a、b不共线,∴λ-2×2≠0.∴λ≠4.答案{λ|λ≠4}10.若a≠0,且b≠0,且|a|=|b|=|a-b|,则a与a+b的夹角是________.答案30°11.设M,N,P是△ABC三边上的点,它们使BM=BC,CN=CA,AP=AB,若AB=a,AC=b,试用a,b将MN,NP,PM表示出来.2解如图所示,MN=CN-CM=-AC-CB=-AC-(AB-AC)=AC-AB=b-a.同理可得NP=a-b,PM=-MP=-(MN+NP)=a+b.12.如图所示,在▱ABCD中,M,N分别为DC,BC的中点.已知AM=c,AN=d,试用c,d表示AB和AD.解设AB=a,AD=b.由M,N分别为DC,BC的中点,得BN=b,DM=a.在△ABN和△ADM中,①×2-②,得a=(2d-c).②×2-①,得b=(2c-d).∴AB=(2d-c),AD=(2c-d).13.若a,b是两个不共线的非零向量,且a与b起点相同,则当t为何值时,a、tb、(a+b)(t∈R)三向量的终点在同一直线上?解设a-tb=m(m∈R),化简得a=b,∵a与b不共线,∴∴∴t=时,a、tb、(a+b)的终点在同一直线上.3