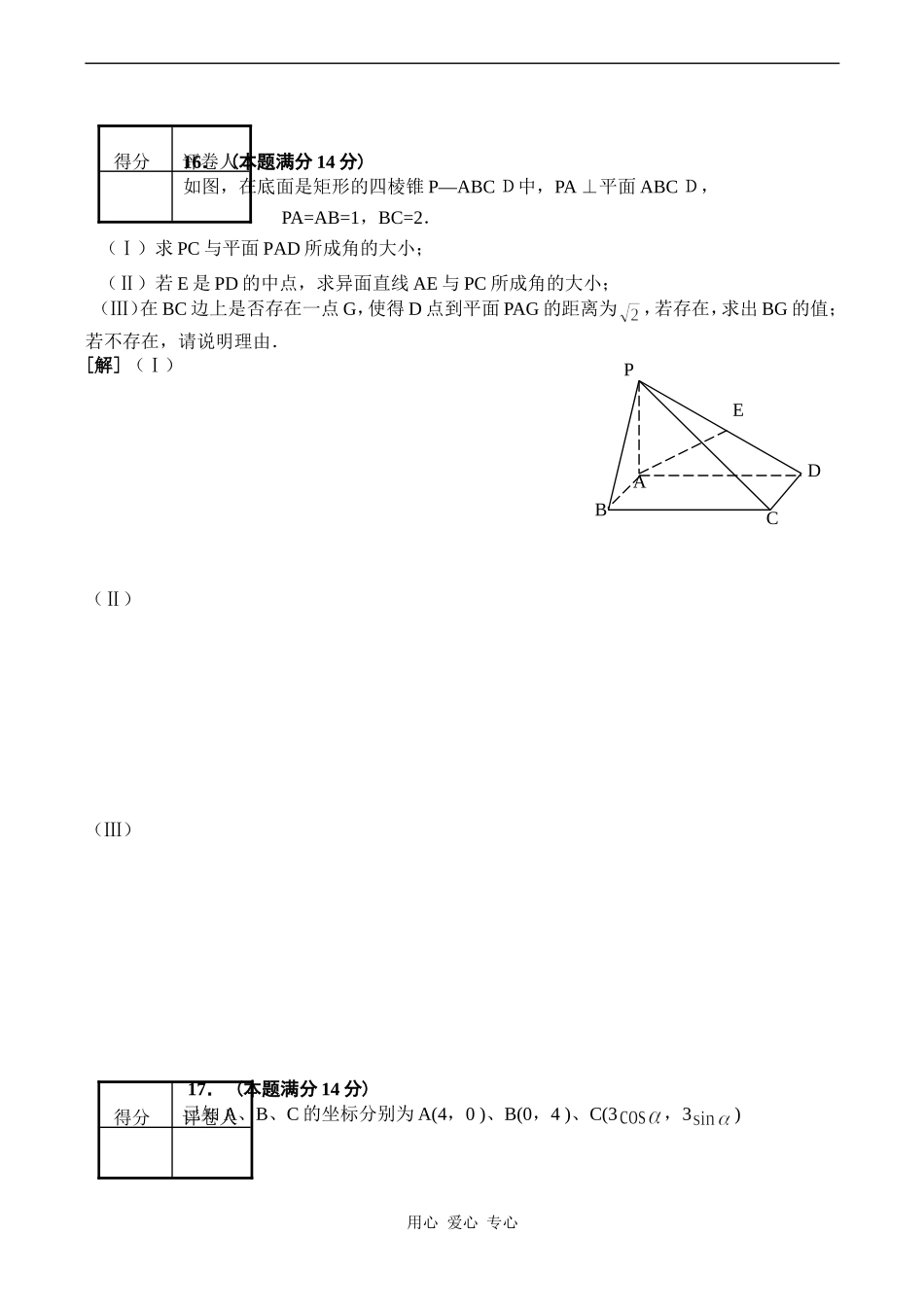
上海市闸北区高考数学二轮模拟测试卷(理)(考试时间:120分钟满分:150分)一.填空题(本大题满分40分)本大题共有10题,只要求直接填写结果,每题填对得4分,否则一律得零分.1.抛物线的焦点坐标为.2.函数的最小正周期为________.3.若,则.4.已知虚数z满足等式:,则.5.椭圆=1上一点P到两焦点的距离之积为m,则m的最大值为.6.如图,正方体的棱长为,将该正方体沿对角面切成两块,再将这两块拼接成一个不是正方体的四棱柱,那么所得四棱柱的全面积为__________.7.某商场开展促销抽奖活动,摇出的中奖号码是8,2,5,3,7,1,参加抽奖的每位顾客从0~9这10个号码中任意抽出六个组成一组,若顾客抽出的六个号码中至少有5个与摇出的号码相同(不计顺序)即可得奖,则中奖的概率是________.8.已知关于的方程组有两组不同的解,则实数的取值范围是____________.9.函数在区间上是增函数的充要条件是_______________.10.请写出方程的一组解为二.选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,不选、选错一律得零分.11.在数列中,,且,则为()A.1B.2C.-1D.-212.已知边长为1的正三角形中,则的值为()用心爱心专心得分评卷人得分评卷人ABCDA1D1B1C1A.B.C.D.13.在极坐标系中,曲线关于()A.直线轴对称B.直线轴对称C.点中心对称D.极点中心对称14.设奇函数的定义域为,最小正周期为,若,则的取值范围是()A.或B.C.D.三.解答题(本大题满分94分)本大题共有6题,解答下列各题必须写出必要的步骤.15.(本题满分12分)设同时满足条件和对任意都有成立.(Ⅰ)求f(x)的解析表达式;(Ⅱ)设函数的定义域为,且在定义域内,.求;(Ⅲ)求函数的值域.[解](Ⅰ)(Ⅱ)(Ⅲ)用心爱心专心得分评卷人16.(本题满分14分)如图,在底面是矩形的四棱锥P—ABCD中,PA⊥平面ABCD,PA=AB=1,BC=2.(Ⅰ)求PC与平面PAD所成角的大小;(Ⅱ)若E是PD的中点,求异面直线AE与PC所成角的大小;(Ⅲ)在BC边上是否存在一点G,使得D点到平面PAG的距离为,若存在,求出BG的值;若不存在,请说明理由.[解](Ⅰ)(Ⅱ)(Ⅲ)17.(本题满分14分)已知A、B、C的坐标分别为A(4,0)、B(0,4)、C(3,3)用心爱心专心得分评卷人得分评卷人PABCDE(Ⅰ)若,且.求角α的值;(Ⅱ)若,求的值.[解](Ⅰ)(Ⅱ)18.(本题满分16分)某农贸公司按每担200元收购某农产品,并按每100元纳税10元(又称征税率为10个百分点),计划可收购a万担.政府为了鼓励收购公司多收购这种农产品,决定征税率降低个百分点,预测收购量可增加2x个百分点.(Ⅰ)写出税收y(万元)与x的函数关系式;(Ⅱ)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围.[解](Ⅰ)(Ⅱ)用心爱心专心得分评卷人19.(本题满分18分)等差数列的前项和为.(Ⅰ)求数列的通项与前项和;(Ⅱ)设,中的部分项恰好组成等比数列,且,求数列的通项公式;(III)设,求证:数列中任意不同的三项都不可能成为等比数列.[解](Ⅰ)(Ⅱ)(III)用心爱心专心得分评卷人20.(本题满分20分)如图,椭圆:,、、、为椭圆的顶点.(Ⅰ)设点,若当且仅当椭圆上的点在椭圆的顶点时,取得最大值与最小值,求的取值范围;(Ⅱ)若椭圆上的点到焦点距离的最大值为,最小值为,且与直线相交于,两点(不是椭圆的左右顶点),并满足.试研究:直线是否过定点?若过定点,请求出定点坐标,若不过定点,请说明理由.[解](Ⅰ)用心爱心专心得分评卷人yB2PA1MOA2xB1(Ⅱ)闸北区08届高三数学(理)学科期中练习卷参考答案与评分标准一.填空题1.;2.;3.2;4.1+2i;5.25;6.;7.;8.;9.;10..二.选择题11.A;12.D;13.B;14.C.三.解答题15.17.解:(1)由,得,………………………………………………….1分由,得由得,………………………………………………………………….2分…………………………………………………………………….1分(2)()……………………………………...