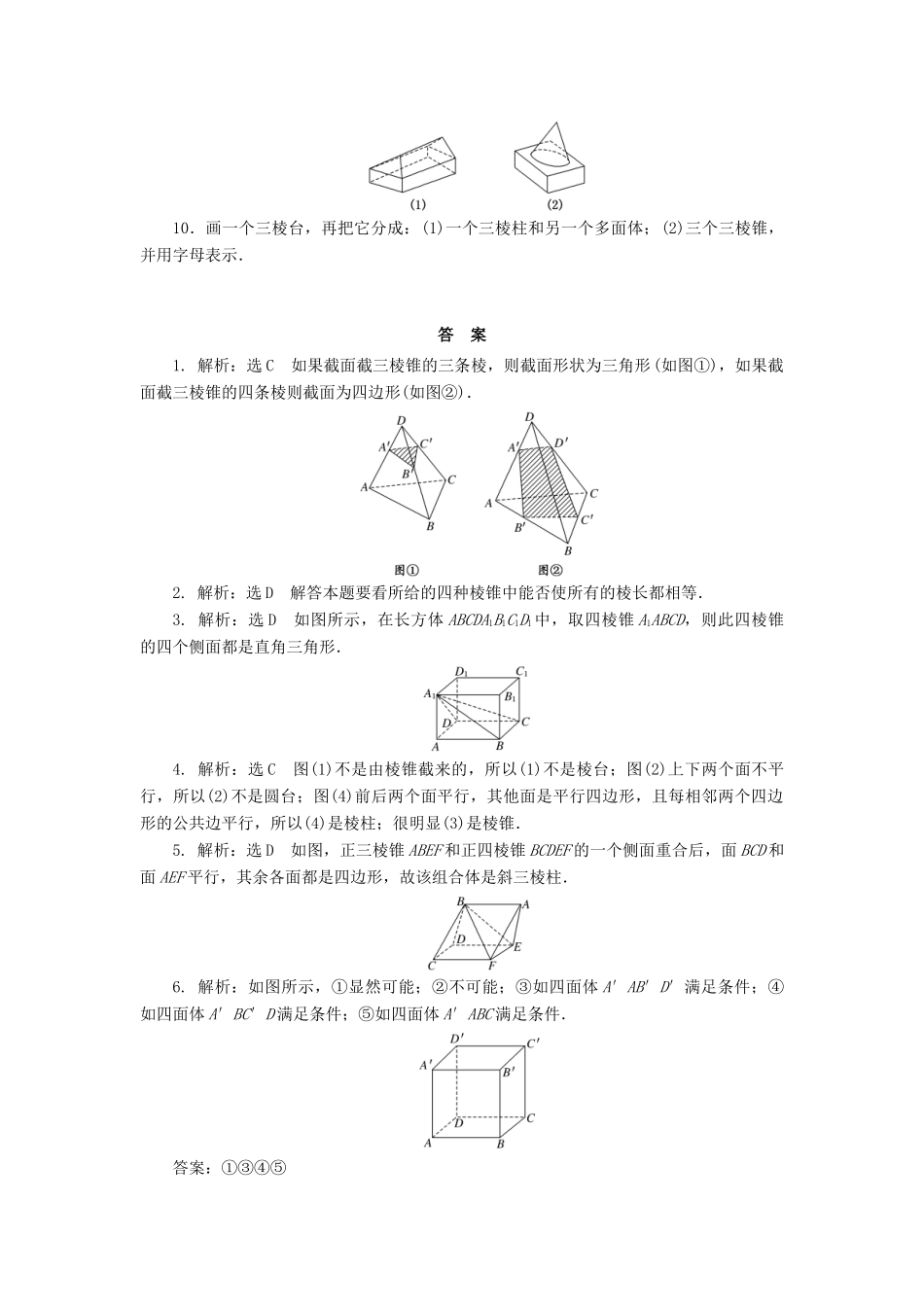
课下能力提升(二)简单多面体一、选择题1.用一个平面去截一个三棱锥,截面形状是()A.四边形B.三角形C.三角形或四边形D.不可能为四边形2.若正棱锥的底面边长和侧棱长相等,则该棱锥一定不是()A.三棱锥B.四棱锥C.五棱锥D.六棱锥3.在四棱锥的四个侧面中,直角三角形最多可有()A.1个B.2个C.3个D.4个4.观察图中四个几何体,其中判断正确的是()A.(1)是棱台B.(2)是圆台C.(3)是棱锥D.(4)不是棱柱5.有一个正三棱锥和一个正四棱锥,它们所有的棱长都相等,把这个正三棱锥的一个侧面重合在正四棱锥的一个侧面上,则所得到的这个组合体是()A.底面为平行四边形的四棱柱B.五棱锥C.无平行平面的六面体D.斜三棱柱二、填空题6.在正方体上任意选择四个顶点,它们可能是如下各种几何形体的四个顶点,这些几何形体是________(写出所有正确结论的编号).①矩形;②不是矩形的平行四边形;③有三个面是等腰直角三角形,有一个面是等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.7.下列四个命题:(1)棱柱的两底面是全等的正多边形;(2)有一个侧面是矩形的棱柱是直棱柱;(3)有两个侧面是矩形的棱柱是直棱柱;(4)四棱柱的四条体对角线两两相等,则该四棱柱为直四棱柱.其中正确的序号是________.8.用铁丝作一个三角形,在三个顶点分别固定一根筷子,把三根筷子的另一端也可用铁丝连成一个三角形,从而获得一个几何模型,如果筷子长度相等,那么这个几何体可能是____________.三、解答题9.指出如图所示图形是由哪些简单几何体构成.10.画一个三棱台,再把它分成:(1)一个三棱柱和另一个多面体;(2)三个三棱锥,并用字母表示.答案1.解析:选C如果截面截三棱锥的三条棱,则截面形状为三角形(如图①),如果截面截三棱锥的四条棱则截面为四边形(如图②).2.解析:选D解答本题要看所给的四种棱锥中能否使所有的棱长都相等.3.解析:选D如图所示,在长方体ABCDA1B1C1D1中,取四棱锥A1ABCD,则此四棱锥的四个侧面都是直角三角形.4.解析:选C图(1)不是由棱锥截来的,所以(1)不是棱台;图(2)上下两个面不平行,所以(2)不是圆台;图(4)前后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以(4)是棱柱;很明显(3)是棱锥.5.解析:选D如图,正三棱锥ABEF和正四棱锥BCDEF的一个侧面重合后,面BCD和面AEF平行,其余各面都是四边形,故该组合体是斜三棱柱.6.解析:如图所示,①显然可能;②不可能;③如四面体A′AB′D′满足条件;④如四面体A′BC′D满足条件;⑤如四面体A′ABC满足条件.答案:①③④⑤7.解析:(1)棱柱的两底面全等,但不一定是正多边形;(2),(3)都不能保证侧棱与底面垂直;(4)易知对角面是长方形,侧棱与底面垂直,正确.答案:(4)8.解析:在该模型中已知一面为三角形,则根据筷子的位置情况,判断即可.答案:三棱柱或三棱台9.解:分割原图,使它们每一部分都是简单几何体.(1)是一个三棱柱和一个四棱柱组成的几何体.(2)是一个圆锥和一个四棱柱组合而成的几何体.10.解:画三棱台一定要利用三棱锥.(1)如图①所示,三棱柱是棱柱A′B′C′AB″C″.(2)如图②所示,三个三棱锥分别是A′ABC,B′A′BC,C′A′B′C.