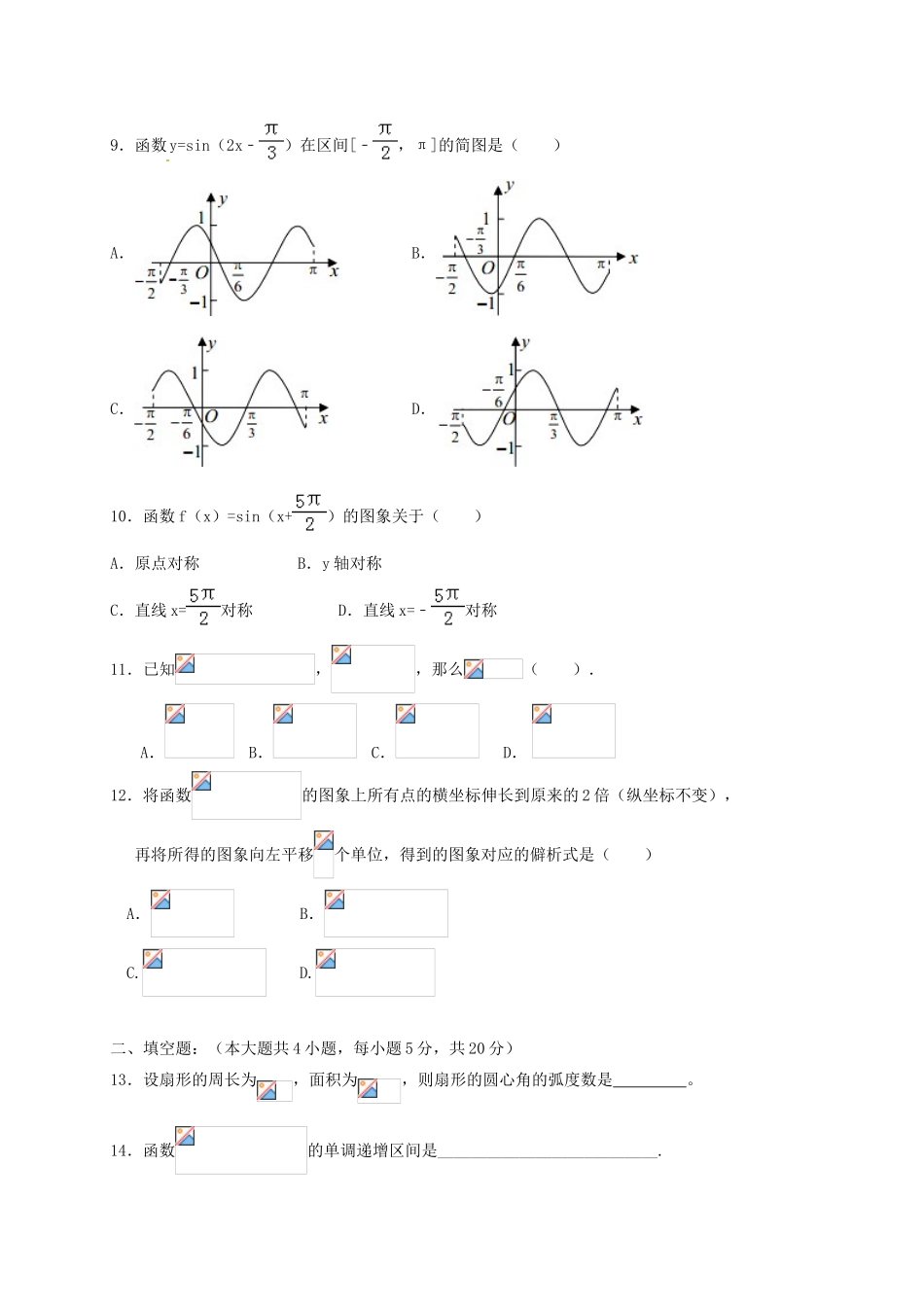
河南省兰考县2016-2017学年高一数学下学期第一次月考试题一、选择题:(共12小题,每小题5分,共60分)1.化简的值是()A.B.C.D.2.已知,并且是第二象限的角,那么的值等于()A.B.C.D.3.设角属于第二象限,且,则角属于()A.第一象限B.第二象限C.第三象限D.第四象限4.的值()A.小于B.大于C.等于D.不存在5.函数f(x)=2cos()(x∈R)的最小正周期为()A.B.πC.2πD.4π6.若点(sin,cos)在角α的终边上,则sinα的值为()A.B.C.D.7.若sin(π﹣α)=﹣,且a∈(π,),则sin(+)=()A.﹣B.﹣C.D.8.已知,,那么的值是().A.B.C.D.9.函数y=sin(2x﹣)在区间[﹣,π]的简图是()A.B.C.D.10.函数f(x)=sin(x+)的图象关于()A.原点对称B.y轴对称C.直线x=对称D.直线x=﹣对称11.已知,,那么().A.B.C.D.12.将函数的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移个单位,得到的图象对应的僻析式是()A.B.C.D.二、填空题:(本大题共4小题,每小题5分,共20分)13.设扇形的周长为,面积为,则扇形的圆心角的弧度数是。14.函数的单调递增区间是___________________________.15.若函数f(x)=tan(ωx+)(ω>0)的最小正周期为2π,则ω=;f()=.16.给出下列五个命题:①函数的一条对称轴是x=;②函数y=tanx的图象关于点(,0)对称;③正弦函数在第一象限为增函数;以上三个命题中正确的有(填写所有正确命题的序号)三、解答题:(本题共6小题,共70分,解答过程应写出文字说明,证明过程或演算步骤)17.(10分)(1)已知sinα=,求tan(α+π)+的值.18.已知,求下列各式的值:(1);(2).19.求函数y=sin(x+),x∈[-2π,2π]的单调区间。20.求函数y=tan的定义域、单调区间和对称中心.21.如图,某地一天从6时至14时的温度变化曲线近似满足函数.(Ⅰ)求这段时间的最大温差;(Ⅱ)写出这段曲线的函数解析式.22.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示.(Ⅰ)写出函数f(x)的最小正周期T及ω、φ的值;(Ⅱ)求函数f(x)在区间[﹣,]上的最大值与最小值.参考答案123456789101112DACADAABBBBC13.215.,17.解:∵sinα=>0,∴α为第一或第二象限角.当α是第一象限角时,cosα==,tan(α+π)+=tanα+=+==.当α是第二象限角时,cosα=﹣=﹣,原式==﹣.18.解:(1)函数,∴f(0)=3sin=.(2)由于f(x)以为最小正周期,∴=,∴ω=4,∴f(x)=3sin(4x+).(3)设,则=3sin(2α+),∴sin(2α+)=.再根据2α+∈(,),可得2α+=,∴α=.22.解:(I)根据函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的部分图象,可得=﹣,求得ω=2,∴最小正周期T==π.再根据五点法作图可得2•+φ=π,求得φ=.(II)由以上可得,f(x)=sin(2x+),在区间[﹣,]上,2x+∈[﹣,],sin(2x+)∈[﹣,1],当2x+=﹣时,即x=﹣,函数f(x)取得最小值为﹣.当2x+=时,即x=,函数f(x)取得最大值为1.