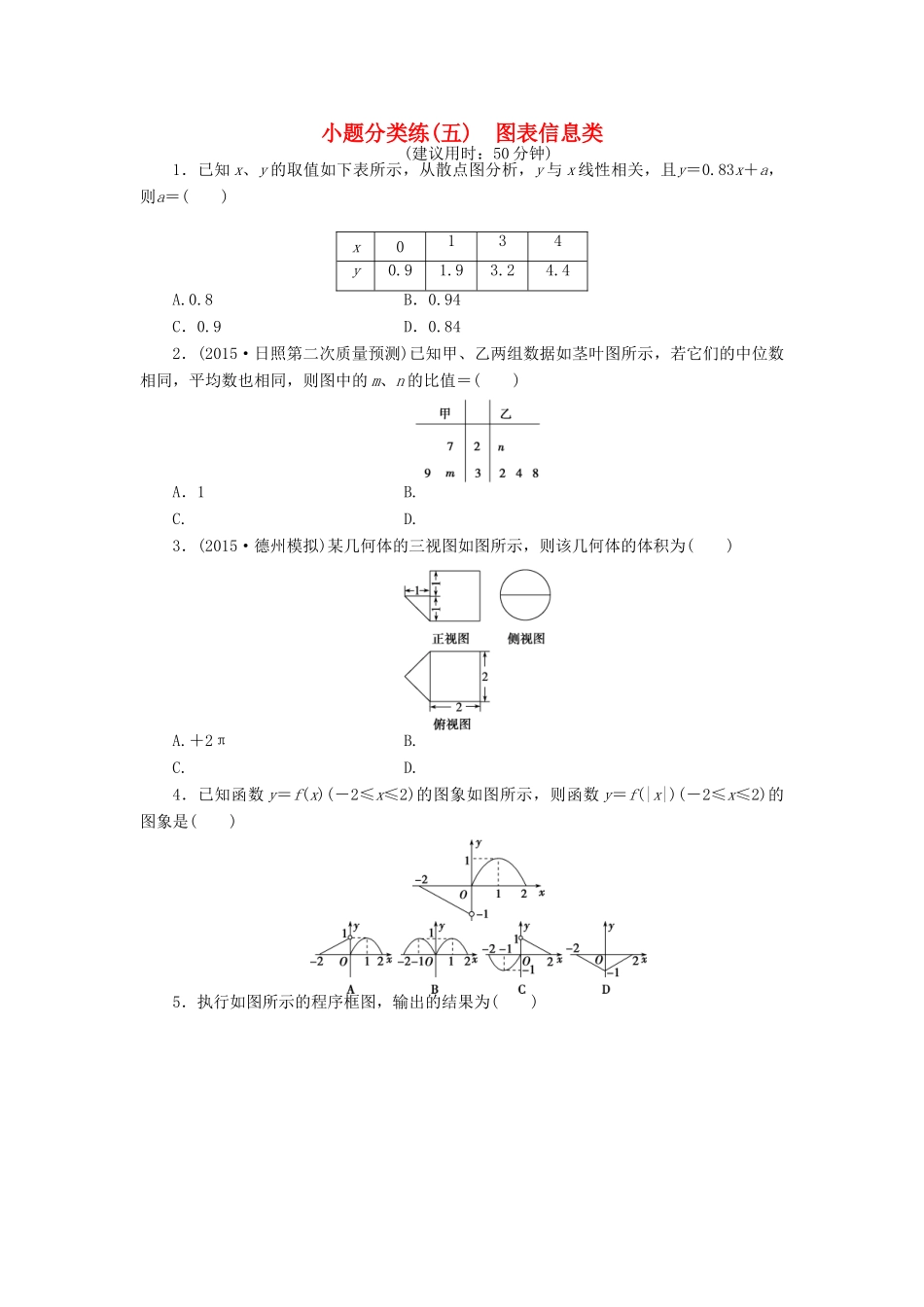
小题分类练(五)图表信息类(建议用时:50分钟)1.已知x、y的取值如下表所示,从散点图分析,y与x线性相关,且y=0.83x+a,则a=()x0134y0.91.93.24.4A.0.8B.0.94C.0.9D.0.842.(2015·日照第二次质量预测)已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的m、n的比值=()A.1B.C.D.3.(2015·德州模拟)某几何体的三视图如图所示,则该几何体的体积为()A.+2πB.C.D.4.已知函数y=f(x)(-2≤x≤2)的图象如图所示,则函数y=f(|x|)(-2≤x≤2)的图象是()5.执行如图所示的程序框图,输出的结果为()A.(-2,2)B.(-4,0)C.(-4,-4)D.(0,-8)6.(2015·烟台模拟)汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是()A.消耗1升汽油,乙车最多可行驶5千米B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油7.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是()A.{x|-1<x≤0}B.{x|-1≤x≤1}C.{x|-1<x≤1}D.{x|-1<x≤2}8.若对任意的x∈R,y=均有意义,则函数y=loga的大致图象是()9.某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为()甲乙原料限额A(吨)3212B(吨)128A.12万元B.16万元C.17万元D.18万元10.函数f(x)=的图象如图所示,则下列结论成立的是()A.a>0,b>0,c<0B.a<0,b>0,c>0C.a<0,b>0,c<0D.a<0,b<0,c<011.已知某地区中小学生人数和近视情况分别如图①和图②所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为________.12.如图,△ABC及其内部的点组成的集合记为D,P(x,y)为D中任意一点,则z=2x+3y的最大值为________.13.如图为函数f(x)=sin(ωx+φ)(ω>0)的部分图象,B、C分别为图象的最高点和最低点,若AB·BC=|AB|2,则ω=________.14.如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于________.15.(2015·东营模拟)如图所示,将正整数排成三角形数阵,每排的数称为一个群,从上到下顺次为第1群,第2群,…,第n群,…,第n群恰好有n个数,则第n群中n个数的和是________.小题分类练(五)图表信息类1.解析:选B.由题意,x==2,y==2.6,而样本的中心点(x,y)必在回归直线上,代入得2.6=0.83×2+a,从而有a=0.94.2.解析:选D.由茎叶图可知甲的数据为27、30+m、39,乙的数据为20+n、32、34、38.由此可知乙的中位数是33,所以甲的中位数也是33,所以m=3.由此可以得出甲的平均数为33,所以乙的平均数也为33,所以有=33,所以n=8,所以=,所以选D.3.解析:选B.由三视图可知,该几何体是一个圆柱和半个圆锥组合而成的几何体,其体积为π×12×2+×π×12×1=π.4.解析:选B.法一:由题意可得f(x)=所以y=f(|x|)=可知选B.法二:由函数f(x)的图象可知,函数在y轴右侧的图象在x轴上方,函数在y轴左侧的图象在x轴下方,而y=f(|x|)在x>0时的图象保持不变,因此排除C、D,由于y=f(|x|)是偶函数,函数y=f(|x|)在y轴右侧的图象与在y轴左侧的图象关于y轴对称,故选B.5.解析:选B.x=1,y=1,k=0,s=x-y=0,t=x+y=2,x=s=0,y=t=2,k=1,不满足k≥3;s=x-y=-2,t=x+y=2,x=-2,y=2,k=2,不满足k≥3;s=x-y=-4,t=x+y=0,x=-4,y=0,k=3,满足k≥3,输出的结果为(-4,0).6.解析:选D.根据图象知消耗1升汽油,乙车最多行驶里程大于5千米,故选项A错;以相同速度行驶时,甲车燃油效率最高,因此以相同速度行驶相同路程时,甲车消耗汽油最少,故选项B错;甲车以80千米/小时的速度行驶时燃油效率为10千米/升,行驶1小时...