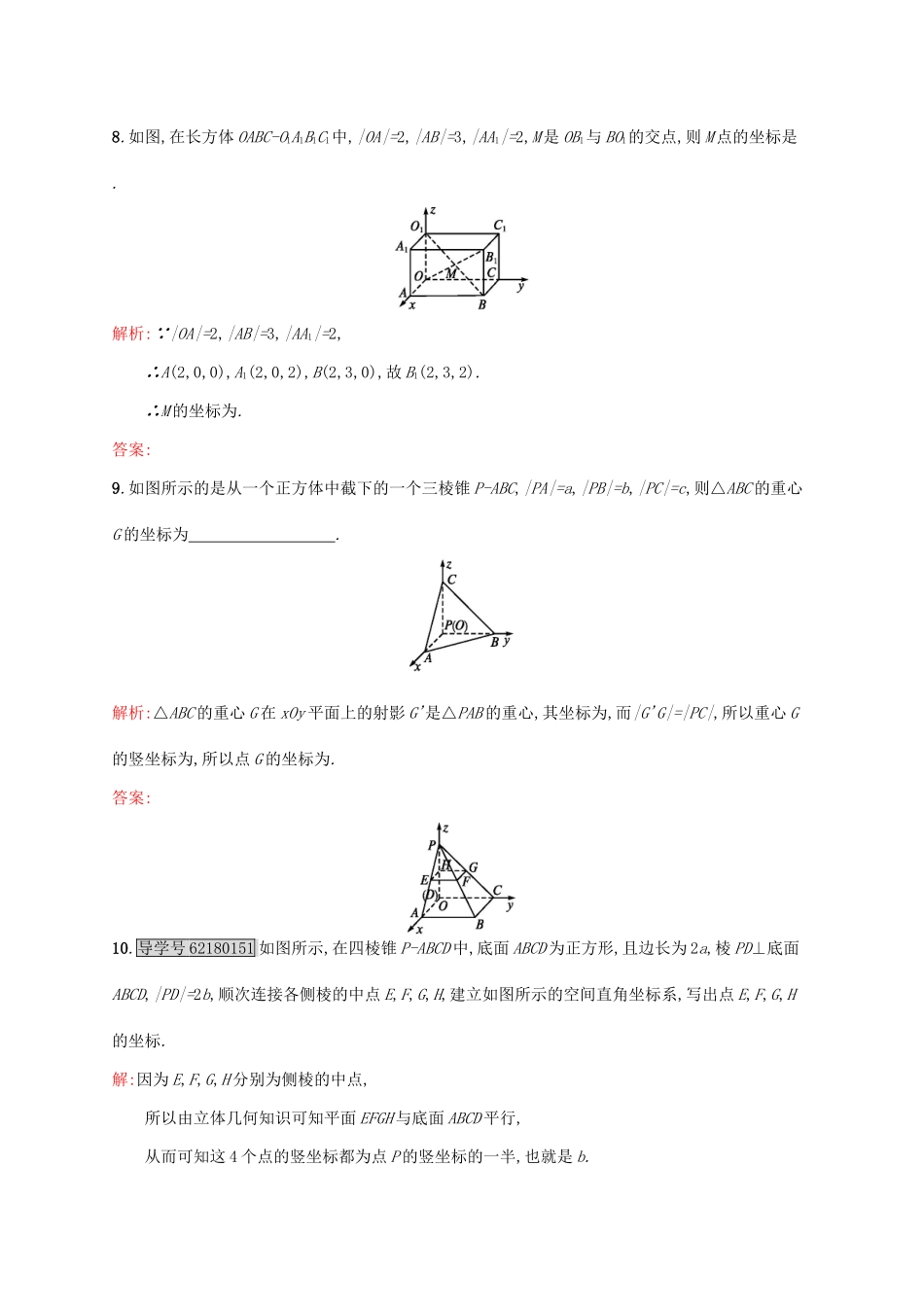
3.2空间直角坐标系中点的坐标1.在空间直角坐标系中,点A(1,-1,1)与点B(-1,-1,-1)关于()A.x轴对称B.y轴对称C.z轴对称D.原点对称解析:∵A,B两点的纵坐标相同,其他两个坐标均互为相反数,∴A,B两点关于y轴对称.答案:B2.已知A(4,1,3),B(2,-5,1),C是AB的中点,则C点的坐标为()A.(3,-2,2)B.(3,2,1)C.D.解析:设C(x,y,z),则x==3,y==-2,z==2,即C(3,-2,2).答案:A3.导学号62180150在空间直角坐标系中,已知点P(1,),过点P作yOz平面的垂线PQ,则垂足Q的坐标是()A.(0,,0)B.(0,)C.(1,0,)D.(1,,0)解析:根据空间直角坐标系的概念知yOz平面上的点Q的x坐标为0,y坐标、z坐标分别等于点P的y坐标,z坐标,所以垂足Q的坐标为(0,).答案:B4.如图,长方体ABCD-A1B1C1D1中,|OA|=3,|OC|=4,|OD1|=3,BC1与B1C相交于点P,则点P的坐标是()A.B.C.(3,4,3)D.解析:过P作BC的垂线交BC于M点,则M点是BC的中点,|PM|=,|MC|=,所以P.答案:D5.长方体ABCD-A1B1C1D1在空间直角坐标系中的位置如图所示,且AB=3,AD=2,AA1=1,则DD1C1C所在平面上点的坐标形式是()A.(0,-2,-1)B.(x,-2,z)C.(-3,-2,-1)D.(-3,y,z)解析:DD1C1C所在的平面平行于平面xOz,且与平面xOz的距离为2,平面DD1C1C上任意一点的y轴坐标都是-2,而x轴和z轴坐标可取任意实数.答案:B6.已知空间直角坐标系中有一点M(x,y,z)满足x>y>z,且x+y+z=0,则点M的位置是()A.一定在xOy平面上B.一定在yOz平面上C.一定在xOz平面上D.可能在xOz平面上解析:因为x>y>z,且x+y+z=0,所以x>0,z<0,y有可能为0,所以点M可能在xOz平面上.答案:D7.已知正四棱柱OABC-A1B1C1D1,若A(0,0,0),B(2,0,0),D(0,2,0),A1(0,0,5),则C1的坐标为.解析:由已知得正四棱柱的底面边长为2,高为5,所以C1的坐标为(2,2,5).答案:(2,2,5)8.如图,在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=2,M是OB1与BO1的交点,则M点的坐标是.解析:∵|OA|=2,|AB|=3,|AA1|=2,∴A(2,0,0),A1(2,0,2),B(2,3,0),故B1(2,3,2).∴M的坐标为.答案:9.如图所示的是从一个正方体中截下的一个三棱锥P-ABC,|PA|=a,|PB|=b,|PC|=c,则△ABC的重心G的坐标为.解析:△ABC的重心G在xOy平面上的射影G'是△PAB的重心,其坐标为,而|G'G|=|PC|,所以重心G的竖坐标为,所以点G的坐标为.答案:10.导学号62180151如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,且边长为2a,棱PD⊥底面ABCD,|PD|=2b,顺次连接各侧棱的中点E,F,G,H,建立如图所示的空间直角坐标系,写出点E,F,G,H的坐标.解:因为E,F,G,H分别为侧棱的中点,所以由立体几何知识可知平面EFGH与底面ABCD平行,从而可知这4个点的竖坐标都为点P的竖坐标的一半,也就是b.由H为DP的中点得H(0,0,b).因为E在底面上的射影为AD的中点,所以点E的横坐标和纵坐标分别为a和0.所以E(a,0,b).同理G(0,a,b).因为F在坐标平面xOz和yOz上的射影分别为E和G,所以F的横坐标与E的横坐标相同,是a,F的纵坐标与G的纵坐标相同,为a.又F的竖坐标为b,所以F(a,a,b).11.如图所示,AF,DE分别是圆O、圆O1的直径,AD与两圆所在的平面均垂直,|AD|=8,BC是☉O的直径,|AB|=|AC|=6,OE∥AD,试建立适当的空间直角坐标系,求出点A,B,C,D,E,F的坐标.解:因为AD与两圆所在的平面均垂直,OE∥AD,所以OE⊥平面ABC.又AF⫋平面ABC,BC⫋平面ABC,所以OE⊥AF,OE⊥BC.又BC是圆O的直径,所以OB=OC.又|AB|=|AC|=6,所以OA⊥BC,|BC|=6.所以|OA|=|OB|=|OC|=|OF|=3.如图所示,以O为原点,以OB,OF,OE所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,所以A(0,-3,0),B(3,0,0),C(-3,0,0),D(0,-3,8),E(0,0,8),F(0,3,0).12.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是D1D,BD的中点,G在棱CD上,且CG=CD,H为C1G的中点,试建立适当的直角坐标系,写出点E,F,G,H的坐标.解:以D为坐标原点,DA所在直线为x轴,DC所在直线为y轴,DD1所在直线为z轴,建立如图所示的空间直角坐标系.∵点E在z轴上,且为D1D的中点,∴点E坐标为.过点F作FM⊥AD,FN⊥DC,则|FM|=|FN|=,故点F坐标为.点G在y轴上,又|GD|=,故点G坐标为.过点H作HK⊥CG于点K,由于点H为C1G的中点,∴|HK|=,|CK|=.∴|DK|=.故点H的坐标为.