高中数学 专题强化训练7 概率（含解析）北师大版必修第一册-北师大版高一第一册数学试题VIP免费

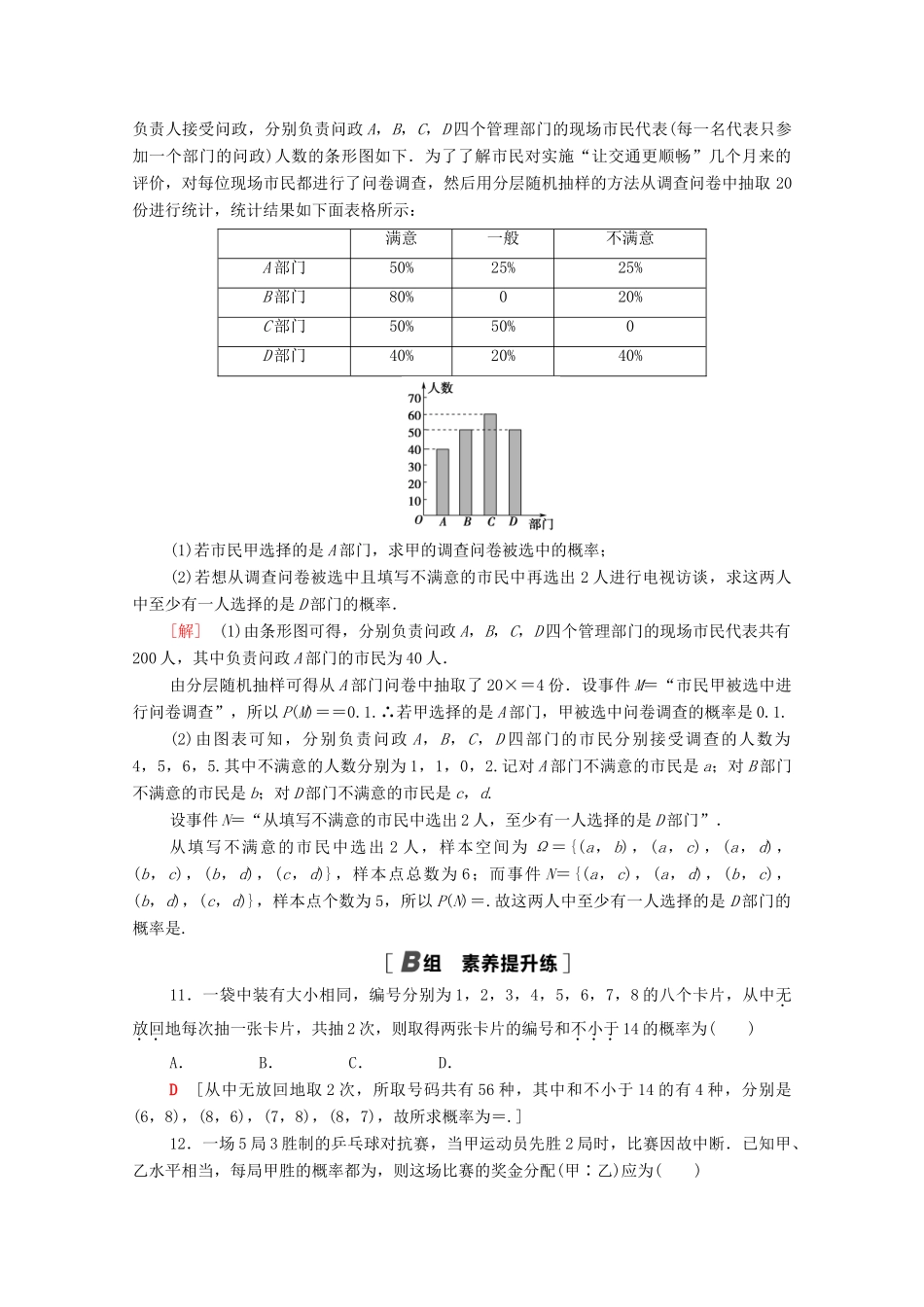
专题强化训练(七)概率(建议用时：40分钟)一、选择题1．把黑、红、白3张纸牌分给甲、乙、丙三人，则事件“甲分得红牌”与“乙分得红牌”是()A．对立事件B．互斥但不对立事件C．不可能事件D．必然事件B[根据题意，把黑、红、白3张纸牌分给甲、乙、丙三人，事件“甲分得红牌”与“乙分得红牌”不会同时发生，故两者是互斥事件，但除了“甲分得红牌”与“乙分得红牌”之外，还有“丙分得红牌”，故两者不是对立事件，所以事件“甲分得红牌”与“乙分得红牌”是互斥但不对立事件．]2．小明家的晚报在下午5：30～6：30任何一个时间随机地被送到，他们一家人在下午6：00～7：00任何一个时间随机地开始晚餐．为了计算晚报在晚餐开始之前被送到的概率，某小组借助随机数表的模拟方法来计算概率，他们的具体做法是将每个1分钟的时间段看作个体进行编号，5：30～5：31编号为01，5：31～5：32编号为02，依此类推，6：59～7：00编号为90.在随机数表中每次选取一个四位数，前两位表示晚报时间，后两位表示晚餐时间，如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义，视为这次读取的为无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右，读完第一行，再从左向右读第二行的顺序，读完下表，用频率估计晚报在晚餐开始之前被送到的概率为()78401160505431398082773250343682482940524201627756785188685402008650758401367655A.B．C．D．A[按要求读取到一下共9个数据：116050543139503436824052567851880136；其中晚报到达时间早于晚餐时间的是11605054313936824052567851880136共8个数据．∴晚报在晚餐开始之前被送到的概率为.故选A.]3．甲、乙、丙三人在3天节假日中值班，每人值班1天，则甲排在乙的前面值班的概率是()A．B．C．D．D[甲、乙、丙三人在3天中值班的情况为甲，乙，丙；甲，丙，乙；丙，甲，乙；丙，乙，甲；乙，甲，丙；乙，丙，甲共6种，其中符合题意的有3种，故所求概率为.]4．从{a，b，c，d，e}的所有子集中任取一个，这个集合恰是集合{a，b，c}子集的概率是()A．B．C．D．C[符合要求的是∅，{a}，{b}，{c}，{a，b}，{a，c}，{b，c}，{a，b，c}共8个，而集合{a，b，c，d，e}共有子集25＝32个，∴P＝.]5．先后抛掷两颗骰子，设出现的点数之和是12，11，10的概率依次是P1，P2，P3，则()A．P1＝P2＜P3B．P1＜P2＜P3C．P1＜P2＝P3D．P3＝P2＜P1B[先后抛掷两颗骰子的点数共有36个样本点：(1，1)，(1，2)，(1，3)，…，(6，6)，并且每个样本点都是等可能发生的．而点数之和为12的只有1个：(6，6)；点数之和为11的有2个：(5，6)，(6，5)；点数之和为10的有3个：(4，6)，(5，5)，(6，4)，故P1＜P2＜P3.]二、填空题6．一个袋子中有5个红球，3个白球，4个绿球，8个黑球，如果随机地摸出一个球，记A＝{摸出黑球}，B＝{摸出白球}，C＝{摸出绿球}，D＝{摸出红球}，则P(A)＝________；P(B)＝________；P(C＋D)＝________．[由古典概型的算法可得P(A)＝＝，P(B)＝，P(C＋D)＝P(C)＋P(D)＝＋＝.]7．若A，B是相互独立事件，且P(A)＝，P(B)＝，则P(A)＝________，P()＝________．[因为P(A)＝，P(B)＝，所以P()＝1－P(A)＝1－＝，P()＝1－＝.因为A，B相互独立，∴A与，与相互独立，∴P(A)＝P(A)P()＝×＝，P()＝P()P()＝×＝.]8．下课以后，教室里最后还剩下2位男同学，2位女同学，如果没有2位同学一块儿走，则第2位走的是男同学的概率是________．[已知有2位女同学和2位男同学，所有走的可能顺序有(女，女，男，男)，(女，男，女，男)，(女，男，男，女)，(男，男，女，女)，(男，女，男，女)，(男，女，女，男)，所以第2位走的是男同学的概率是P＝＝.]三、解答题9．同时抛掷1角、5角和1元的三枚硬币，计算：(1)恰有一枚出现正面的概率；(2)至少有两枚出现正面的概率．[解]试验的样本空间为Ω＝{(正，正，正)，(正，正，反)，(正，反，正)，(反，正，正)，(正，反，反)，(反，正，反)，(反，反，正)，(反，反，反)}，样本点总数为8.(1)用A表示“恰有一枚出现正面”这一事件：则A＝{(正，反，反)，(反，反，正)，(反，正，反)}．因此P(A)＝.(2)用B表示“至少有两枚出...