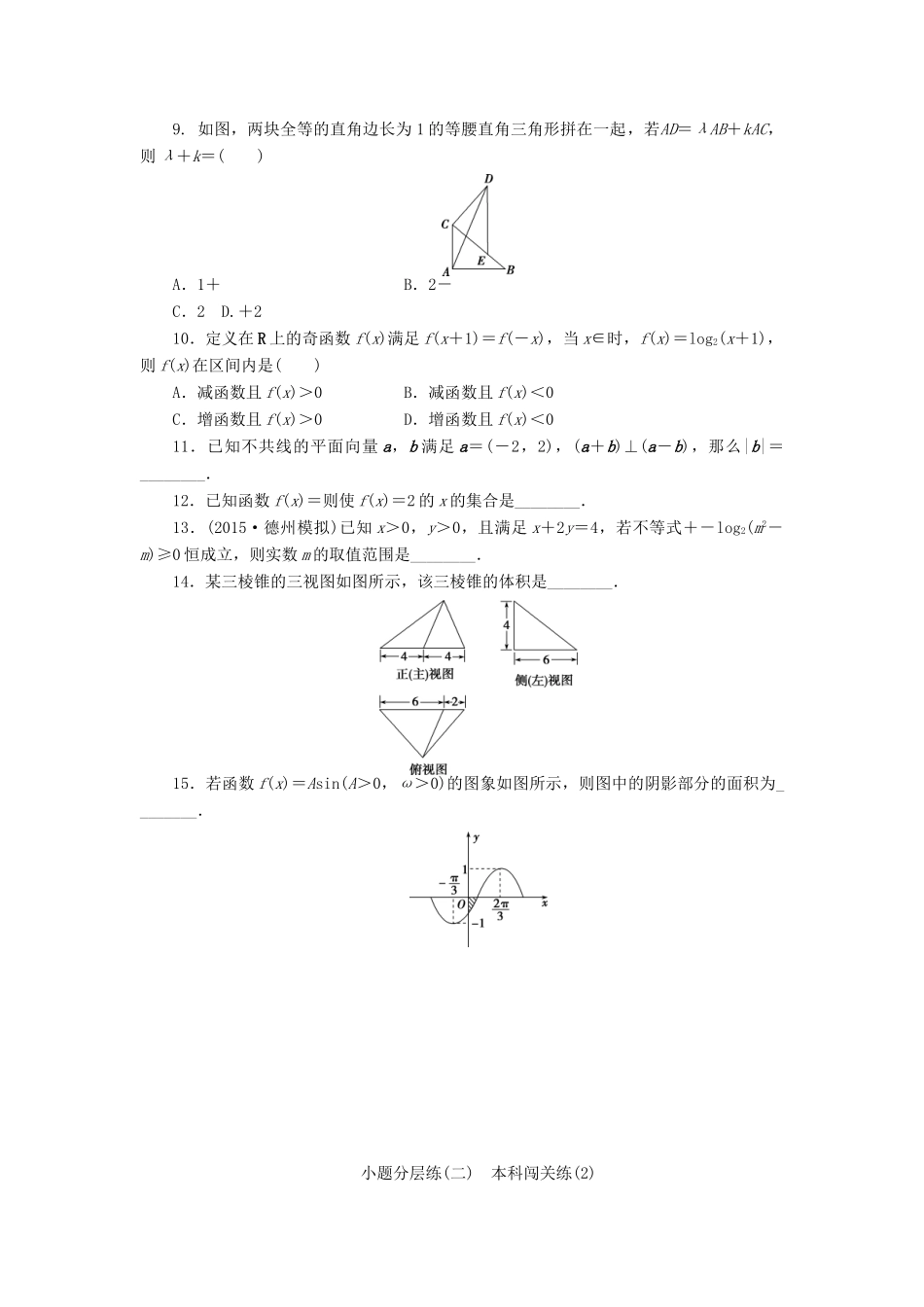
小题分层练(二)本科闯关练(2)(建议用时:50分钟)1.已知集合M={x|y=lg(2x-x2)},N={x|x2+y2=1},则M∩N=()A.[-1,2)B.(0,1)C.(0,1]D.∅2.已知双曲线C:-=1(a>0,b>0)的离心率e=,且其右焦点为F2(5,0),则双曲线C的标准方程为()A.-=1B.-=1C.-=1D.-=13.(2015·临沂双基过关考试)设α,β,γ为不同的平面,m,n为不同的直线,则m⊥β的一个充分条件是()A.α⊥β,α∩β=n,m⊥nB.α∩γ=m,α⊥γ,β⊥γC.α⊥β,β⊥γ,m⊥αD.n⊥α,n⊥β,m⊥α4.已知sinα+cosα=,则tanα+的值为()A.-1B.-2C.D.25.(2015·聊城模拟)高三(3)班共有学生56人,座号分别为1,2,3,…,56,现根据座号,用系统抽样的方法,抽取一个容量为4的样本.已知3号、17号、45号同学在样本中,那么样本中还有一个同学的座号是()A.30B.31C.32D.336.设复数z=(x-1)+yi(x,y∈R),若|z|≤1,则y≥x的概率为()A.+B.+C.-D.-7.(2015·威海模拟)已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.下面是一个算法的程序框图,当输入的值为25时,则输出的结果为()A.4B.5C.6D.78.将甲、乙等5名交警分配到三个不同路口疏导交通,每个路口至少一人,且甲、乙在同一路口的分配方案共有()A.18种B.24种C.36种D.72种9.如图,两块全等的直角边长为1的等腰直角三角形拼在一起,若AD=λAB+kAC,则λ+k=()A.1+B.2-C.2D.+210.定义在R上的奇函数f(x)满足f(x+1)=f(-x),当x∈时,f(x)=log2(x+1),则f(x)在区间内是()A.减函数且f(x)>0B.减函数且f(x)<0C.增函数且f(x)>0D.增函数且f(x)<011.已知不共线的平面向量a,b满足a=(-2,2),(a+b)⊥(a-b),那么|b|=________.12.已知函数f(x)=则使f(x)=2的x的集合是________.13.(2015·德州模拟)已知x>0,y>0,且满足x+2y=4,若不等式+-log2(m2-m)≥0恒成立,则实数m的取值范围是________.14.某三棱锥的三视图如图所示,该三棱锥的体积是________.15.若函数f(x)=Asin(A>0,ω>0)的图象如图所示,则图中的阴影部分的面积为________.小题分层练(二)本科闯关练(2)1.解析:选C.由2x-x2>0,解得0<x<2,故M={x|0<x<2},又N={x|-1≤x≤1},因此M∩N=(0,1].2.解析:选C.因为e==,F2(5,0),所以c=5,所以a=4,b2=c2-a2=9,所以双曲线C的标准方程为-=1.3.解析:选D.A不对,m可能在平面β内,也可能与β平行;B,C不对,满足条件的m和β可能相交,也可能平行;D对,由n⊥α,n⊥β可知α∥β,结合m⊥α知m⊥β,故选D.4.解析:选D.依题意得(sinα+cosα)2=1+2sinαcosα=2,所以2sinαcosα=1,从而tanα+===2,故选D.5.解析:选B.抽取容量为4的样本,则要将总体分为4组,每组有14人,由题意可知抽取的座号分别为3,17,31,45,故选B.6.解析:选D.|z|=≤1,即(x-1)2+y2≤1,表示的是圆及其内部,如图所示.当|z|≤1时,y≥x表示的是图中阴影部分,其面积为S=π×12-×1×1=.又圆的面积为π,根据几何概型公式得概率P==-.7.解析:选B.输入n=25时,i=2,MOD(25,2)=0不成立;i=2+1=3,MOD(25,3)=0不成立;i=3+1=4,MOD(25,4)=0不成立;i=4+1=5,MOD(25,5)=0成立,故输出的结果为5.8.解析:选C.不同的分配方案可分为以下两种情况:①甲、乙两人在一个路口,其余三人分配在另外的两个路口,其不同的分配方案有CA=18种;②甲、乙所在路口分配三人,另外两个路口各分配一个人,其不同的分配方案有CA=18种.由分类加法计数原理可知不同的分配方案共有18+18=36种.9.解析:选A.AD=AC+CD=AC+(ED-EC)=AC+=AC+AC-(AC-AB)=AC+AB.所以λ=,k=1+,所以λ+k=1+.故选A.10.解析:选B.由f(x+1)=f(-x)可知,函数f(x)的图象关于直线x=对称,又函数f(x)为奇函数,故f(x+1)=f(-x)=-f(x),所以f(x+2)=f(x),即函数f(x)的周期为2,又当x∈时,f(x)=log2(x+1),故可得到函数f(x)的大致图象如图所示.由图象可知选B.11.解析:由(a+b)⊥(a-b)可知(a...