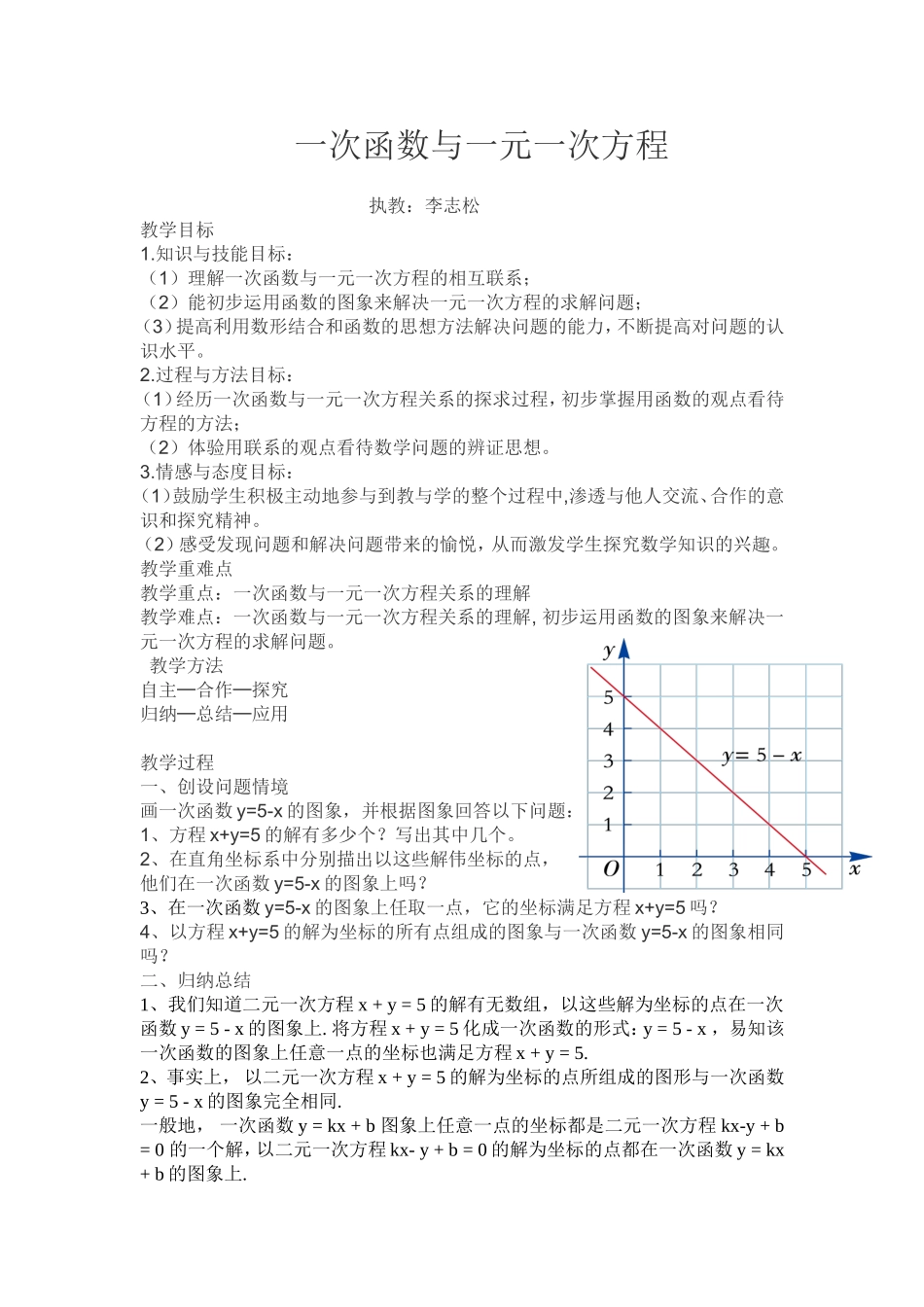
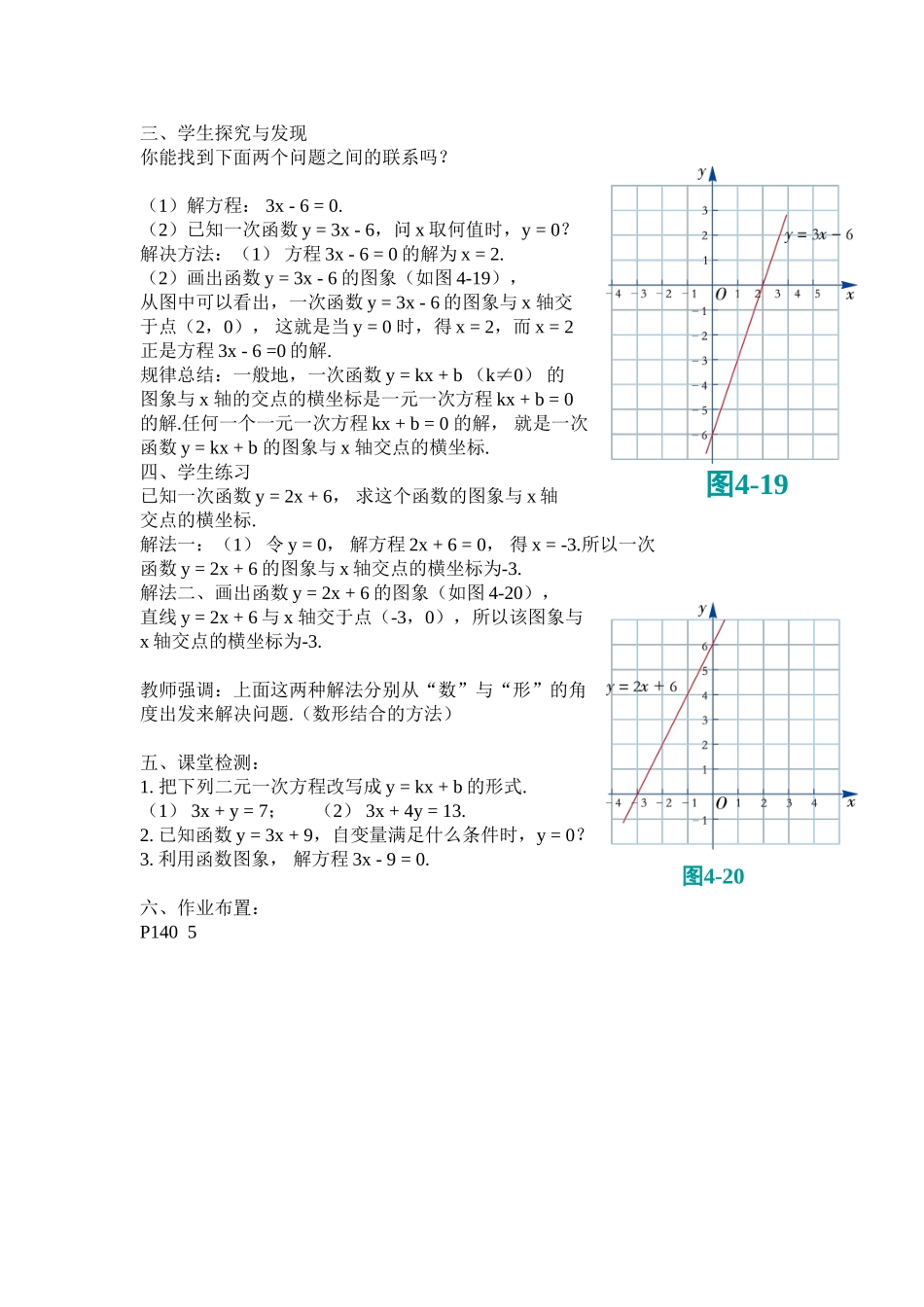
一次函数与一元一次方程执教:李志松教学目标1.知识与技能目标:(1)理解一次函数与一元一次方程的相互联系;(2)能初步运用函数的图象来解决一元一次方程的求解问题;(3)提高利用数形结合和函数的思想方法解决问题的能力,不断提高对问题的认识水平。2.过程与方法目标:(1)经历一次函数与一元一次方程关系的探求过程,初步掌握用函数的观点看待方程的方法;(2)体验用联系的观点看待数学问题的辨证思想。3.情感与态度目标:(1)鼓励学生积极主动地参与到教与学的整个过程中,渗透与他人交流、合作的意识和探究精神。(2)感受发现问题和解决问题带来的愉悦,从而激发学生探究数学知识的兴趣。教学重难点教学重点:一次函数与一元一次方程关系的理解教学难点:一次函数与一元一次方程关系的理解,初步运用函数的图象来解决一元一次方程的求解问题。教学方法自主─合作─探究归纳─总结─应用教学过程一、创设问题情境画一次函数y=5-x的图象,并根据图象回答以下问题:1、方程x+y=5的解有多少个?写出其中几个。2、在直角坐标系中分别描出以这些解伟坐标的点,他们在一次函数y=5-x的图象上吗?3、在一次函数y=5-x的图象上任取一点,它的坐标满足方程x+y=5吗?4、以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5-x的图象相同吗?二、归纳总结1、我们知道二元一次方程x+y=5的解有无数组,以这些解为坐标的点在一次函数y=5-x的图象上.将方程x+y=5化成一次函数的形式:y=5-x,易知该一次函数的图象上任意一点的坐标也满足方程x+y=5.2、事实上,以二元一次方程x+y=5的解为坐标的点所组成的图形与一次函数y=5-x的图象完全相同.一般地,一次函数y=kx+b图象上任意一点的坐标都是二元一次方程kx-y+b=0的一个解,以二元一次方程kx-y+b=0的解为坐标的点都在一次函数y=kx+b的图象上.三、学生探究与发现你能找到下面两个问题之间的联系吗?(1)解方程:3x-6=0.(2)已知一次函数y=3x-6,问x取何值时,y=0?解决方法:(1)方程3x-6=0的解为x=2.(2)画出函数y=3x-6的图象(如图4-19),从图中可以看出,一次函数y=3x-6的图象与x轴交于点(2,0),这就是当y=0时,得x=2,而x=2正是方程3x-6=0的解.规律总结:一般地,一次函数y=kx+b(k≠0)的图象与x轴的交点的横坐标是一元一次方程kx+b=0的解.任何一个一元一次方程kx+b=0的解,就是一次函数y=kx+b的图象与x轴交点的横坐标.四、学生练习已知一次函数y=2x+6,求这个函数的图象与x轴交点的横坐标.解法一:(1)令y=0,解方程2x+6=0,得x=-3.所以一次函数y=2x+6的图象与x轴交点的横坐标为-3.解法二、画出函数y=2x+6的图象(如图4-20),直线y=2x+6与x轴交于点(-3,0),所以该图象与x轴交点的横坐标为-3.教师强调:上面这两种解法分别从“数”与“形”的角度出发来解决问题.(数形结合的方法)五、课堂检测:1.把下列二元一次方程改写成y=kx+b的形式.(1)3x+y=7;(2)3x+4y=13.2.已知函数y=3x+9,自变量满足什么条件时,y=0?3.利用函数图象,解方程3x-9=0.六、作业布置:P1405图4-19图4-20