等差数列求和1VIP免费

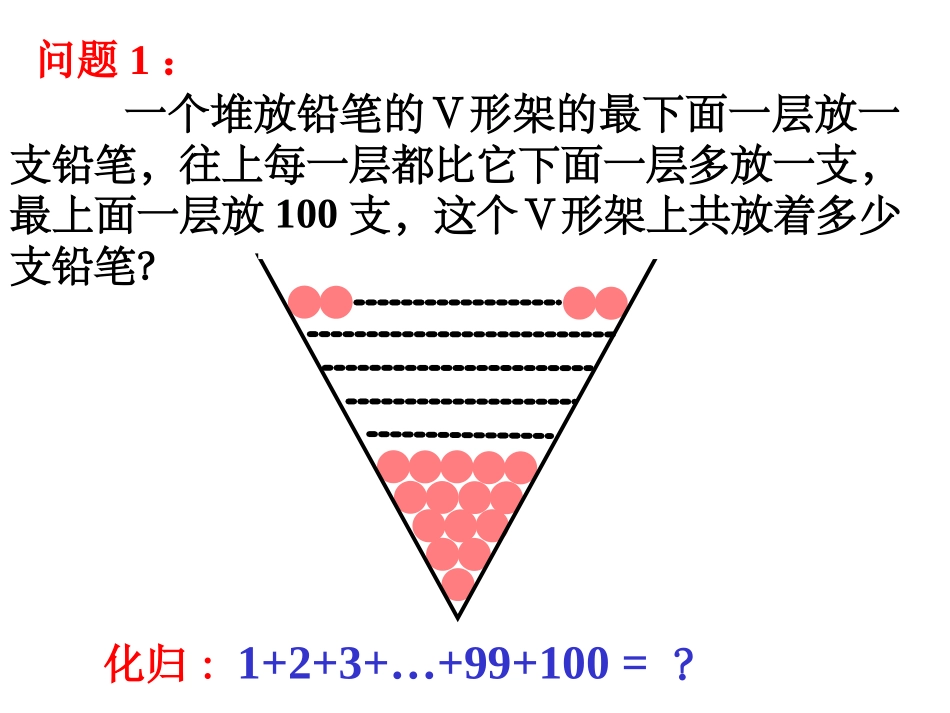
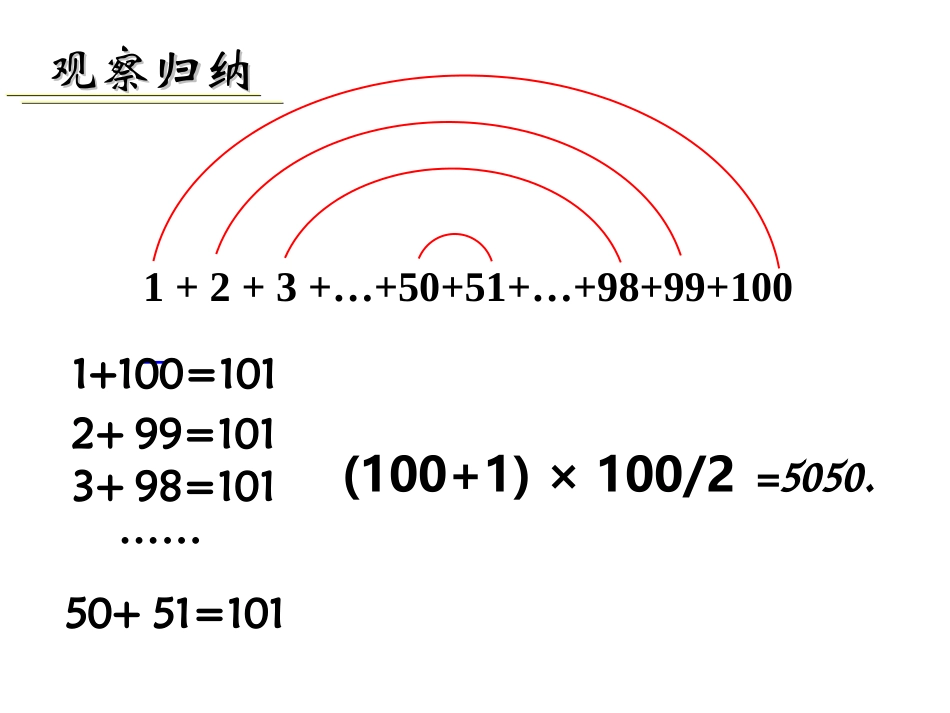
2.3.1等差数列的前n项和(1)一个堆放铅笔的Ｖ形架的最下面一层放一支铅笔，往上每一层都比它下面一层多放一支，最上面一层放100支，这个Ｖ形架上共放着多少支铅笔？化归:1+2+3+…+99+100=？问题1：1+2+3+…+50+51+…+98+99+1001+100=1012+99=1013+98=101……50+51=101(100+1)×100/2观察归纳观察归纳=5050.高斯高斯(1777(1777年年-1855-1855年年))德国著名数学家德国著名数学家学校为美化校园，决定在道路旁摆放盆景.从校门口取出花盆到距校门1米处开始摆放，每隔1米摆放一盆，学生小王每次拿两盆，若要完成摆放30盆的任务，最后返回校门处，问小王走过的总路程是多少？问题2：4m8m12m60m化归:4+8+12+…+60=？4+8+12+…+52+56+60=？15(460)152S15480.S60+56+52+…+12+8+4=？答：小王走过的总路程是480米.4m8m56m60mS15S151239899100?1009998321?100(1100)1002S5050.S100S100如图，工地有上一堆圆木，从上到下每层的数目分别为1，2，3，……，10。问共有多少根圆木？请用简便的方法计算。设等差数列{an}的前n项和为Sn,即：Sn=a1+a2+a3+…+an-2+an-1+anSn=an+an-1+an-2+…+a3+a2+a1两式相加得:2Sn=(a1+an)×n12132......nnnaaaaaa2)(1nnaanS1.1.公式推导公式推导算法：算法：倒序相加倒序相加法法()...[(1)]nnnnSaadand111()...[(1)]nSaadand12()nnSnaa两式相加得:1()12nnnaaS公式：1(1)naand1(1)22nnnSnad公式：推导公式(教材)：前n和公式：共5个量，由三个公式联系，知三可求二.通项公式：1()12nnnaaS公式：1(1)22nnnSnad公式：1(1)naand例1、计算：（1）1+2+3+…+n=________.（2）1+3+5+…+(2n-1)=________.（3）2+4+6+…+2n=__________.(1)2nn2n(1)nn例2等差数列-10，-6，-2，2，…前多少项的和为54？解：设题中的等差数列是｛an｝，前n项和为Sn则a1＝－10，d＝－6－（－10）＝4令＝54，由等差数列前n项和公式，得(1)10454.2nnn解得n1＝9，n2＝－3（舍去）因此,等差数列的前9项和是54方程思想知三求一nS例3在等差数列{an}中，，已知36)1(151252aaaa；求16S，已知20)2(6a.11S求(1)解:36)(2161aa.18161aa即2)(1616116aaS161125152aaaaaa21816.144(2)解:2)(1111111aaS2)(1166aa611a.2202)(1616116aaS例4已知一个等差数列的前10项的和为310,前20项的和是1220,由此可以确定其前n项和的公式吗?解：由题意知1220,3102010SS代入公式dnnnaSn2)1(1122019020310451011dada得:641da解得:.32nn62)1(4nnnSn故可以确定前n项和的公式.。元素的和的元素个数，并求这些且求集合例100,,72*mNnnmmM7100n得，由解：1007n7214满足此不等式的正整数n共有14个，所以集合M中的元素共有14个，从小到大可列为：7，7×2，7×3，7×4，…7×14即:7，14，21，28,…,98.98,7141aa其中2)987(1414S735答：集合M中共有14个元素，它们和等于735.这个数列是等差数列，例5.，，且，分别为项之和前，已知等差数列例432}{}{4nnTSTSnbannnnnn.1111的值求：ba2)(2)(11nnnnbbnaanTS解nnbbaa111111ba11111111bbaa211211bbaa2121TS432nnTSnn又67232121TS.67231111ba故例6.，，且，分别为项之和前，已知等差数列例432}{}{4nnTSTSnbannnnnn.1111的值求：ba解法2：21kS21(21)kkTkb由已知得：(21)kka2121kkkkaSbT11211121aSbT212321423.67例6.小结：1.掌握等差数列的两个求和公式及简单应用.2.回顾从特殊到一般，一般到特殊的研究方法.3.体会倒序相加的算法及数形结合的数学思想.课堂练习：教材45页练习课后作业2.教辅课时作业第16页2.3.1（一）4.预习教辅第32页~35页内容3.教辅第30页~第32页内容1.教材第46页习题2.3A组1~6