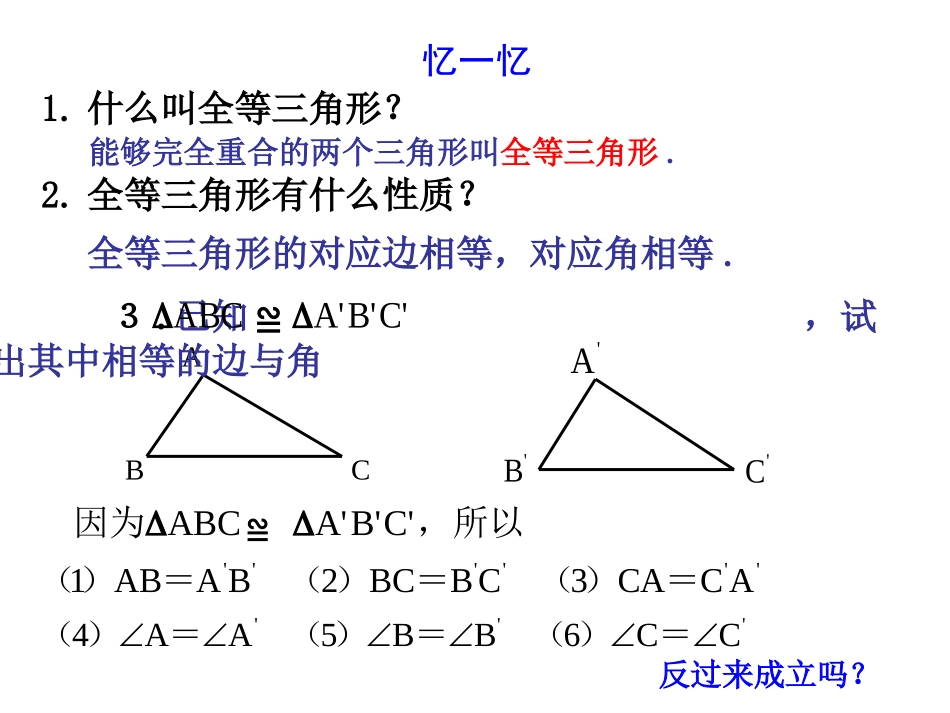
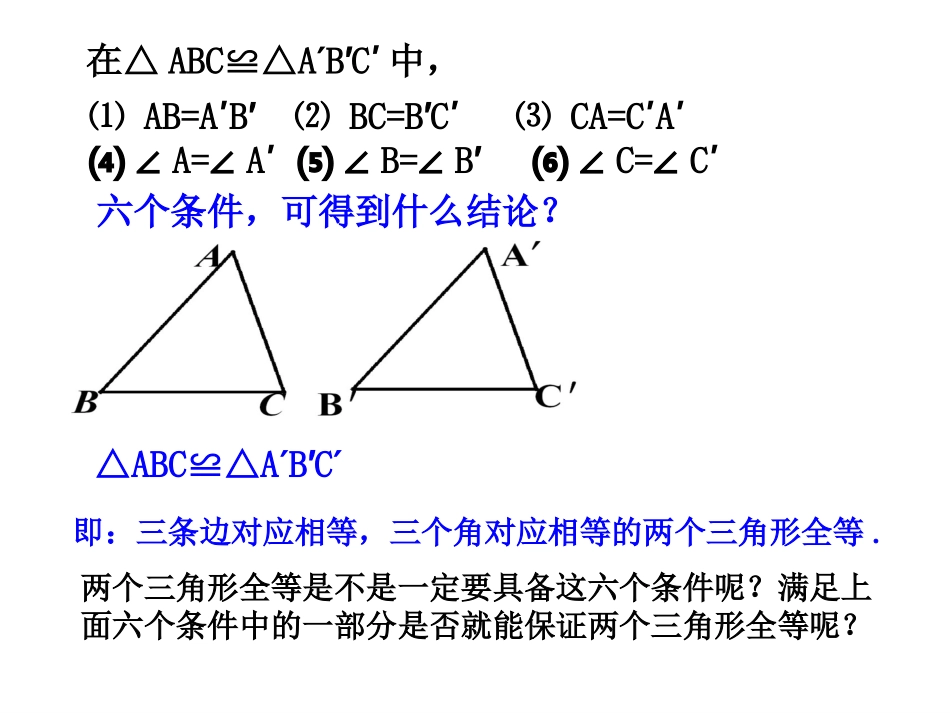
§12.2三角形全等的判定(第1课时)ABC1.什么叫全等三角形?能够完全重合的两个三角形叫全等三角形.2.全等三角形有什么性质?全等三角形的对应边相等,对应角相等.3.已知,试找出其中相等的边与角C'B'A'ABC≌''''''ACCA3CBBC2BAAB1=)(=)(=)('''CC6BB5AA4=)(=)(=)(,所以因为C'B'A'ABC≌'A'B'C忆一忆反过来成立吗?在△ABC≌△A′B′C′中,⑴AB=A′B′⑵BC=B′C′⑶CA=C′A′⑷∠A=∠A′⑸∠B=∠B′⑹∠C=∠C′六个条件,可得到什么结论?△ABC≌△A′B′C′即:三条边对应相等,三个角对应相等的两个三角形全等.两个三角形全等是不是一定要具备这六个条件呢?满足上面六个条件中的一部分是否就能保证两个三角形全等呢?1.有一条边相等的两个三角形不一定全等探究1:一个条件可以吗?探究1:一个条件可以吗?2.有一个角相等的两个三角形不一定全等结论:有一个条件相等不能保证两个三角形全等.6cm300有两个条件对应相等不能保证三角形全等.60o300不一定全等1.有两个角对应相等的两个三角形3.有一个角和一条边对应相等的两个三角形2.有两条边对应相等的两个三角形4cm6cm不一定全等30060o4cm6cm不一定全等30o6cm结论:两个条件可以吗?两个条件可以吗?探究2:三个条件呢?探究2:三个条件呢?如果给出三个条件画三角形,有哪几种可能的情况?1.三个角.2.三条边.3.两边一角.4.两角一边.结论:三个内角对应相等的三角形不一定全等.1.有三个角对应相等的两个三角形60o30030060o90o90o90o90o作法:1.画线段B′C′=BC.2.分别以B′,C′为圆心.BA,CA为半径画弧.两弧交于点A′.3.连接线段A′B′,A′C′.B′C′A′2.三边相等的两个三角形会全等吗?任意画一个△ABC.再画一个△A′B′C′.使A′B′=AB.B′C′=BC.C′A′=CA.把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?ABC三边对应相等的两个三角形全等.(简写成“边边边”或“SSS”)如何用符号语言来表达呢?∴∠A=∠A′∠B=∠B′∠C=∠C′AB=A′B′AC=A′C′BC=B′C′在△ABC和△A′B′C′中∴△ABC≌△A′B′C′注:这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理.∴△ABCADC△(SSS)例1已知:如图,AB=AD,BC=CD,求证:△ABCADC≌△ABCDACAC()≌AB=AD()BC=DC()证明:在△ABC和△ADC中=已知已知公共边判断两个三角形全等的推理过程,叫做证明三角形全等。分析:要证明△ABC≌△ADC,首先看这两个三角形的三条边是否对应相等。结论:从这题的证明中可以看出,证明是由已知出发,经过一步步的推理,最后推出结论正确的过程。①准备条件:证全等时要用的条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤:例1如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.求证:△ABD≌△ACD.ABCDABCD.CDBDBCD=的中点,是证明:ACDABD中,和在ADADCDBDACAB(公共边)=(已证)=(已知)=≌.SSSACDABD)((1)(2)∠BAD=∠CAD.(2)∠BAD=∠CAD.(2)由(1)得△ABDACD≌△,∴∠∠BAD=CAD.∠BAD=CAD.∠(全等三角形对应角相等)(全等三角形对应角相等)O′D′B′C′A′ODBCA用尺规作一个角等于已知角已知:∠AOB.求作:∠A′O′B′=∠AOB.作法:1.以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D.2.画一条射线O′A′.以点O′为圆心OC长为半径画弧.交O′A′于点C′.3.以点C′为圆心.CD长为半径画弧.与第2步中所画的弧交于点D′.4.过点D′画射线O′B′,则∠A′O′B′=∠AOB.工人师傅常用角尺平分一个任意角.做法如下:如图,AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC便是AOB的平分线.为什么?中,和解:在CNOCMOOMABNCCOCOCNCMONOM,=,=,=.AOBOC的平分线是.SSSCNOCMO)(≌.CONCOM=(全等三角形对应角相等)(已知)(已知)(公共边)CCBBDDAAFFEEDDBB证明: AD=FB∴AD+DB=FB+DB即AB=FD已知AC=FE,BC=DE,点A、D、...