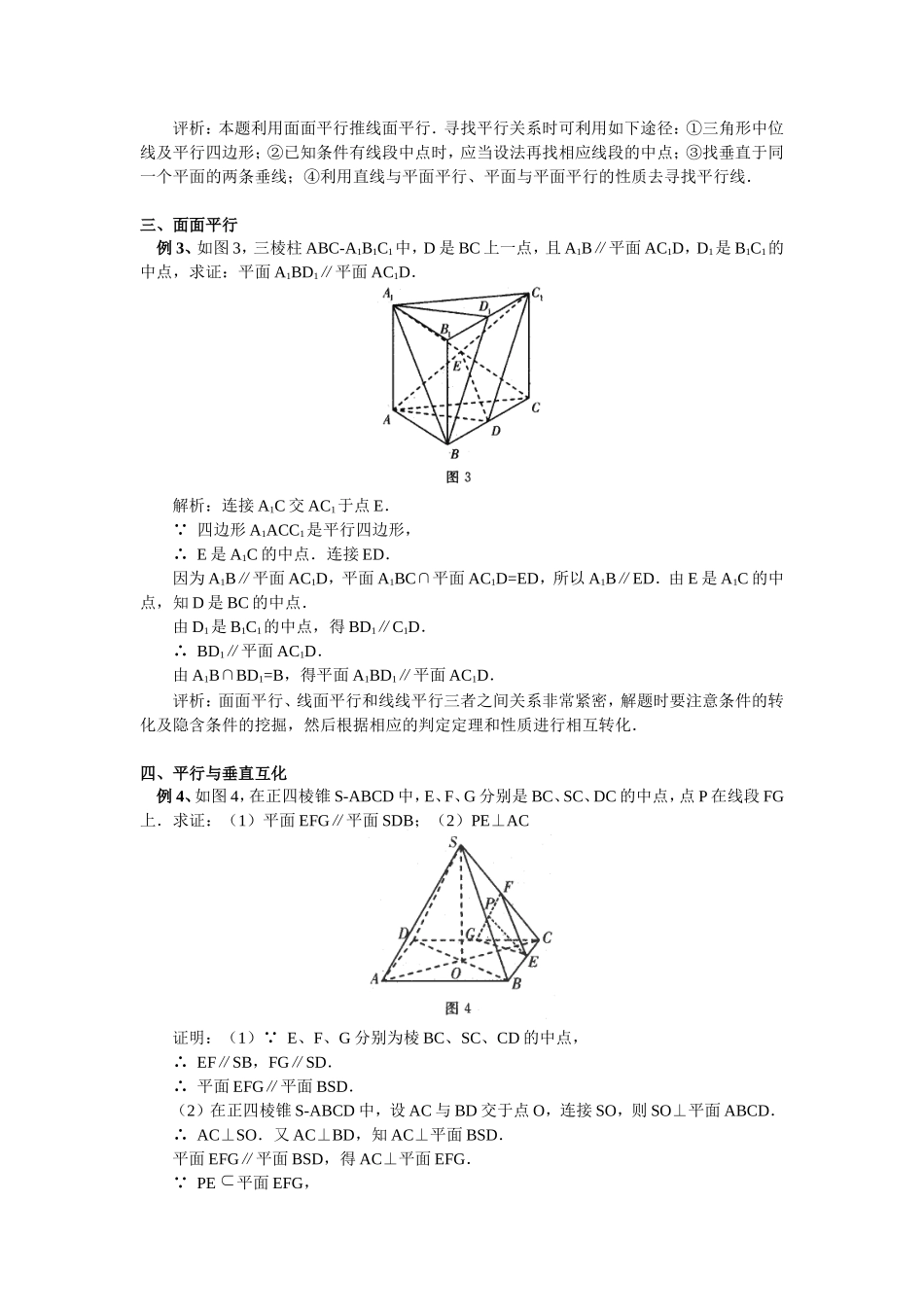
例析空间平行关系问题叶少蒙平行问题是高考考查的重点和热点之一,线线平行、线面平行、面面平行三者关系密切,可以相互转化.这种转化关系不仅是一种解题思想,更是一种解题策略.本文举例加以分析.一、线线平行例1、如图1,ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G、A、P作平面交平面BDM于GH.求证:AP∥GH.证明:连接AC,设AC交BD于O,连MO.∵四边形ABCD是平形四边形,∴O是AC的中点.M是PC的中点,可得MO∥PA.又MO平面BDM,PA平面BDM,所以PA∥平面BDM.又PA平面PAHG,且平面PAHG∩平面BDM=GH,所以AP∥GH.评析:本例先证线面平行,然后证线线平行,利用线面平行证明线线平行是一种重要的解题方法,这种互相之间的转化应灵活使用.二、线面平行例2、如图2,四棱锥P-ABCD,在底面菱形ABCD中,点E在PD上,且PE:ED=2:1,在PC上是否存在一点F,使BF∥平面AEC?证明你的结论.解析:当F是棱PC的中点时,BF∥平面AEC.下面给出证明.取PE的中点M,连接FM,则FM∥CE.∴FM∥平面AEC①.连接BM、BD,设BD∩AC=O,则O为BD的中点.∴BM∥OE.所以BM∥平面AEC②.又BM∩FM=M,由①②知,平面BFM∥平面AEC.又BF平面BFM,所以BF∥平面AEC.评析:本题利用面面平行推线面平行.寻找平行关系时可利用如下途径:①三角形中位线及平行四边形;②已知条件有线段中点时,应当设法再找相应线段的中点;③找垂直于同一个平面的两条垂线;④利用直线与平面平行、平面与平面平行的性质去寻找平行线.三、面面平行例3、如图3,三棱柱ABC-A1B1C1中,D是BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,求证:平面A1BD1∥平面AC1D.解析:连接A1C交AC1于点E.∵四边形A1ACC1是平行四边形,∴E是A1C的中点.连接ED.因为A1B∥平面AC1D,平面A1BC∩平面AC1D=ED,所以A1B∥ED.由E是A1C的中点,知D是BC的中点.由D1是B1C1的中点,得BD1∥C1D.∴BD1∥平面AC1D.由A1B∩BD1=B,得平面A1BD1∥平面AC1D.评析:面面平行、线面平行和线线平行三者之间关系非常紧密,解题时要注意条件的转化及隐含条件的挖掘,然后根据相应的判定定理和性质进行相互转化.四、平行与垂直互化例4、如图4,在正四棱锥S-ABCD中,E、F、G分别是BC、SC、DC的中点,点P在线段FG上.求证:(1)平面EFG∥平面SDB;(2)PE⊥AC证明:(1)∵E、F、G分别为棱BC、SC、CD的中点,∴EF∥SB,FG∥SD.∴平面EFG∥平面BSD.(2)在正四棱锥S-ABCD中,设AC与BD交于点O,连接SO,则SO⊥平面ABCD.∴AC⊥SO.又AC⊥BD,知AC⊥平面BSD.平面EFG∥平面BSD,得AC⊥平面EFG.∵PE平面EFG,∴PE⊥AC.评析:本题考查了平行与垂直的互化,利用线线平行面面平行,证明了第1问;利用面面平行线面垂直,证明了第2问.平行和垂直的互化体现了两种位置关系的重要性.