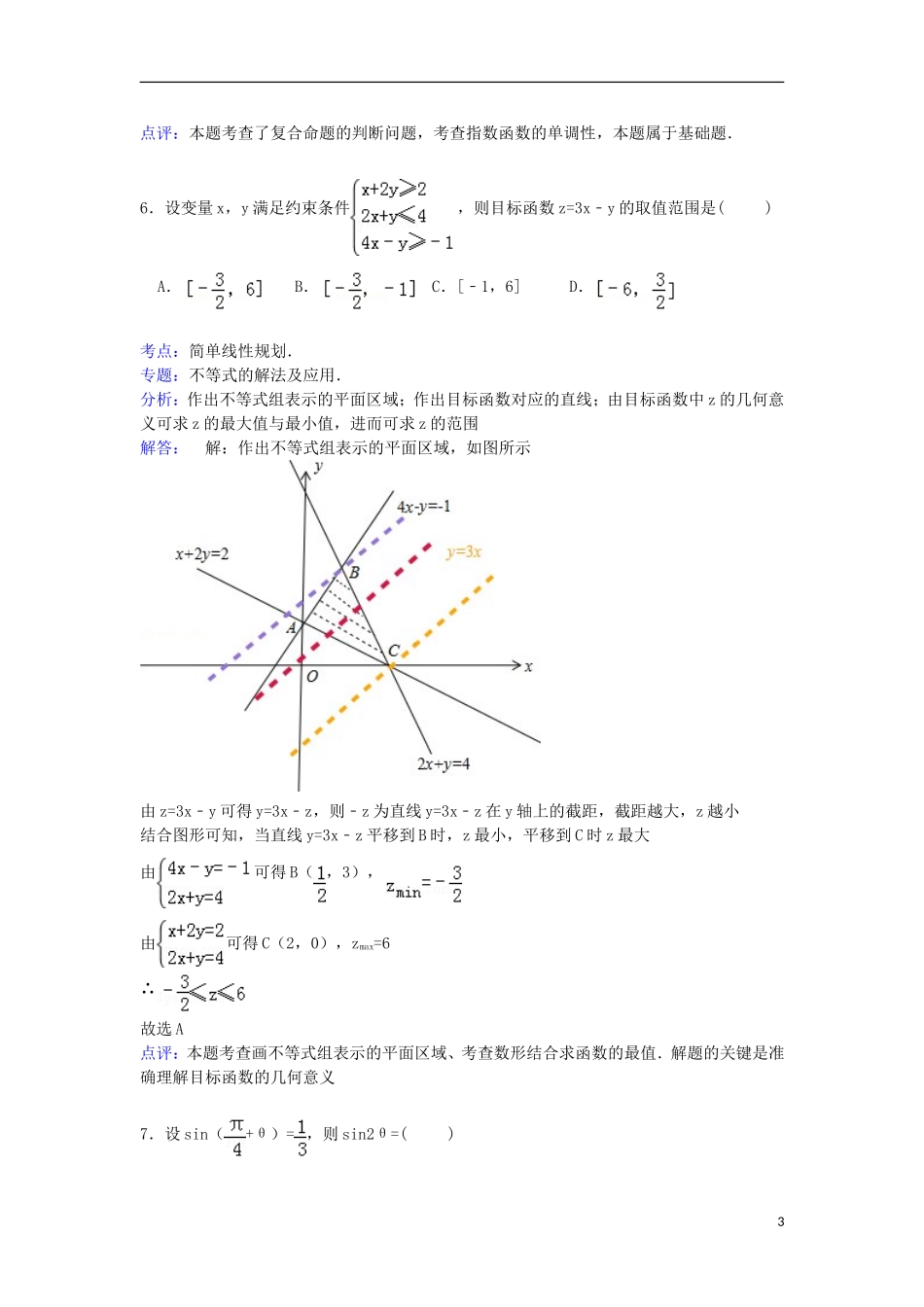
湖北省襄阳市优质高中联考2015届高考数学模拟试卷(文科)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合U={1,2,3,4,5,6,7},M={2,4,7},则∁UM=()A.UB.{1,2,6}C.{1,3,5,6}D.{1,3,5}考点:补集及其运算.专题:集合.分析:根据补集的定义进行计算即可.解答:解: 集合U={1,2,3,4,5,6,7},M={2,4,7},∴CUM={1,3,5,6},故选:C.点评:本题考查了补集的定义及其运算,是一道基础题.2.i为虚数单位,若=,则z等于()A.﹣3+4iB.3+4iC.﹣3﹣4iD.3﹣4i考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:利用复数代数形式的乘除运算化简,然后由共轭复数的概念得答案.解答:解: ==,∴z==﹣3﹣4i.故选:C.点评:本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.3.在下面给出的函数中,哪一个函数既是区间上的增函数又是以π为周期的偶函数?()A.y=x2(x∈R)B.y=|sinx|(x∈R)C.y=cos2x(x∈R)D.y=esin2x(x∈R)考点:三角函数的周期性及其求法.专题:压轴题.分析:根据函数的周期性和三角函数的单调性对选项逐一验证即可.解答:解:y=x2(x∈R)不是周期函数,故排除A.y=|sinx|(x∈R)周期为π,且根据正弦图象知在区间上是增函数,故B成立.y=cos2x(x∈R)是区间上的减函数,故排除C;y=esin2x(x∈R)在区间上是先增后减函数,故排除D.1故选:B.点评:本题主要考查三角函数的最小正周期和三角函数的图象.4.若实数m满足0<m<8,则曲线C1:﹣=1与曲线C2:﹣=1的()A.焦距相等B.实半轴长相等C.虚半轴长相等D.离心率相等考点:双曲线的标准方程.专题:圆锥曲线的定义、性质与方程.分析:根据m的取值范围,判断曲线为对应的双曲线,以及a,b,c的大小关系即可得到结论.解答:解:当0<m<8,则0<8﹣m<8,16<24﹣m<24,即曲线C1:﹣=1表示焦点在x轴上的双曲线,其中a2=24,b2=8﹣m,c2=32﹣m,曲线C2:﹣=1表示焦点在x轴上的双曲线,其中a′2=24﹣m,b′2=8,c′2=32﹣m,即两个双曲线的焦距相等,故选:A.点评:本题主要考查双曲线的方程和性质,根据不等式的范围判断a,b,c是解决本题的关键.5.已知命题p:若a,b是任意实数,且a>b,则a2>b2,命题q:若a,b是任意实数,且a>b,则()a<()b.在命题①p∧q;②p∨q;③p∧(¬q);④(¬p)∨q中,真命题的个数是()A.1个B.2个C.3个D.4个考点:复合命题的真假.专题:简易逻辑.分析:先判断出p,q的真假,再判断出复合命题的真假,从而得到答案.解答:解:已知命题p:若a,b是任意实数,且a>b,则a2>b2不一定成立,∴命题p是假命题,命题q:若a,b是任意实数,且a>b,则()a<()b,∴命题q是真命题,∴p∧q是假命题,p∨q是真命题,p∧(¬q)是假命题,(¬p)∨q是真命题,故选:B.2点评:本题考查了复合命题的判断问题,考查指数函数的单调性,本题属于基础题.6.设变量x,y满足约束条件,则目标函数z=3x﹣y的取值范围是()A.B.C.[﹣1,6]D.考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式组表示的平面区域;作出目标函数对应的直线;由目标函数中z的几何意义可求z的最大值与最小值,进而可求z的范围解答:解:作出不等式组表示的平面区域,如图所示由z=3x﹣y可得y=3x﹣z,则﹣z为直线y=3x﹣z在y轴上的截距,截距越大,z越小结合图形可知,当直线y=3x﹣z平移到B时,z最小,平移到C时z最大由可得B(,3),由可得C(2,0),zmax=6∴故选A点评:本题考查画不等式组表示的平面区域、考查数形结合求函数的最值.解题的关键是准确理解目标函数的几何意义7.设sin(+θ)=,则sin2θ=()3A.﹣B.﹣C.D.考点:二倍角的正弦.专题:三角函数的求值.分析:将已知由两角和的正弦公式展开可得(sinθ+cosθ)=,两边平方可得(1+sin2θ)=,即可得解.解答:解: sin(+θ)=,∴(sinθ+cosθ)=,∴两边平方,可得:(1+sin2θ)=,解得:sin2θ=﹣,故选:B.点评:本题主要考查了二倍角的正弦公式及两角和的正弦公...