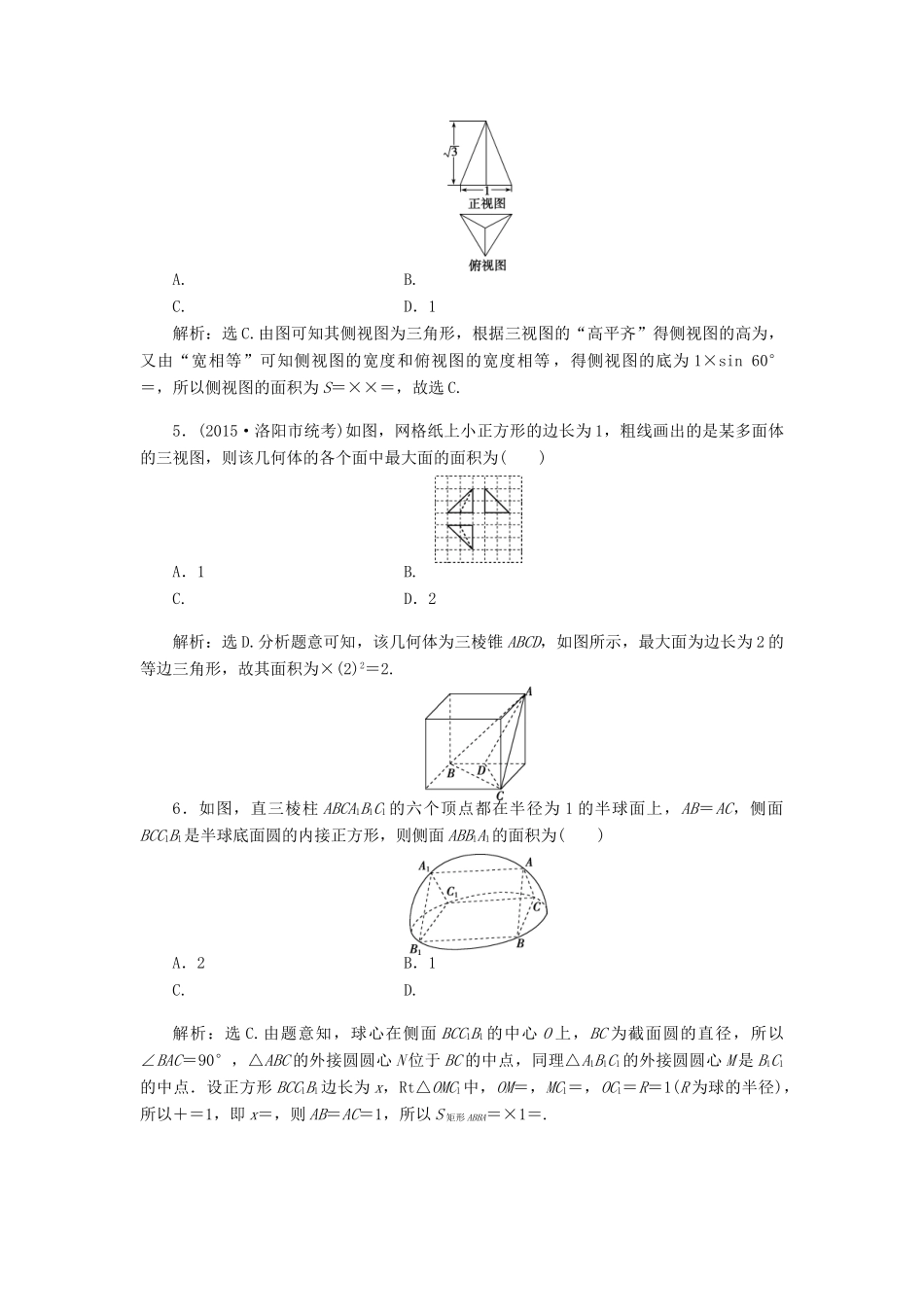
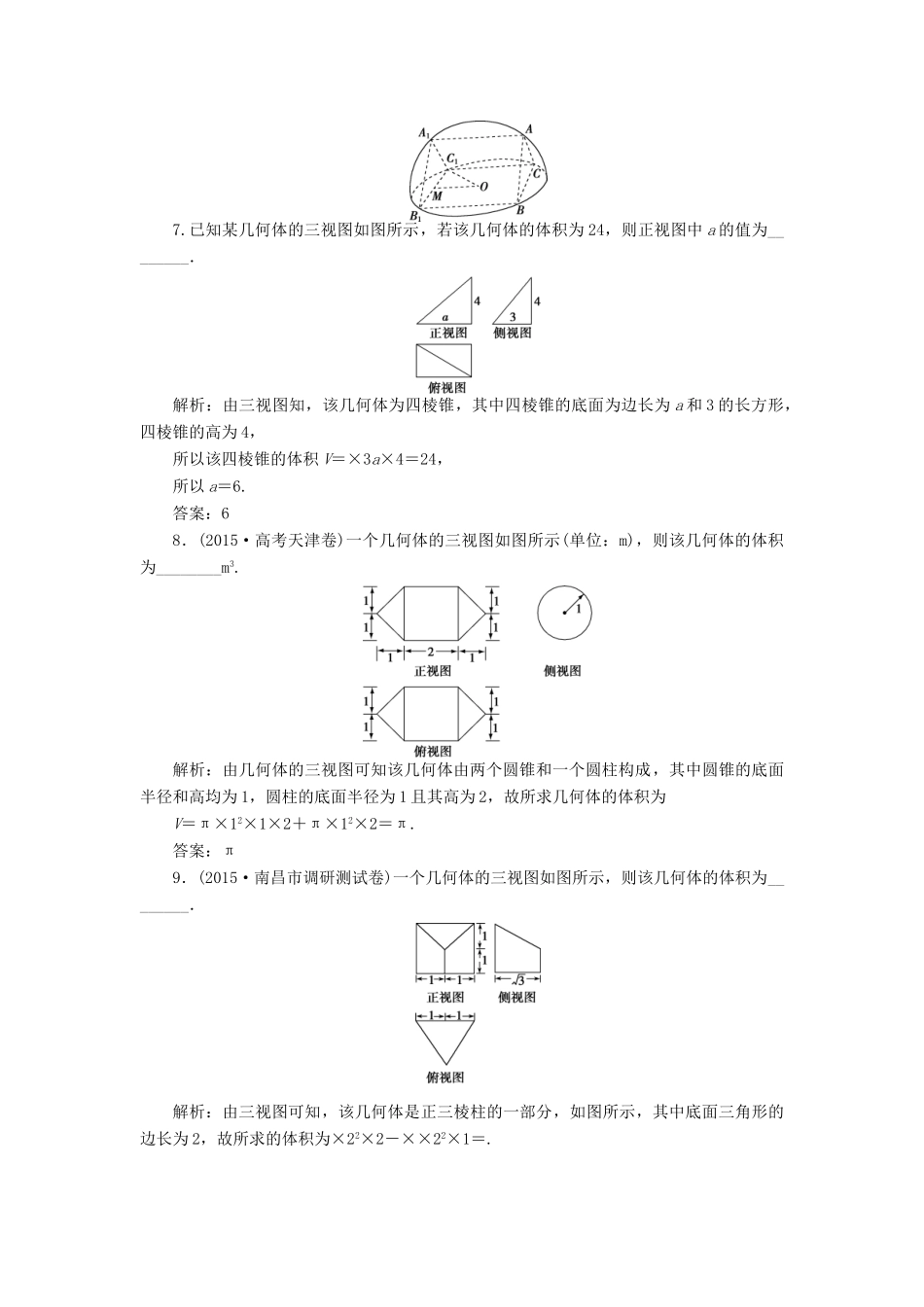
【优化方案】(山东专用)2016年高考数学二轮复习高考热点追踪(四)专题强化精练提能理1.(2015·高考广东卷)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是()A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交解析:选D.由直线l1和l2是异面直线可知l1与l2不平行,故l1,l2中至少有一条与l相交.2.某几何体的三视图如图所示,则该几何体外接球的表面积为()A.B.C.4πD.16π解析:选D.如图所示,由三视图可知该几何体为圆锥,AD为该圆锥外接球的直径,则AO=1,CO=,由射影定理可知CO2=AO·OD,得OD=3,所以外接球的半径为(AO+OD)=2,表面积为4π×22=16π.3.设a,b,c是三条不同的直线,α,β是两个不同的平面,则a⊥b的一个充分条件为()A.a⊥c,b⊥cB.α⊥β,a⊂α,b⊂βC.a⊥α,b∥αD.a⊥α,b⊥α解析:选C.A中,若a⊥c,b⊥c,则直线a与直线b可能异面,可能平行,可能垂直,所以此选项错误;B中,若α⊥β,a⊂α,b⊂β,则直线a与直线b可能异面,可能平行,可能垂直,所以此选项错误;C中,若a⊥α,b∥α,则根据线与线的位置关系可得a⊥b,所以C正确;D中,若a⊥α,b⊥α,则根据线面垂直的性质定理可得a∥b.故选C.4.已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为()A.B.C.D.1解析:选C.由图可知其侧视图为三角形,根据三视图的“高平齐”得侧视图的高为,又由“宽相等”可知侧视图的宽度和俯视图的宽度相等,得侧视图的底为1×sin60°=,所以侧视图的面积为S=××=,故选C.5.(2015·洛阳市统考)如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为()A.1B.C.D.2解析:选D.分析题意可知,该几何体为三棱锥ABCD,如图所示,最大面为边长为2的等边三角形,故其面积为×(2)2=2.6.如图,直三棱柱ABCA1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为()A.2B.1C.D.解析:选C.由题意知,球心在侧面BCC1B1的中心O上,BC为截面圆的直径,所以∠BAC=90°,△ABC的外接圆圆心N位于BC的中点,同理△A1B1C1的外接圆圆心M是B1C1的中点.设正方形BCC1B1边长为x,Rt△OMC1中,OM=,MC1=,OC1=R=1(R为球的半径),所以+=1,即x=,则AB=AC=1,所以S矩形ABBA=×1=.7.已知某几何体的三视图如图所示,若该几何体的体积为24,则正视图中a的值为________.解析:由三视图知,该几何体为四棱锥,其中四棱锥的底面为边长为a和3的长方形,四棱锥的高为4,所以该四棱锥的体积V=×3a×4=24,所以a=6.答案:68.(2015·高考天津卷)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.解析:由几何体的三视图可知该几何体由两个圆锥和一个圆柱构成,其中圆锥的底面半径和高均为1,圆柱的底面半径为1且其高为2,故所求几何体的体积为V=π×12×1×2+π×12×2=π.答案:π9.(2015·南昌市调研测试卷)一个几何体的三视图如图所示,则该几何体的体积为________.解析:由三视图可知,该几何体是正三棱柱的一部分,如图所示,其中底面三角形的边长为2,故所求的体积为×22×2-××22×1=.答案:10.(2015·日照二模)如图,在边长为2的正方形ABCD中,点E、F分别是边AB、BC的中点,△AED、△EBF、△FCD分别沿DE、EF、FD折起,使A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为________.解析:由题意知DF=,A′E=A′F=1,A′D=2,以A′E、A′F、A′D为棱,建立一个长方体,则体对角线长为2R=(R为球的半径),R=.答案:11.(2015·高考重庆卷)如图,三棱锥PABC中,PC⊥平面ABC,PC=3,∠ACB=.D,E分别为线段AB,BC上的点,且CD=DE=,CE=2EB=2.(1)证明:DE⊥平面PCD;(2)求二面角APDC的余弦值.解:(1)证明:由PC⊥平面ABC,DE⊂平面ABC,得PC⊥DE.由CE=2,CD=DE=,得△CDE为等腰直角三角形,故CD⊥DE.由PC∩CD=C,DE垂直于平面PCD...