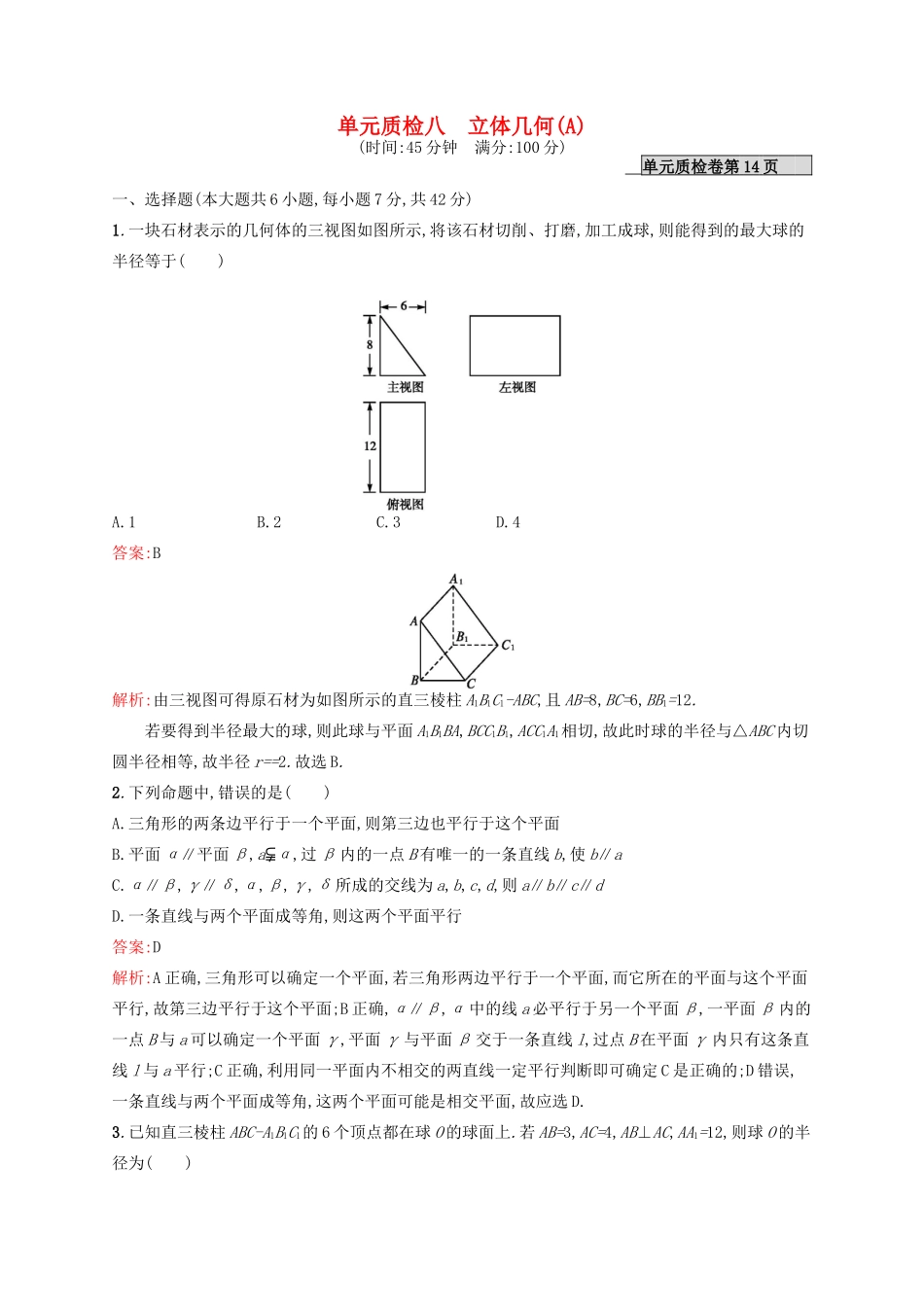
单元质检八立体几何(A)(时间:45分钟满分:100分)单元质检卷第14页一、选择题(本大题共6小题,每小题7分,共42分)1.一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4答案:B解析:由三视图可得原石材为如图所示的直三棱柱A1B1C1-ABC,且AB=8,BC=6,BB1=12.若要得到半径最大的球,则此球与平面A1B1BA,BCC1B1,ACC1A1相切,故此时球的半径与△ABC内切圆半径相等,故半径r==2.故选B.2.下列命题中,错误的是()A.三角形的两条边平行于一个平面,则第三边也平行于这个平面B.平面α∥平面β,a⫋α,过β内的一点B有唯一的一条直线b,使b∥aC.α∥β,γ∥δ,α,β,γ,δ所成的交线为a,b,c,d,则a∥b∥c∥dD.一条直线与两个平面成等角,则这两个平面平行答案:D解析:A正确,三角形可以确定一个平面,若三角形两边平行于一个平面,而它所在的平面与这个平面平行,故第三边平行于这个平面;B正确,α∥β,α中的线a必平行于另一个平面β,一平面β内的一点B与a可以确定一个平面γ,平面γ与平面β交于一条直线l,过点B在平面γ内只有这条直线l与a平行;C正确,利用同一平面内不相交的两直线一定平行判断即可确定C是正确的;D错误,一条直线与两个平面成等角,这两个平面可能是相交平面,故应选D.3.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为()A.B.2C.D.3导学号〚32470624〛答案:C解析:由计算可得O为B1C与BC1的交点.设BC的中点为M,连接OM,AM,则可知OM⊥面ABC,连接AO,则AO的长为球半径,可知OM=6,AM=,在Rt△AOM中,由勾股定理得R=.4.设α,β,γ是三个不重合的平面,l是直线,给出下列四个命题:①若α⊥β,l⊥β,则l∥α;②若l⊥α,l∥β,则α⊥β;③若l上有两点到α的距离相等,则l∥α;④若α⊥β,α∥γ,则γ⊥β.其中正确命题的序号是()A.①②B.①④C.②④D.③④答案:C解析:①若α⊥β,l⊥β,则l∥α或l⫋α,故①不正确;②l∥β,则过l作一平面γ使平面β与γ相交,交线设为l',那么l∥l'. l⊥α,∴l'⊥α.又l'⫋β,∴α⊥β,故②正确;③不正确,如l与平面α相交;④正确.5.(2016河北衡水中学高三(上)四调改编)某几何体的三视图如图所示,则该几何体的体积为()A.4B.C.D.答案:B解析:根据几何体的三视图,可知该几何体是四棱锥M-PSQN,如图,把该四棱锥放入棱长为2的正方体中,所以该四棱锥的体积VM-PSQN=V三棱柱QSD-NPM-V三棱锥S-DMQ=×22×2-×22×2=.6.在空间四边形ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC的形状是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定答案:B解析:作AE⊥BD,交BD于E, 平面ABD⊥平面BCD,∴AE⊥平面BCD,BC⫋平面BCD,∴AE⊥BC,而DA⊥平面ABC,BC⫋平面ABC,∴DA⊥BC,又 AE∩AD=A,∴BC⊥平面ABD,而AB⫋平面ABD,∴BC⊥AB,即△ABC为直角三角形.故选B.二、填空题(本大题共2小题,每小题7分,共14分)7.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2.若它们的侧面积相等,且,则的值是.导学号〚32470625〛答案:解析:设两个圆柱的底面半径和高分别为r1,r2和h1,h2,由,得,则.由圆柱的侧面积相等,得2πr1h1=2πr2h2,即r1h1=r2h2,所以.8.已知PA垂直于平行四边形ABCD所在的平面,若PC⊥BD,则平行四边形ABCD的形状一定是.导学号〚32470626〛答案:菱形解析:由于PA⊥平面ABCD,BD⫋平面ABCD,所以PA⊥BD.又PC⊥BD,且PC⫋平面PAC,PA⫋平面PAC,PC∩PA=P,所以BD⊥平面PAC.又AC⫋平面PAC,所以BD⊥AC.又四边形ABCD是平行四边形,所以四边形ABCD是菱形.三、解答题(本大题共3小题,共44分)9.(14分)如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在右面画出(单位:cm).(1)在主视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连接BC',证明BC'∥平面EFG.(1)解:如图:(2)解:所求多面体体积V=V长方体-V正三棱锥=4×4×6-×2=(cm3).(3)证明:在长方体ABCD-A'B'C'D'中,连接AD',则AD'∥BC'.因为E,G分别为AA',A'D'的中点,所以AD'∥EG,从而EG∥BC'.又BC'⊈平面EFG,所以BC'∥平面EFG.10.(15分)如图所示,在平行四边形ABCD中,∠DAB=60°,AB...