8函数y=Asin(ωx+φ)的图像与性质VIP免费

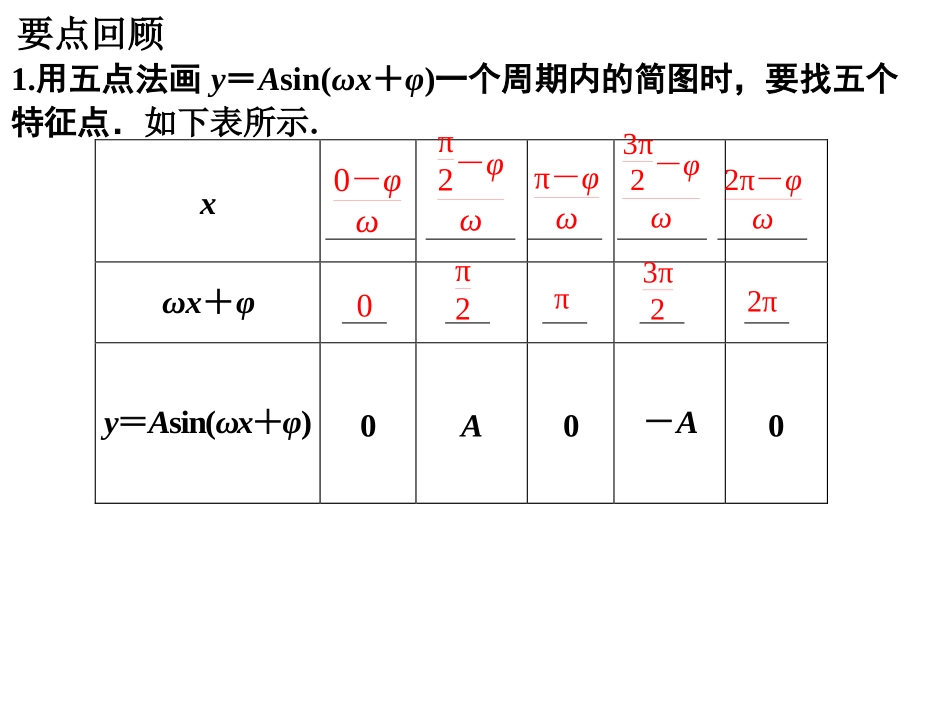
函数y＝Asin(ωx＋φ)的图象与性质学习目标：1、会用“五点法”画函数y＝Asin(ωx＋φ)的简图，理解A、ω、φ的物理意义；2、能灵活应用函数y＝Asin(ωx＋φ)（或y＝Acos(ωx＋φ)）的图象及其简单性质解决与之相关的一些实际问题；3、掌握三角函数的图象的平移变换、对称变换和伸缩变换。要点回顾1.用五点法画y＝Asin(ωx＋φ)一个周期内的简图时，要找五个特征点．如下表所示.xωx＋φy＝Asin(ωx＋φ)0A0－A00－φωπ2－φωπ－φω3π2－φω2π－φω0π2π3π22πk2k2kk3.函数y＝sinx的图象经变换得到y＝Asin(ωx＋φ)的图象的步骤如下：方法一画出y＝sinx的图象步骤1⇓得到y＝sinx＋φ的图象步骤2⇓得到y＝sinωx＋φ的图象步骤3⇓得到y＝Asinωx＋φ的图象步骤4向左(右)平移|φ|个单位长度各点的纵坐标变为原来的A倍各点的横坐标变为原来的1ω倍方法二画出y＝sinx的图象得到y＝sinωx的图象得到y＝sinωx＋φ的图象得到y＝Asinωx＋φ的图象各点的纵坐标变为原来的A倍各点的横坐标变为原来的1ω倍向左(右)平移φω个单位长度以上两种方法的区别：方法一先平移再伸缩；方法二先伸缩再平移．特别注意方法二中的平移量．基础自测1.(1)把y＝sin(x－π3)的图像上所有点的横坐标缩短到原来的12倍(纵坐标不变)得_____________的图像．(2)把y＝sin2x的图像向右平移π6得_____________的图像．y＝sin(2x－π3)y＝sin(2x－π3)2．若把函数y＝f(x)的图像沿x轴向左平移π4个单位，沿y轴向下平移1个单位，然后再把图像上每个点的横坐标伸长到原来的2倍(纵坐标保持不变)，得到函数y＝sinx的图像，则y＝f(x)的解析式为()A．y＝sin(2x－π4)＋1B．y＝sin(2x－π2)＋1C．y＝sin(12x＋π4)－1D．y＝sin(12x＋π2)－1B3．若x∈[－π，π]，则y＝sinx和y＝tanx的图像的交点个数是()A．2B．3C．4D．5B4.函数f(x)＝Asin(ωx＋φ)(其中A>0，ω>0，|φ|<π2)的图像如图所示，为了得到g(x)＝sin3x的图像，则只要将f(x)的图像()A．向右平移π4个单位长度B．向右平移π12个单位长度C．向左平移π4个单位长度D．向左平移π12个单位长度B5．将函数y＝sinx＋π3的图象向右平移π6个单位，再向上平移2个单位所得图象对应的函数解析式是______________y＝sinx＋π6＋2探究展示的图象不相切。与函数证明直线的单调递增区间；求函数；求对称轴是直线图象的一条）设函数)(025)3()()2()1.(8)(),0-(sin()(.1xfycyxxfxxfyxxf43)(85,8Zkkk2)432cos(2/xy的值。和是单调函数，求，对称且在区间关于点上的偶函数，其图像是已知函数2,0)0,43()0,0)(sin()(.2MRxxf232,2或3.求下列函数的值域；(1)y＝sin2xsinx1－cosx；(2)y＝sinx＋cosx＋sinxcosx；[－12，4)[－1，2＋12](3)f(x)＝2－sinx2＋cosx(4)f(x)＝12(sinx＋cosx)－12|sinx－cosx|。[4－73，4＋73]－1≤y≤22(1)y＝2cosx1－cos2x1－cosx＝2cos2x＋2cosx＝2(cosx＋12)2－12.于是当且仅当cosx＝1时，ymax＝4，但cosx≠1，∴y<4.且ymin＝－12，当且仅当cosx＝－12时取得．故函数值域为[－12，4)．(2)令t＝sinx＋cosx则sinxcosx＝t2－12.y＝f(t)＝t＋t2－12＝12(t＋1)2－1(－2≤t≤2)故y＝f(t)＝12(t＋1)2－1(－2≤t≤2)，从而知：f(－1)≤y≤f(2)，即－1≤y≤2＋12.(3)函数f(x)＝2－sinx2＋cosx，可看作点(2,2)，(－cosx，sinx)两点连线的斜率．点(－cosx，sinx)的轨迹为x2＋y2＝1.切线方程为y－2＝k(x－2)即kx－y－2k＋2＝0(4)f(x)＝sinxsinx≤cosxcosxsinx>cosx－1≤y≤22满足|2－2k|1＋k2＝1，解之得k＝4±73例1、已知函数y＝2sin2x＋π3，(1)求它的振幅、周期、初相；(2)用“五点法”作出它在一个周期内的图象；(3)说明y＝2sin2x＋π3的图象可由y＝sinx的图象经过怎样的变换而得到．例2、(1)(2011·江苏)已知f(x)＝Asin(ωx＋φ)(A，ω，φ为常数，A>0，ω>0)的部分图象如图所示，则f(...