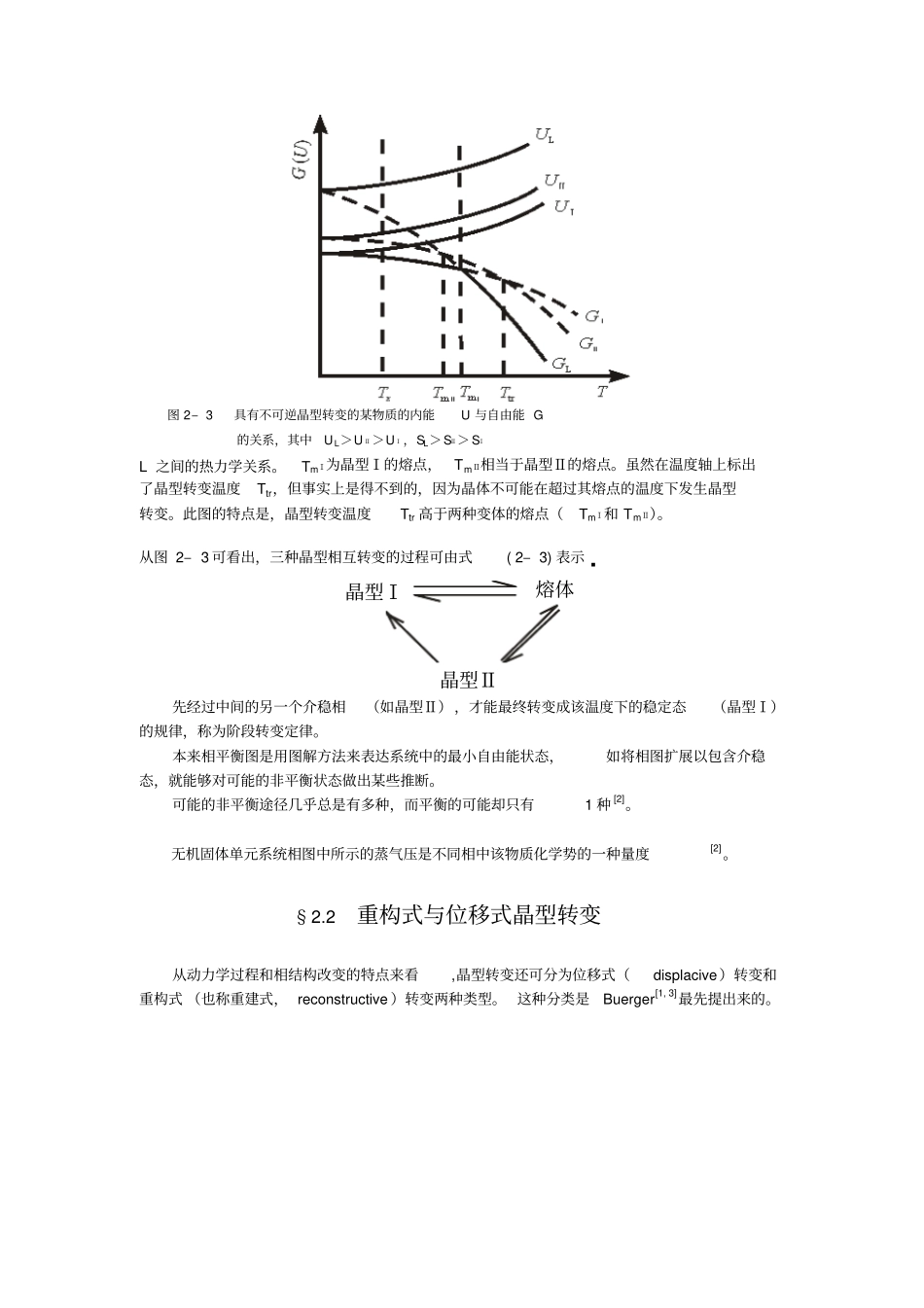
第二章晶型转变及其控制方法系统中存在的相,可以是稳定、介稳或不稳定的。其吉布斯自由能如图2–1所示。当系统的温度、压力或对系统的平衡发生影响的电场、磁场等条件发生改变时,这种介稳或不稳定状态下的自由能会发生改变,相的结构(原子或电子分布)也相应地发生变化。此外,在一定的条件下,一种稳定相也可以转变成另一种稳定相,此即下文所说的可逆晶型转变。对某一特定系统而言,相的自由能改变所伴随的结构改变过程,叫做相转变或相变。图2–1稳定态、介稳态和不稳定态化学组成相同的固体,在不同的热力学条件下,常会形成晶体结构不同的同质异构体(polymorph)[1,2]或称为变体(modification),这种现象叫同质多晶或同质多相(polymorphism)[2]现象。当温度和压力条件变化时,变体之间会发生相互转变,此称为晶型转变。显然,晶型转变是相变的一种,也是最常见的一种固–固相变形式。由于晶型转变,晶体材料的力学、电学、磁学等性能会发生巨大的变化。例如,碳由石墨结构转变为金刚石结构后硬度超强,BaTiO3由立方结构转变为四方结构后具有铁电性。可见,通过相变改变结构可达到控制固体材料性质的目的。相律的表达式是自由度f=C–Φ+2,C为独立组元(组分)数,Φ为相数,数字2代表温度和压力2个变量。对于凝聚系统来说,压力的影响可以忽略不计,于是温度成了惟一的外界条件。在这种情况下,相律可写成f*=C–Φ+1,f*被称为条件自由度。对于单元(单组分)系统来说,C=1,f*=2–Φ。由于所讨论的系统至少有1个相,所以单元凝聚系统条件自由度数最多等于1,系统的状态仅仅由温度1个独立变量所决定。于是,在许多情况下,单元系统相变往往用流程图来表示,例如本章§2.3节对BaTiO3晶型转变所采用的表示法。在另一些场合下,考虑压力变量的影响对讨论问题是有利的。由于凝聚系统的平衡蒸气压实际上仍比大气压低得多,所以在讨论单元凝聚系统相图时,往往把压力坐标(纵标)加以夸大,画出来的相图中的曲线仅仅表示温度变化时系统中压力变化的大致趋势,这种情况如在本章§2.4~§2.6中所描述的SiO2、ZrO2和Ca2SiO4(C2S)单元系统带有晶型转变的相图。本章在大部分场合下假定读者已具备了足够的物理化学和结晶化学的知识。§2.1可逆与不可逆晶型转变对于一个单元系统,各种变体的吉布斯自由能GG=U+pV–TS,(2–1)式中U为该变体的内能;p是平衡蒸气压,对于凝聚体系,p-般很小;V是体积,晶型转变时,体积变化一般不大;pV项常可忽略不计[2];T是绝对温度;S是一定晶型的熵。绝对零度时,吉布斯自由能G基本由内能项决定[2]。晶型转变有可逆转变与不可逆转变之分。图2-2图2-2具有可逆晶型转变的某物质内能U与自由能G的关系[2],其中UL>UⅡ>UⅠ,SL>SⅡ>SⅠ逆晶型转变的不同变体晶型Ⅰ和晶型Ⅱ以及其液相L之间的热力学关系。对上述物质进行加热或冷却时,发生了如下的晶型转变:晶型Ⅰ晶型Ⅱ液相。(2–2)当晶型Ⅰ过热(超过Ttr)而介稳存在时,其自由能GⅠ的变化以虚线表示,同时,当液相过冷(低于TmⅡ)处于介稳态时,其自由能GL曲线也以虚线表示;与GL和GⅠ有关的两虚线交于TmⅠ,TmⅠ相当于晶型Ⅰ的熔点。图2–2的特点是晶型转变温度Ttr低于两种变体的熔点(TmⅠ和TmⅡ)。也有一些晶体的变体之间不可能发生可逆晶型转变。图2–3表示具有不可逆晶型转变的不同变体晶型Ⅰ、晶型Ⅱ及它们的液相图2–3具有不可逆晶型转变的某物质的内能U与自由能G的关系,其中UL>UⅡ>UⅠ,SL>SⅡ>SⅠL之间的热力学关系。TmⅠ为晶型Ⅰ的熔点,TmⅡ相当于晶型Ⅱ的熔点。虽然在温度轴上标出了晶型转变温度Ttr,但事实上是得不到的,因为晶体不可能在超过其熔点的温度下发生晶型转变。此图的特点是,晶型转变温度Ttr高于两种变体的熔点(TmⅠ和TmⅡ)。从图2–3可看出,三种晶型相互转变的过程可由式(2–3)表示.晶型Ⅰ熔体晶型Ⅱ先经过中间的另一个介稳相(如晶型Ⅱ),才能最终转变成该温度下的稳定态(晶型Ⅰ)的规律,称为阶段转变定律。本来相平衡图是用图解方法来表达系统中的最小自由能状态,如将相图扩展以包含介稳态,就能够对可能的非平衡状态做出某些推断。可能的非平衡途径几乎总是...