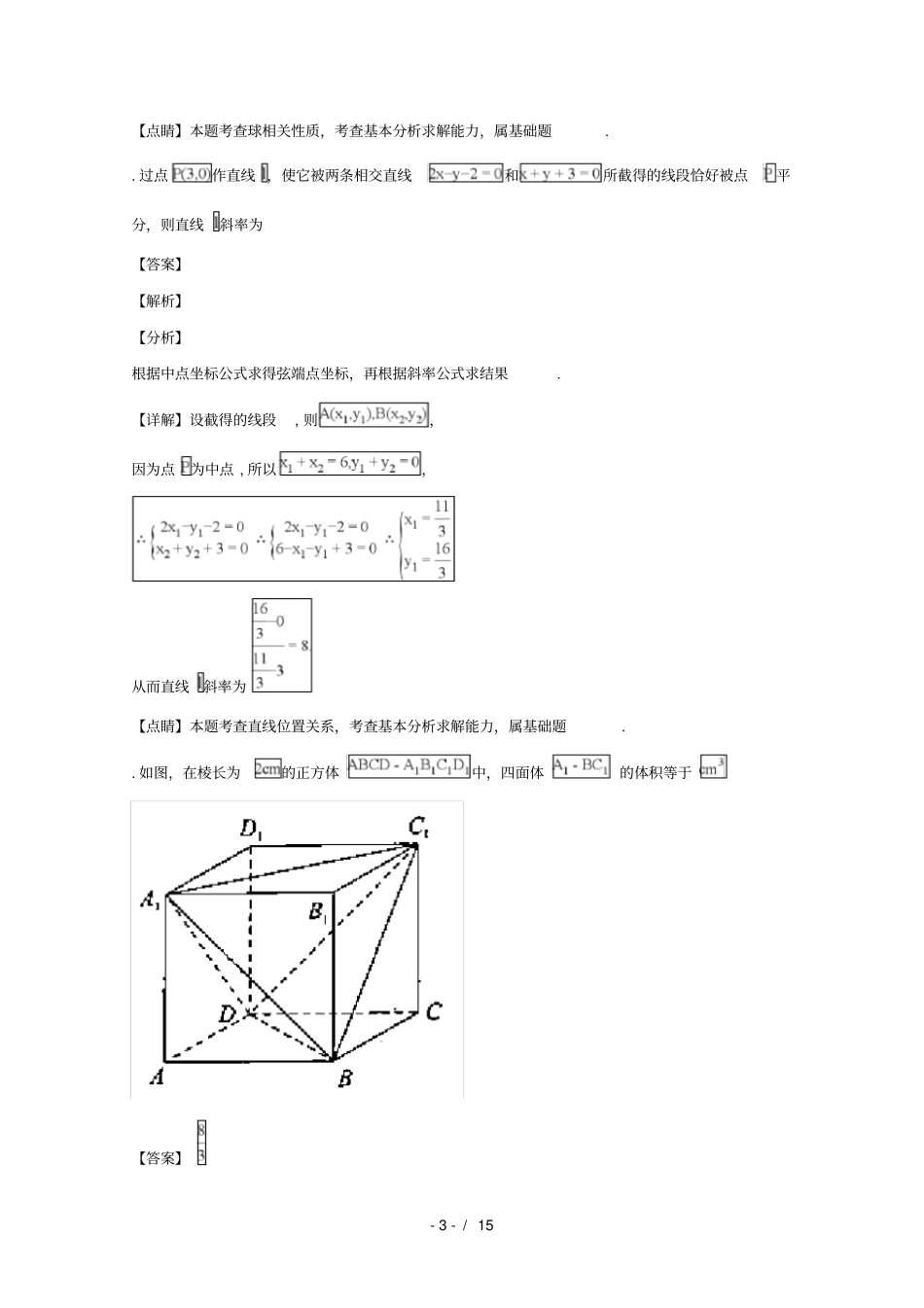
-1-/15江苏省昆山市学年高二数学上学期期中试题(含解析)一、填空题.已知倾斜角为°的直线经过点(),(,-),则的值为.【答案】【解析】【分析】根据直线倾斜角的定义可得,解出即可.【详解】∵倾斜角为°的直线经过点,,∴,解得,故答案为.【点睛】本题考查了倾斜角的应用,考查了基本概念,属于基础题..已知直线和直线平行,则的值为【答案】【解析】【分析】根据直线平行的等量关系,解得结果.【详解】由题意得,所以,(舍).【点睛】本题考查直线平行,考查基本分析求解能力,属基础题..若长方体的三个面的对角线分别为,则长方体的对角线长度为【答案】【解析】【详解】设长方体长宽高为,则,所以,即对角线长为.【点睛】本题考查长方体对角线长,考查基本分析求解能力,属基础题..直线被圆截得的弦长等于-2-/15【答案】【解析】【分析】根据垂径定理求弦长.【详解】因为,所以,因此圆心到直线距离为,弦长为【点睛】本题考查直线与圆位置关系,考查基本分析求解能力,属基础题..圆心在直线上,且与直线相切于点的圆的标准方程为【答案】【解析】【分析】设圆标准方程形式,根据条件列方程组,解得结果.【详解】设,则,解得,所以圆的标准方程为.【点睛】本题考查圆得标准方程,考查基本分析求解能力,属基础题..半径为的球被两个相互平行的平面截得的圆的半径分别为和,则这两个平面之间的距离是【答案】或【解析】【分析】先根据条件得球心到两平面距离,再根据两平面位置关系得结果.【详解】由题意得球心到两平面距离分别为,因此这两个平面之间的距离是或-3-/15【点睛】本题考查球相关性质,考查基本分析求解能力,属基础题..过点作直线,使它被两条相交直线和所截得的线段恰好被点平分,则直线斜率为【答案】【解析】【分析】根据中点坐标公式求得弦端点坐标,再根据斜率公式求结果.【详解】设截得的线段,则,因为点为中点,所以,从而直线斜率为【点睛】本题考查直线位置关系,考查基本分析求解能力,属基础题..如图,在棱长为的正方体中,四面体的体积等于【答案】-4-/15【解析】【分析】根据割补法得结果.【详解】四面体的体积等于正方体体积减去四个小三棱锥体积,即.【点睛】本题考查锥体体积,考查基本分析求解能力,属基础题..如图,空间四边形中,平面,为的等边三角形,,,为棱上的一个动点,则的最小值为【答案】【解析】【分析】先展开,再在平面内利用余弦定理得结果.【详解】先将平面展开到平面,则的最小值为此时,.【点睛】本题考查利用展开图求距离最值,考查基本分析求解能力,属基础题..设,过定点的动直线和过定点的动直线交于点,则的最大值是【答案】-5-/15【解析】【分析】可得直线分别过定点(,)和(,)且垂直,可得.三角换元后,由三角函数的知识可得的最大值.【详解】由题意可得(,),由于直线﹣﹣,即(﹣)﹣,显然经过定点(,),注意到动直线和动直线﹣﹣始终垂直,又是两条直线的交点,则有⊥,∴.设∠θ,则θ,θ.∵≥且≥,可得θ∈[,],∴θθ[θθ)(θ),∵θ∈[,],∴θ∈[,],∴当θ时,(θ)取得最大值为,故答案为:.【点睛】本题考查直线过定点问题,涉及直线的垂直关系和三角恒等变换,正弦函数的定义域和值域,属中档题..关于异面直线,有下列四个命题①过直线有且只有一个平面,使得②过直线有且只有一个平面,使得③在空间存在平面,使得,④在空间不存在平面,使得,其中,一定正确的是【答案】①③④【解析】【分析】根据异面直线定义说明命题正确①③④,举反例说明命题②错误.【详解】①过直线上任一点作直线平行线,则直线必相交,即确定一个平面,因为若存在平面,使得,则,与为异面直线矛盾,