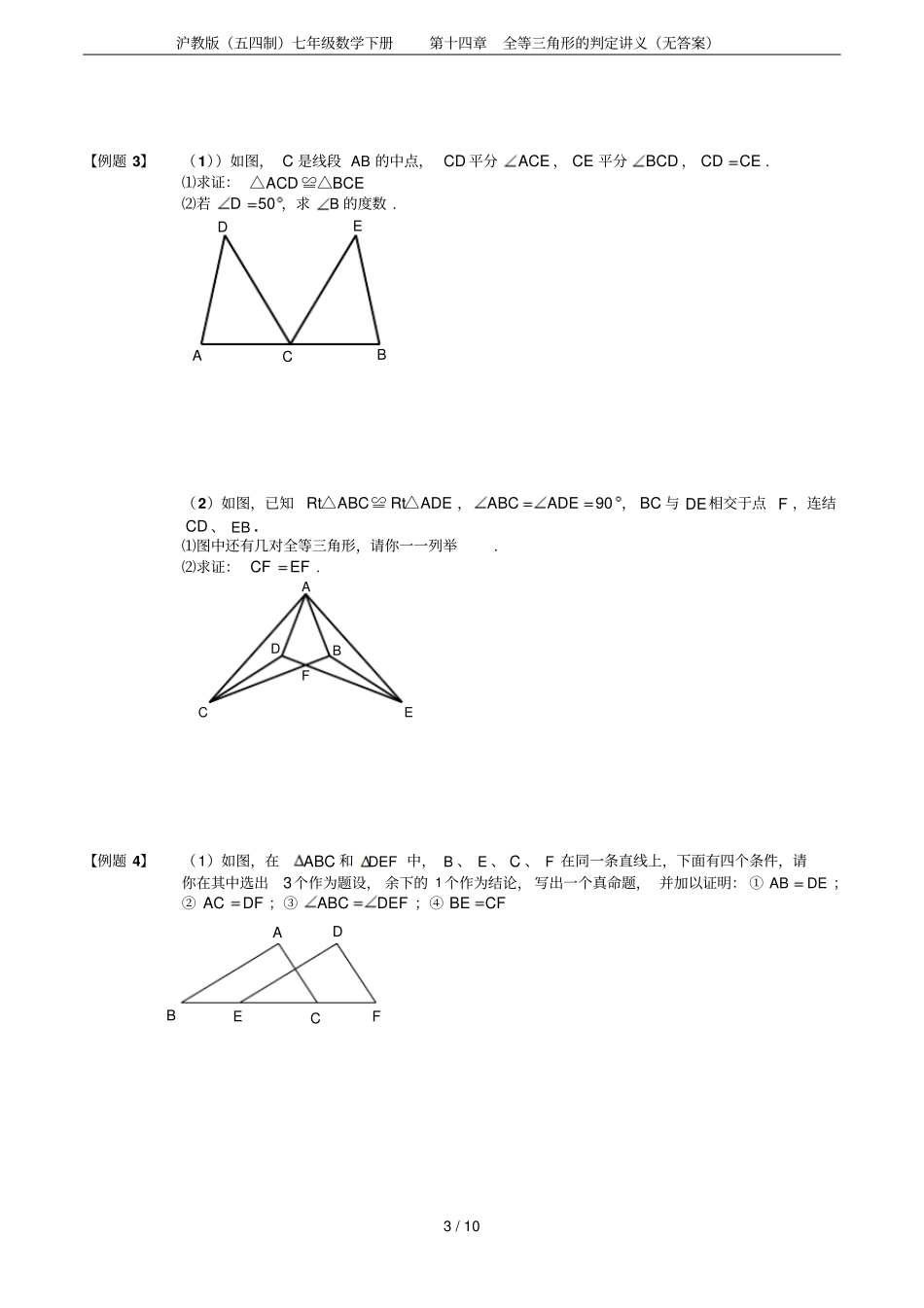
沪教版(五四制)七年级数学下册第十四章全等三角形的判定讲义(无答案)1/10第三讲全等三角形的判定一.全等三角形的定义与性质:1.全等三角形:能够完全重合的两个三角形叫全等三角形.2.两个全等三角形,经过运动后一定重合.①对应顶点:相互重合的顶点叫做对应顶点.②对应边:相互重合的边叫做对应边.③对应角:相互重合的角叫做对应角.如图,△ABC与△A’B’C’是全等三角形,记作“△ABC≌△A’B’C’,符号“≌”表示全等,读作“全等于”.其中顶点A、B、C分别与顶点A’、B’、C’是对应顶点.3.全等三角形的性质:①全等三角形的对应边相等.②全等三角形的对应角相等.二.全等三角形的判定:①有两边和它们的夹角对应相等的两个三角形全等(简称“SAS”)②有两角和它们的夹边对应相等的两个三角形全等(简称“ASA”)③有两角和其中一角的对边对应相等的两个三角形全等(简称“AAS”)④有三边对应相等的两个三角形全等(简称“SSS”)⑤有斜边和一条直角边对应相等的两个直角三角形全等(简称“HL”)三、全等三角形的证明格式:在△ABC和△A'B'C'中''()='''()ABABAAACAC理由(理由)理由△ABC≌△A'B'C'(S.A.S)''BCBC(全等三角形的对应边相等)'BB(全等三角形的对应角相等)沪教版(五四制)七年级数学下册第十四章全等三角形的判定讲义(无答案)2/10【例题1】(1)如图,根据SAS,如果已知ABAC,=,即可判定ABDACE≌△△.(2)如图所示,点C在线段BE上,ACCD,ACCD,90BE,2AB,1DE,则BE.EDCBADECBA(1)(2)(3)(漳州市中考题)如图3,已知:CEAD于E,BFAD于F,你能说明BDF和CDE全等吗?若能,请你说明理由.若不能,在不用增加辅助线的情况下,请添加其中一个适当的条件,这个条件是,来说明这两个三角形全等,并且出证明过程FEDCBA(尖子)【例题2】⑴如图,BD垂直平分线段AC,AEBC,垂足为E,交BD于P点,3PEcm,求P点到直线AB的距离.PEDCBA(2)如图,在等腰RtABC△中,90C,ACBC,AD平分BAC交BC于D,DEAB于D,若10ABcm,求BDE△的周长.EDCBA沪教版(五四制)七年级数学下册第十四章全等三角形的判定讲义(无答案)3/10【例题3】(1))如图,C是线段AB的中点,CD平分ACE,CE平分BCD,CDCE.⑴求证:ACDBCE△≌△⑵若50D,求B的度数.EDCBA(2)如图,已知RtABCRtADE△≌△,90ABCADE,BC与DE相交于点F,连结CD、EB.⑴图中还有几对全等三角形,请你一一列举.⑵求证:CFEF.DBFECA【例题4】(1)如图,在ABC和DEF中,B、E、C、F在同一条直线上,下面有四个条件,请你在其中选出3个作为题设,余下的1个作为结论,写出一个真命题,并加以证明:①ABDE;②ACDF;③ABCDEF;④BECFFEDCBA沪教版(五四制)七年级数学下册第十四章全等三角形的判定讲义(无答案)4/10(2)已知:如图,四边形ABCD是边长为a的正方形,O是其中心;四边形OEFG是边长为b的正方形,OE交BC于M,OG交CD于N.求四边形OMCN的面积.NMGFEODCBA【例题5】已知BD、CE是ABC△的高,点P在BD的延长线上,且BPAC;点Q在CE的延长线上,且CQAB。求证:APAQ且APAQ。QPEDCBA【例题6】(1)已知:如图,//ABDC,ABDC,AEAD,AFAB,AEAD,ABAF.求证:ACEF.FEDCBA沪教版(五四制)七年级数学下册第十四章全等三角形的判定讲义(无答案)5/10(2)已知:如图,//ABCD,2DB,设ADa,DCb,求线段AB的长.DCBA【例题7】已知:如图,ABC△中,45ABC,CDAB于D,BE平分ABC,且BEAC于E,与CD相交于点F.H是BC边的中点,连结DH与BE相交于点G.⑴求证:BFAC⑵求证:12CEBF⑶CE与BG大小关系如何?试证明你的结论.HGFEDCBA【例题8】如图,公园有一条“Z”字形道路ABCD,其中//ABCD,在,,EMF处各有一个小石凳,且BECF,M为BC的中点,请问三个小石凳是否在一条直线上?说出你推断的理由.MFEDCBA【例题9】下列4个命题:⑴有两边及其中一边上的高对应相等的两个三角形全等;沪教版(五四制)七年级数学下册第十四章全等三角形的判定讲义(无答案)6/10⑵有两边及第三边上的高对应相等的两个三角形全等;⑶三角形6个边、角元素中,有5个元素分别相等的两个三角形全等;⑷一边及其他两边上的高对应相等的两个三角形全等;上述命题是否正确...