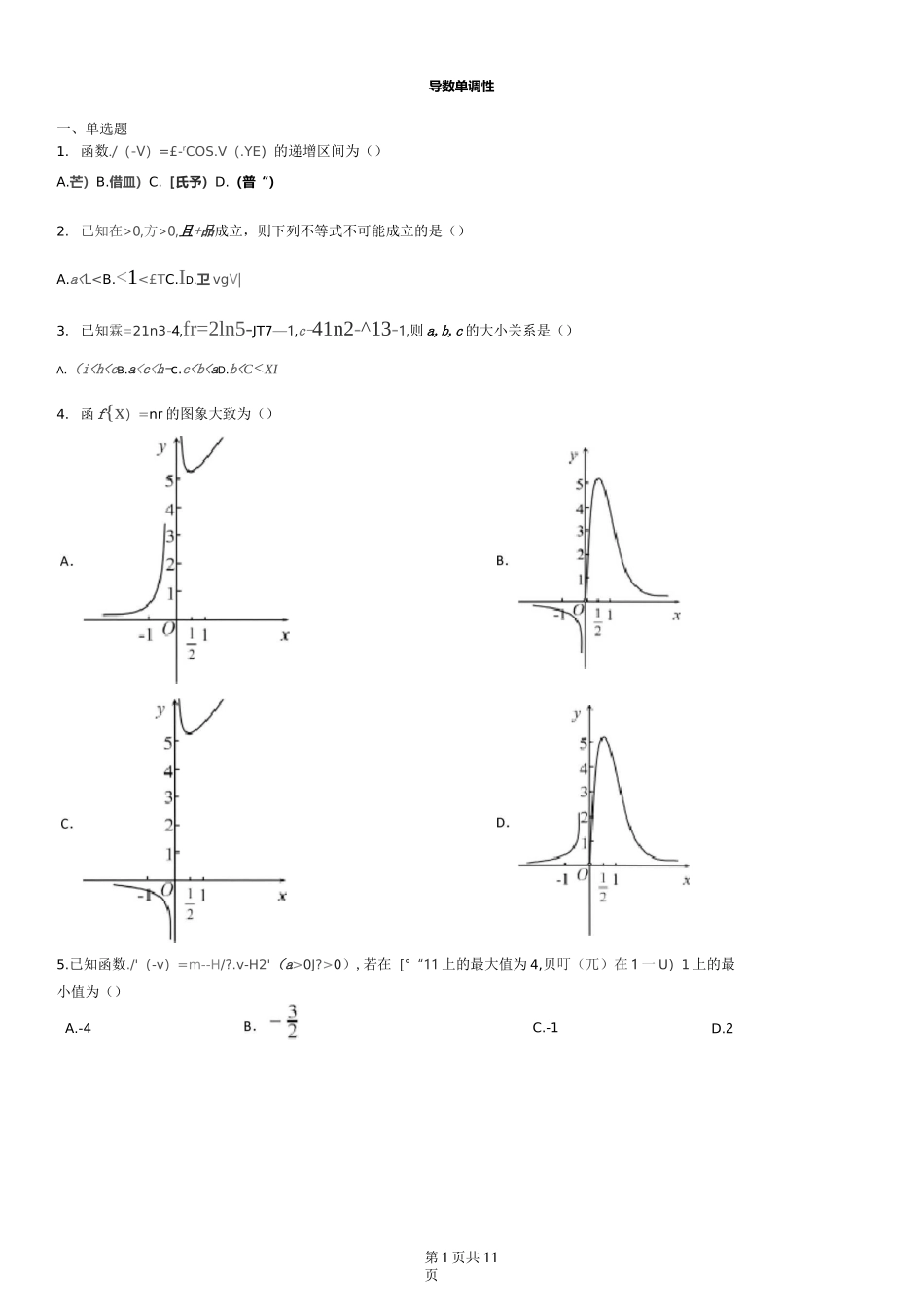
第1页共11页A.-4C.-1D.2导数单调性一、单选题1.函数./(-V)=£-rCOS.V(.YE)的递增区间为()A.芒)B.借皿)C.[氏予)D.(普“)2.已知在>0,方>0,且+品成立,则下列不等式不可能成立的是()A.a0J?>0),若在[°“11上的最大值为4,贝叮(兀)在1一U)1上的最小值为()第2页共11页:■■=_I.-1:,贝y:的最大值1的最小值是()D.7.已知各项均为正数的数列•::满足』一",;「」;:「一上:,其前n项和为、,则下列关于数列•:;的叙述错误的是()A.:i■■I:.;「一人:二、多选A2卫咗I..T,方程1/(-0\2-hifM=^ER)有两个不等实根,则下列选项正确的是()点是函数u的零点C■■二是的极大值点B.小,」,―丨,T,使'!,■:-'的取值范围是!丁一十9ABCD已知函数■'■■;JT―—―,贝y()■';;‘:是偶函数存在实数F使得,门衍)•‘;;’:在|,:上单调递增f(兀)存在极值点二、填空题10•已知定义在R上的函数心)的导函数FWI,且几2附i&f(用十I),则实数冋的取值范围为,11•函数s扫工+上心€[0_町)的最大值为四、解答题12•已知函数■';■:■::■:.(1)若;I,求::的单调区间;⑵若关于%的不等式"'1二恒成立,求实数a的取值范围.6•已知函数:::上-盘_壬_冊C.B.1第3页共11页13•己知函数'■■■:I-'■'⑴当I时,求:;;’:的单调区间.⑵存在;I,使得-■■■'I成立,求整数八的最小值.14•已知函数::・i厂,.‘.■-•(1)当•;I时,求":的单调区间;⑵若、w[lL号],不等式沏⑶呃)+玄冋二好⑴恒成立,求实数a的取值范围.15•求下列函数的单调区间(1)f(x)—~x2—lnx;(2^x)=x+—(b>0).第4页共11页16•用导数证明:⑴:::'1■■-在区间■':上是增函数;⑵在区间;’」;上是减函数.17.证明:⑴函数"丨在定义域上是减函数;18•确定下列函数的单调区间:(1)「--■;⑵'-'一■'第5页共11页19.设函数f(X)=A'lDA'+.⑴若迎=-1,求函数/(.V)的单调区间;⑵若函数f(V)有两个不同的零点,求实数门的取值范围.20.已知函数/(X)=(2-«)v-hx-I.⑴当压=1时,求曲线尸(X)在点(趴f(町)处的切线方程;(2)当^>0时,设£(工)=/(工)十如:丄,求函数g{工)的单调区间.21.试确定函数丫一*力一审一女+1的单调区间.22.已知函数/(A)=e'(w^--Y).(1)若⑷=2,求证:函数f(d)在只上单调递增;⑵若关于X的不等式十而冬酗亘成立,求实数加的最小值.23.已知函)-ln2丈0693,JI::丨64喑均为不足近似值.第6页共11页⑴当x>\时,判断函数f(尤)的单调性;⑵证明:当v>0时,不等式/(工)>予恒成立.24.已知函数/'(工)=』一0其中抚ER.⑴当a=2时,求函</(r)的单调区间;⑵当a-3时,函数fU有两个零点「,乜满足X.YU,证明,+衍>6.25.已知函</'(.¥)=ev-.⑴若讨论)的单调性;⑵若",比1是函数/(X)的两个不同的零点,证明:++第7页共11页26.己知函数/(工)=ln{1十姑)=\n\[+x]-十〒.⑴求r⑴的单调区间;(2)证明:gCU;電e■对任意的疋*都成立(其中亡是自然对数的底数).求口的最大值.27.己知函数/'(X)⑴若门=-1,求函数/■(.1-)的单调区间;(2)护E【(hL],求证:32/(x)>一丁.参考数据:bt3-L099fbi4~138628.己知函数/(-V)=^A-blA-F^,⑴若耐=-2,求函数<(.V)的单调区间;(2)若门绚且兀岸叼,证明:IHV|+HV2>2.第8页共11页29.己知函数/(戈)-vh.V的图象曲线C满足以下两个特性:①过点卩(I*’)存在两条直线与曲线C相切;②曲线c上有48两点,其横坐标分别为心,•巾{Q文可v兀2v1),且满足两点在曲线c上等高•请完成以下两个问题.⑴求实数t的取值范围;⑵若十甲J,且虫2,求広值.30.己知函数/'(X)—小+马曲+2^+扒其中砧⑴当d=—10时,求函数丿(丫}的单调性;⑵若对baE[-1J1,不等式『⑴O在[一1川上恒成立,求加勺取值范围.一电Bs叵'点叵凶増t+、母二逼—貳—展區凶SSLH=二詁—)5^85?—EW.蹩fflg*T(_「g—」出(二>二【CSrm?s®w^•了—“5黑叵凶雲二【W轴】7—」(迂g...