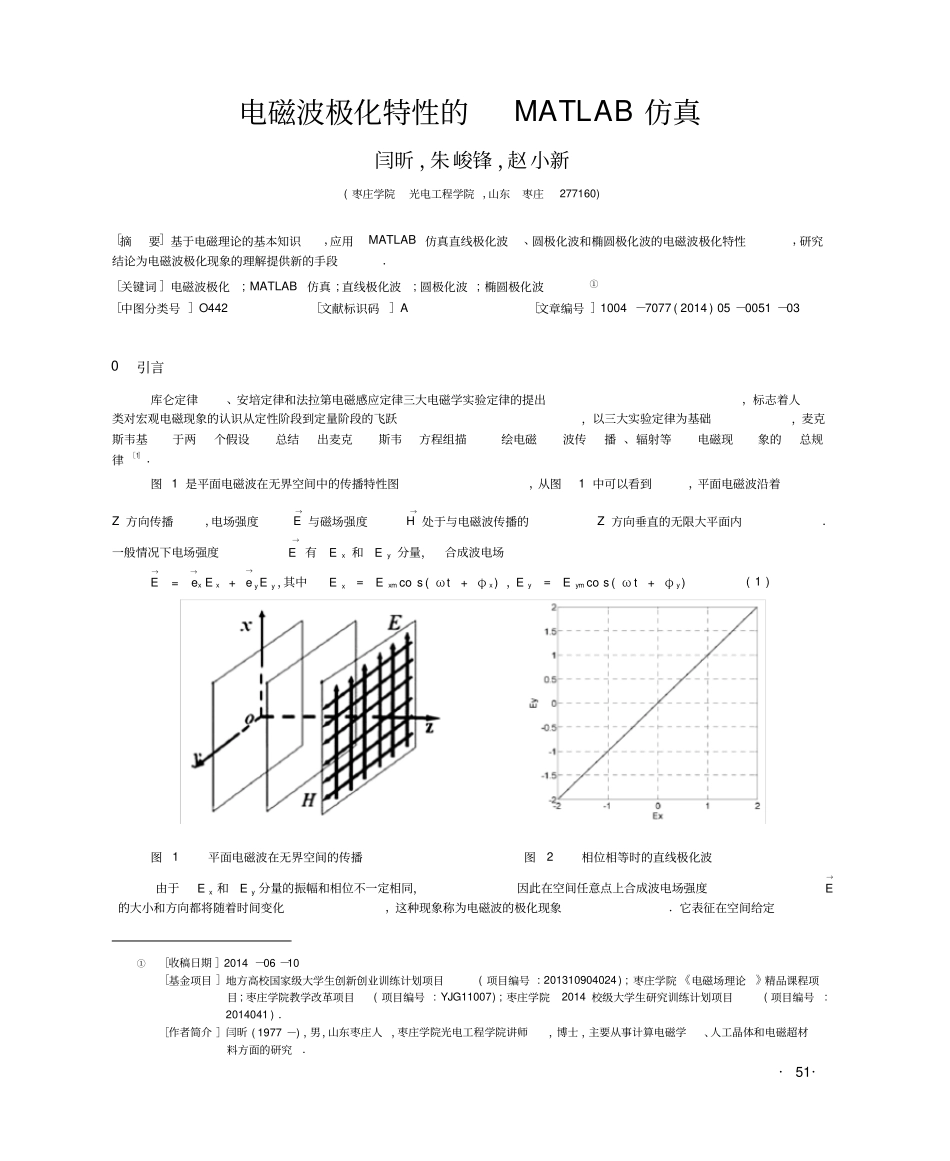
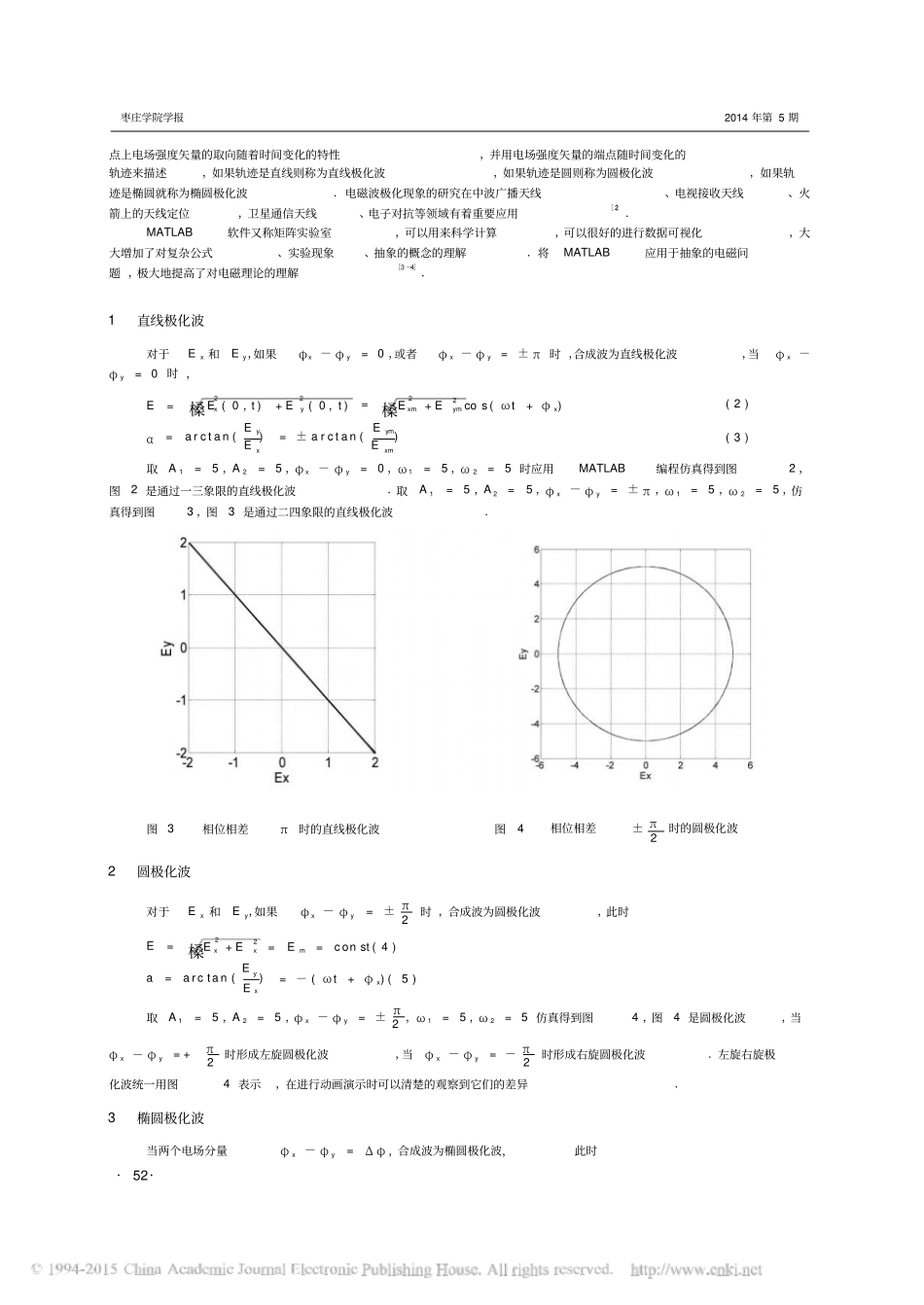
电磁波极化特性的仿真MATLAB闫昕,朱峻锋,赵小新(枣庄学院光电工程学院,山东枣庄277160)[摘要]基于电磁理论的基本知识,应用MATLAB仿真直线极化波、圆极化波和椭圆极化波的电磁波极化特性,研究结论为电磁波极化现象的理解提供新的手段.[关键词]电磁波极化;MATLAB仿真;直线极化波;圆极化波;椭圆极化波①[中图分类号]O442[文献标识码]A[文章编号]1004-7077(2014)05-0051-03引言0库仑定律、安培定律和法拉第电磁感应定律三大电磁学实验定律的提出,标志着人类对宏观电磁现象的认识从定性阶段到定量阶段的飞跃,以三大实验定律为基础,麦克斯韦基于两个假设总结出麦克斯韦方程组描绘电磁波传播、辐射等电磁现象的总规律[1].图1是平面电磁波在无界空间中的传播特性图,从图1中可以看到,平面电磁波沿着→→Z方向传播,电场强度E与磁场强度H处于与电磁波传播的Z方向垂直的无限大平面内.→一般情况下电场强度E有Ex和Ey分量,合成波电场→→E=exEx→+eyEy,其中ExExmcos(ωt+φx),EyEymcos(ωt+φy)(1)==图1平面电磁波在无界空间的传播图2相位相等时的直线极化波→由于Ex和Ey分量的振幅和相位不一定相同,因此在空间任意点上合成波电场强度E的大小和方向都将随着时间变化,这种现象称为电磁波的极化现象.它表征在空间给定[收稿日期]2014-06-10[基金项目]地方高校国家级大学生创新创业训练计划项目(项目编号:201310904024);枣庄学院《电磁场理论》精品课程项目;枣庄学院教学改革项目(项目编号:YJG11007);枣庄学院2014校级大学生研究训练计划项目(项目编号:2014041).[作者简介]闫昕(1977-),男,山东枣庄人,枣庄学院光电工程学院讲师,博士,主要从事计算电磁学、人工晶体和电磁超材料方面的研究.·51·①枣庄学院学报2014年第5期点上电场强度矢量的取向随着时间变化的特性,并用电场强度矢量的端点随时间变化的轨迹来描述,如果轨迹是直线则称为直线极化波,如果轨迹是圆则称为圆极化波,如果轨迹是椭圆就称为椭圆极化波.电磁波极化现象的研究在中波广播天线、电视接收天线、火箭上的天线定位,卫星通信天线、电子对抗等领域有着重要应用[2].MATLAB软件又称矩阵实验室,可以用来科学计算,可以很好的进行数据可视化,大大增加了对复杂公式、实验现象、抽象的概念的理解.将MATLAB应用于抽象的电磁问题,极大地提高了对电磁理论的理解[3-4].直线极化波1对于Ex和Ey,如果φx-φyφy=0时,=0,或者φx-φy=±π时,合成波为直线极化波,当φx-22E=槡E(0,t)+E(0,t)2槡E+E2cos(ωt+φ)(2)=xyxmymxEyEym=arctan()=±arctan()EE(3)αxxm取A1=5,A2=5,φx-φy=0,ω1=5,ω2=5时应用MATLAB编程仿真得到图2,图2是通过一三象限的直线极化波.取A1=5,A2=5,φx-φy=±π,ω1=5,ω2=5,仿真得到图3,图3是通过二四象限的直线极化波.相位相差±π时的圆极化波图3相位相差π时的直线极化波图42圆极化波2π2对于Ex和Ey,如果φx-φy时,合成波为圆极化波,此时=±2槡E+E2=E=const(4)E=xxma=arctan(Ey)=-(ωt+φ)(5)xExπ取A1=5,A2=5,φx-φy=±2,ω1=5,ω2=5仿真得到图4,图4是圆极化波,当π2π2时形成左旋圆极化波,当φx-φy时形成右旋圆极化波.左旋右旋极φx-φy=+=-化波统一用图4表示,在进行动画演示时可以清楚的观察到它们的差异.椭圆极化波3当两个电场分量φx-φy·52·Δφ,合成波为椭圆极化波,此时=闫昕,朱峻锋,赵小新电磁波极化特性的MATLAB仿真E2E2EExyxy2(6)+-E2Ecosφ=sinφE2Exmymxmym2ExmEym(7)tan2θ=cosφE22-Eymxm取A1=5,A2=5,ω1=5,ω2=5,当0<φ<π时仿真得到左旋椭圆极化波,如图5所示.当π<φ<2π时仿真得到右旋椭圆极化波,如图6所示.3π相位相差π时左旋椭圆极化波图5图6相位相差时右旋椭圆极化波444结论从电磁波传播的基本理论方程出发,分析了振幅、相位和合成波夹角变化的理论公式,应用MATLAB语言仿真得到了直线极化波、圆极化波和椭圆极化波的变化图形,对于圆极化波,左旋和右旋不能够通过文中图形判断得到,要根据实际作图的动画判断.研究结论是将MATLAB编程应用到电磁波极化的仿真...