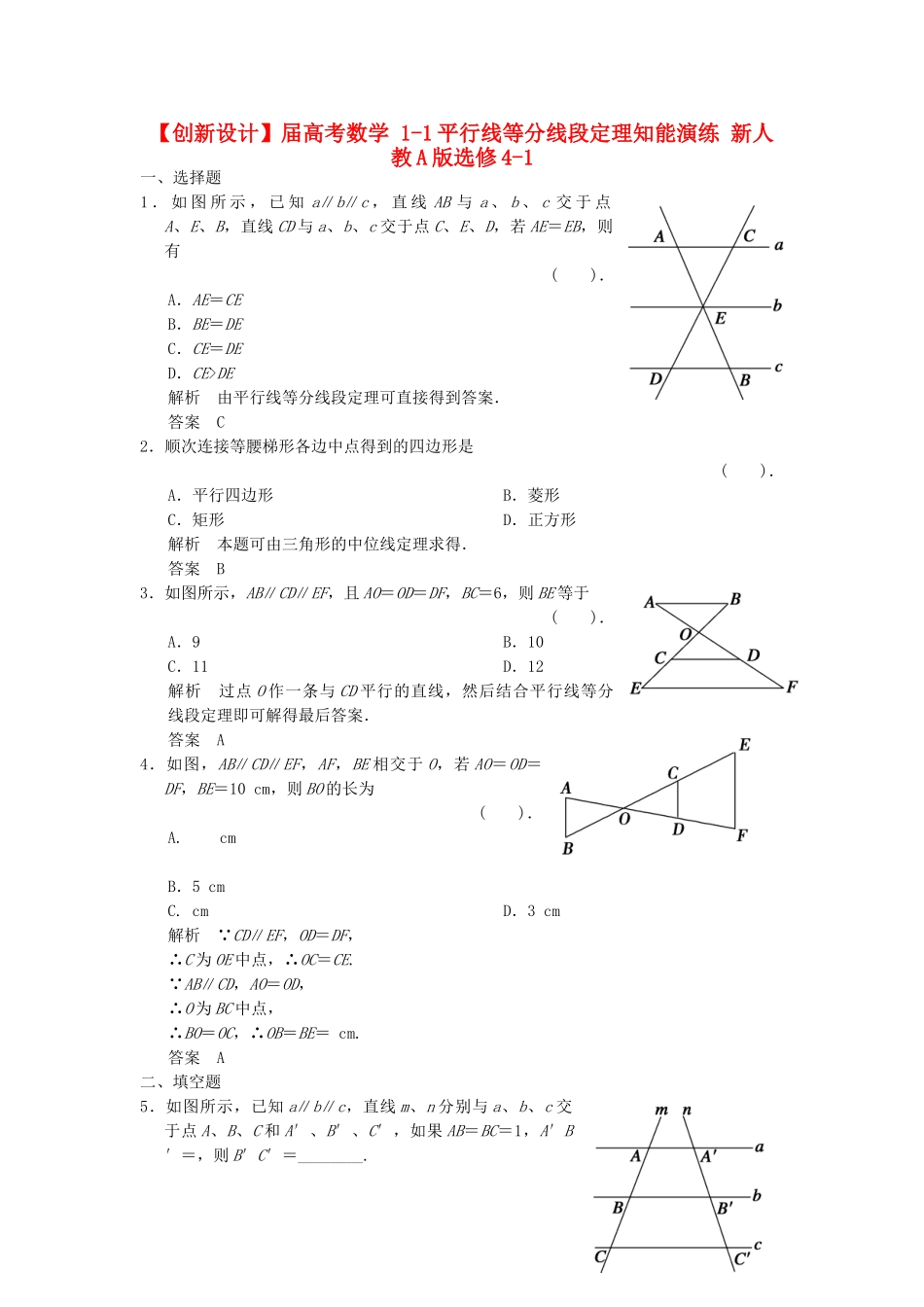
【创新设计】届高考数学1-1平行线等分线段定理知能演练新人教A版选修4-1一、选择题1.如图所示,已知a∥b∥c,直线AB与a、b、c交于点A、E、B,直线CD与a、b、c交于点C、E、D,若AE=EB,则有().A.AE=CEB.BE=DEC.CE=DED.CE>DE解析由平行线等分线段定理可直接得到答案.答案C2.顺次连接等腰梯形各边中点得到的四边形是().A.平行四边形B.菱形C.矩形D.正方形解析本题可由三角形的中位线定理求得.答案B3.如图所示,AB∥CD∥EF,且AO=OD=DF,BC=6,则BE等于().A.9B.10C.11D.12解析过点O作一条与CD平行的直线,然后结合平行线等分线段定理即可解得最后答案.答案A4.如图,AB∥CD∥EF,AF,BE相交于O,若AO=OD=DF,BE=10cm,则BO的长为().A.cmB.5cmC.cmD.3cm解析∵CD∥EF,OD=DF,∴C为OE中点,∴OC=CE.∵AB∥CD,AO=OD,∴O为BC中点,∴BO=OC,∴OB=BE=cm.答案A二、填空题5.如图所示,已知a∥b∥c,直线m、n分别与a、b、c交于点A、B、C和A′、B′、C′,如果AB=BC=1,A′B′=,则B′C′=________.解析由平行线等分线段定理可直接得到答案.答案6.在梯形ABCD中,M、N分别是腰AB和腰CD的中点,且AD=2,BC=4,则MN=________.解析由梯形的中位线定理直接可得.答案37.梯形的中位线长10cm,一条对角线将中位线分成的两部分之差是3cm,则该梯形中的较大的底是________cm.解析设梯形较大,较小的底分别为a,b,则有可得:a=13.答案138.如图,在△ABC中,E是AB的中点,EF∥BD,EG∥AC交BD于G,CD=AD,若EG=5cm,则AC=________cm;若BD=20cm,则EF=________cm.解析∵E为AB的中点,EF∥BD,∴F为AD的中点.∵E为AB的中点,EG∥AC,∴G为BD的中点,若EG=5cm,则AD=10cm.又CD=AD=5cm,∴AC=15cm.若BD=20cm,则EF=BD=10cm.答案1510三、解答题9.如图所示,在梯形ABCD中,AD∥BC,DC⊥BC,∠B=60°,BC=AB,E为AB的中点.求证:△ECD为等边三角形.证明过E作EF∥BC交DC于F,连接AC,如图所示.∵AD∥BC,E为AB中点,∴F是DC中点.①又∵DC⊥BC,EF∥BC,∴EF⊥DC.②∴由①②知,EF是DC的垂直平分线,∴△ECD为等腰三角形.③∵BC=AB,∠B=60°,∴△ABC是等边三角形.又∵E是AB中点,∴CE是∠ACB的平分线,∴∠BCE=30°.∴∠ECD=60°.④由③④知,△ECD为等边三角形.10.如图,在▱ABCD中,E和F分别是边BC和AD的中点,BF和DE分别交AC于P、Q两点.求证:AP=PQ=QC.证明∵四边形ABCD是平行四边形,E、F分别是BC、AD边上的中点,∴DF綉BE,∴四边形BEDF是平行四边形.∵在△ADQ中,F是AD的中点,FP∥DQ.∴P是AQ的中点,∴AP=PQ.∵在△CPB中,E是BC的中点,EQ∥BP,∴Q是CP的中点,∴CQ=PQ,∴AP=PQ=QC.11.(拓展深化)如图,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,DC的延长线交BE于F,求证:EF=BF.证明如图所示,连接AE交DC于O.∵四边形ACED是平行四边形.∴O是AE的中点.∵在梯形ABCD中,DC∥AB,在△EAB中,OF∥AB,又∵O是AE的中点,∴F是EB的中点,∴EF=BF.