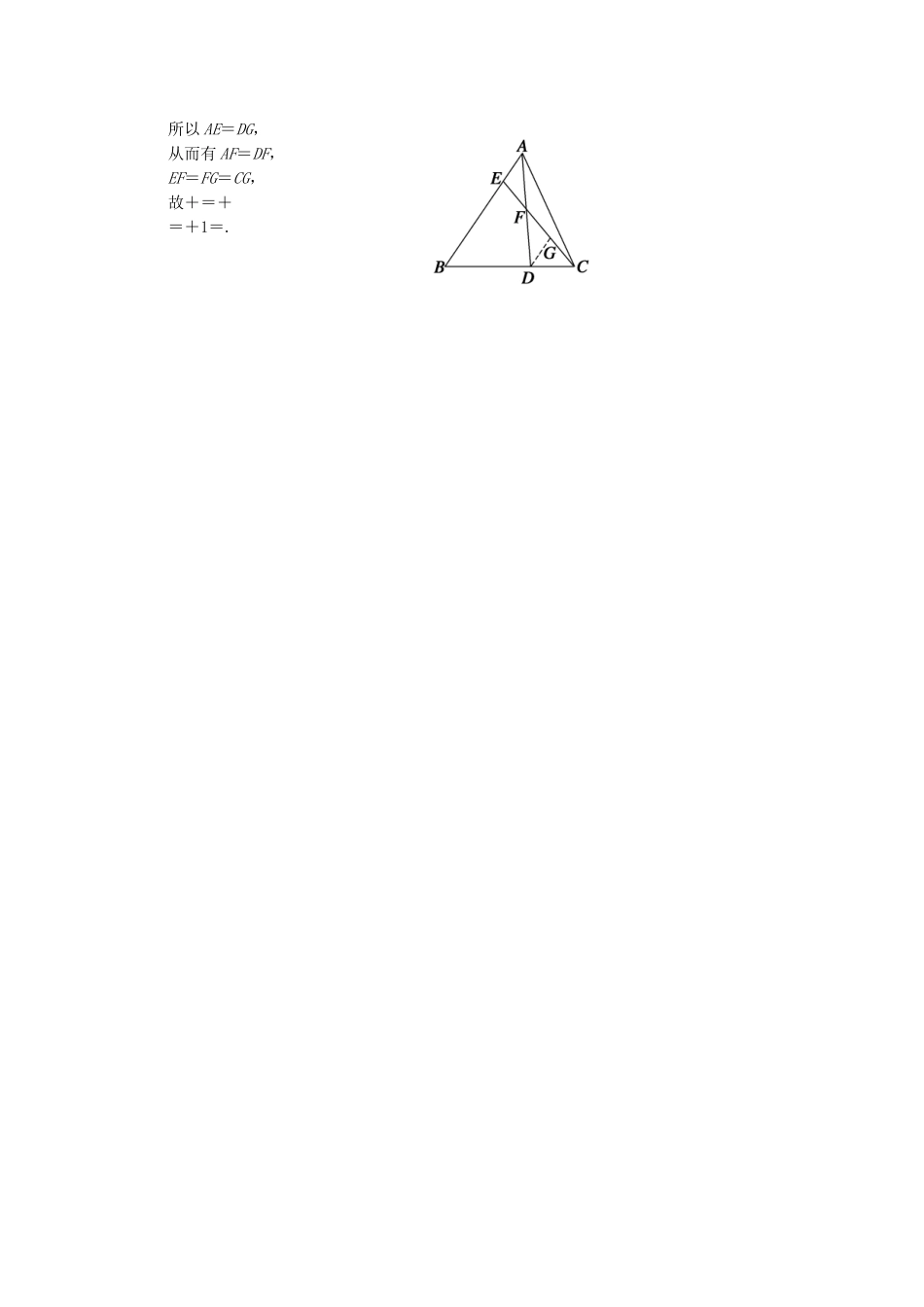
【创新设计】届高考数学1-2平行线分线段成比例定理知能演练新人教A版选修4-1一、选择题1.若=,则下列各式一定成立的是().A.=B.=C.=D.=解析=⇒ad=bc.=⇒ac=bd,∴A不正确.=⇒ad=bc,∴B正确.同理知C、D均不正确.答案B2.如图,已知AB∥CD∥EF,那么下列结论正确的是().A.=B.=C.=D.=答案A3.如图所示,在△ACE中,B、D分别在AC、AE上,下列推理不正确的是().A.BD∥CE⇒=B.BD∥CE⇒=C.BD∥CE⇒=D.BD∥CE⇒=解析由平行线分线段成比例定理的推论不难得出A、B、C都是正确的,D是错误的,故选D.答案D4.如图所示,AD是△ABC的中线,E是CA边的三等分点,BE交AD于点F,则AF∶FD为().A.2∶1B.3∶1C.4∶1D.5∶1解析要求AF∶FD的比,需要添加平行线寻找与之相等的比.注意到D是BC的中点,可过D作DG∥AC交BE于G,则DG=EC,又AE=2EC,故AF∶FD=AE∶DG=2EC∶EC=4∶1.答案C二、填空题5.如图所示,在△ABC中,MN∥DE∥BC,若AE∶EC=7∶3,则DB∶AB的值为________.解析由AE∶EC=7∶3,有EC∶AC=3∶10.根据MN∥DE∥BC,可得DB∶AB=EC∶AC,即得结论.答案3∶106.如图所示,已知a∥b,=,=3,则AE∶EC=________.解析∵a∥b,∴=,=.∵=3,∴BC=3CD,∴BD=4CD.又∵=,∴==,∴=,∴=.∴==.答案7.如图所示,l1∥l2∥l3,若CH=4.5cm,AG=3cm,BG=5cm,EF=12.9cm,则DH=________,EK=________.解析由l1∥l2∥l3,可得=,所以DH===7.5(cm),同理可得EK的长度.答案7.5cm34.4cm8.如图所示,已知DE∥BC,BF∶EF=3∶2,则AC∶AE=________,AD∶DB=________.解析∵DE∥BC,∴==.∵BF∶EF=3∶2,∴==.∴AC∶AE=3∶2.同理DE∥BC,得AB∶AD=3∶2,即=.∴=.即==2,即=2.∴AD∶BD=2∶1.答案3∶22∶1三、解答题9.如图所示,已知平面α∥平面β,点P是平面α、β外一点,且直线PAB、PCD分别与α、β相交于A、B、C、D.(1)求证:AC∥BD;(2)如果PA=4cm,AB=5cm,PC=3cm,求PD的长.(1)证明∵α∥β,平面PBD∩α=AC,平面PBD∩β=BD,∴AC∥BD.(2)解∵AC∥BD,∴=,∴=,∴CD=,∴PD=3+=.10.已知AD是△ABC的内角平分线,求证:=.证明过C作CE∥AD交BA的延长线于E,如图所示,则∠AEC=∠BAD,∠DAC=∠ACE.又∠BAD=∠DAC,∴∠AEC=∠ACE,∴AC=AE,又由AD∥CE知=,∴=.11.(拓展深化)如图所示,已知△ABC中,AE∶EB=1∶3,BD∶DC=2∶1,AD与CE相交于F,求+的值.解过点D作DG∥AB交EC于G,则===,而=,即=,所以AE=DG,从而有AF=DF,EF=FG=CG,故+=+=+1=.