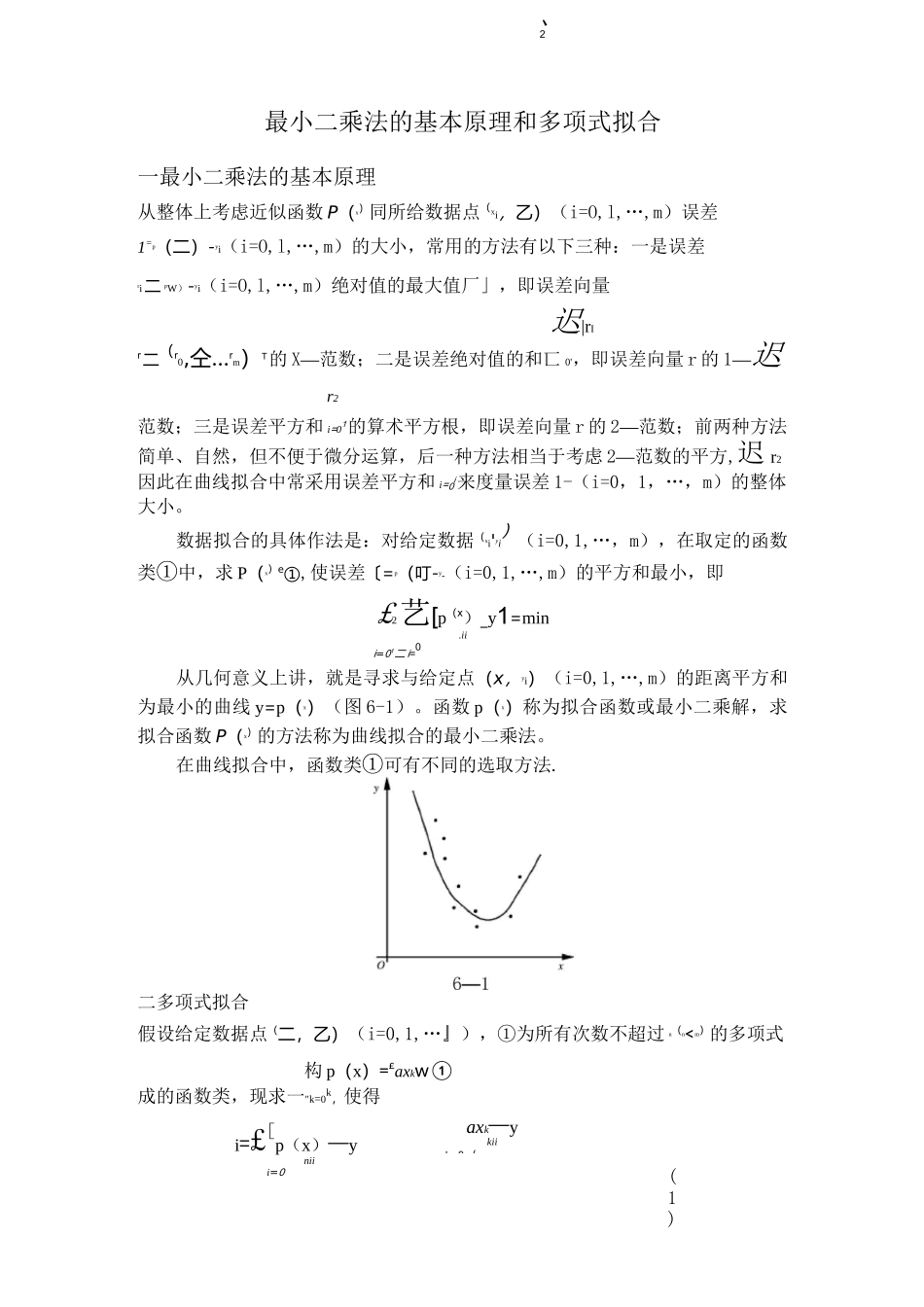
、2(1)=minaxk—ykiik=0丿最小二乘法的基本原理和多项式拟合一最小二乘法的基本原理从整体上考虑近似函数P(x)同所给数据点(Xi,乙)(i=O,l,…,m)误差1=p(二)-yi(i=O,l,…,m)的大小,常用的方法有以下三种:一是误差ri二pW)-yi(i=O,l,…,m)绝对值的最大值厂」,即误差向量迟|rIr二(r0,仝…rm)T的X—范数;二是误差绝对值的和匸0',即误差向量r的1—迟r2范数;三是误差平方和i=01的算术平方根,即误差向量r的2—范数;前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑2—范数的平方,迟r2因此在曲线拟合中常采用误差平方和i=0i来度量误差1-(i=0,1,…,m)的整体大小。数据拟合的具体作法是:对给定数据(xi'yi)(i=0,1,…,m),在取定的函数类①中,求P(x)e①,使误差〔=p(叮-y-(i=0,1,…,m)的平方和最小,即£2艺[p(x)_y1=min.iii=01二i=0从几何意义上讲,就是寻求与给定点(x,yi)(i=0,1,…,m)的距离平方和为最小的曲线y=p(x)(图6-1)。函数p(x)称为拟合函数或最小二乘解,求拟合函数P(x)的方法称为曲线拟合的最小二乘法。在曲线拟合中,函数类①可有不同的选取方法.二多项式拟合假设给定数据点(二,乙)(i=0,1,…』),①为所有次数不超过n(n