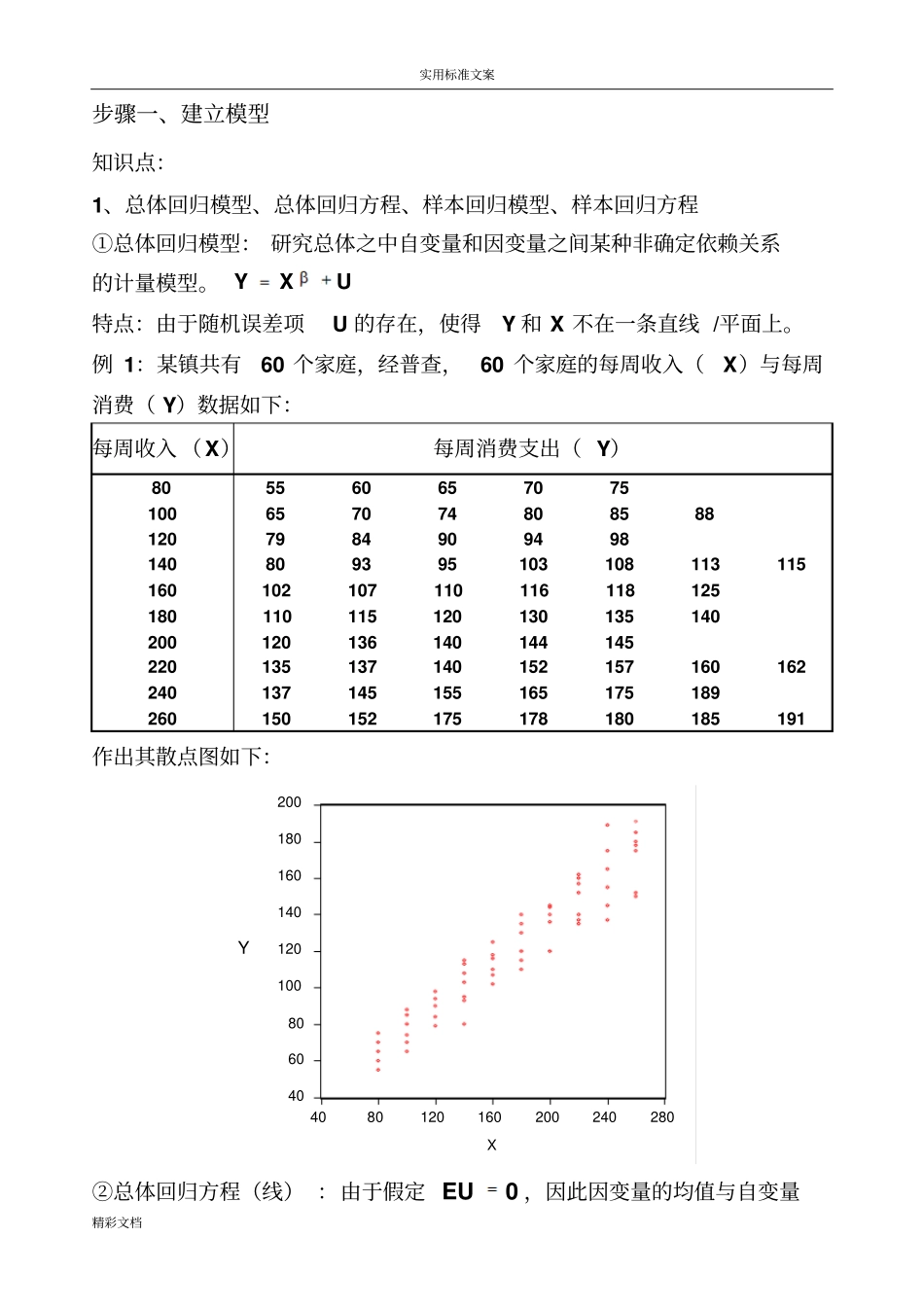
实用标准文案精彩文档步骤一、建立模型知识点:1、总体回归模型、总体回归方程、样本回归模型、样本回归方程①总体回归模型:研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。YXU特点:由于随机误差项U的存在,使得Y和X不在一条直线/平面上。例1:某镇共有60个家庭,经普查,60个家庭的每周收入(X)与每周消费(Y)数据如下:每周收入(X)每周消费支出(Y)8055606570751006570748085881207984909498140809395103108113115160102107110116118125180110115120130135140200120136140144145220135137140152157160162240137145155165175189260150152175178180185191作出其散点图如下:4060801001201401601802004080120160200240280XY②总体回归方程(线):由于假定0EU,因此因变量的均值与自变量实用标准文案精彩文档总处于一条直线上,这条直线|EYXX就称为总体回归线(方程)。总体回归方程的求法:以例1的数据为例1)对第一个Xi,求出E(Y|Xi)。每周收入(X)每周消费支出(Y)E(Y|Xi)8055606570756510065707480858877120798490949889140809395103108113115101160102107110116118125113180110115120130135140125200120136140144145137220135137140152157160162149240137145155165175189161260150152175178180185191173由于01|iiiEYXX,因此任意带入两个Xi和其对应的E(Y|Xi)值,即可求出01和,并进而得到总体回归方程。如将222777100,|77200,|137XEYXXEYX和代入01|iiiEYXX可得:01001177100171372000.6以上求出01和反映了E(Y|Xi)和Xi之间的真实关系,即所求的总体回归方程为:|170.6iiiEYXX,其图形为:4060801001201401601802004080120160200240280XYYvs.X实用标准文案精彩文档③样本回归模型:总体通常难以得到,因此只能通过抽样得到样本数据。如在例1中,通过抽样考察,我们得到了20个家庭的样本数据:每周收入(X)每周消费支出(Y)8055100657012079841408093160102107110180110200120136220135137240137145260150152175那么描述样本数据中因变量Y和自变量X之间非确定依赖关系的模型?YXe就称为样本回归模型。④样本回归方程(线):通过样本数据估计出?,得到样本观测值的拟合值与解释变量之间的关系方程??YX称为样本回归方程。如下图所示:4060801001201401601804080120160200240280XYYvs.X⑤四者之间的关系:ⅰ:总体回归模型建立在总体数据之上,它描述的是因变量Y和自变量X实用标准文案精彩文档之间的真实的非确定型依赖关系;样本回归模型建立在抽样数据基础之上,它描述的是因变量Y和自变量X之间的近似于真实的非确定型依赖关系。这种近似表现在两个方面:一是结构参数?是其真实值的一种近似估计;二是残差e是随机误差项U的一个近似估计;ⅱ:总体回归方程是根据总体数据得到的,它描述的是因变量的条件均值E(Y|X)与自变量X之间的线性关系;样本回归方程是根据抽样数据得到的,它描述的是因变量Y样本预测值的拟合值?Y与自变量X之间的线性关系。ⅲ:回归分析的目的是试图通过样本数据得到真实结构参数的估计值,并要求估计结果?足够接近真实值。由于抽样数据有多种可能,每一次抽样所得到的估计值?都不会相同,即的估计量?是一个随机变量。因此必须选择合适的参数估计方法,使其具有良好的统计性质。2、随机误差项U存在的原因:①非重要解释变量的省略②人的随机行为③数学模型形式欠妥④归并误差(如一国GDP的计算)⑤测量误差等3、多元回归模型的基本假定①随机误差项的期望值为零()0iEU②随机误差项具有同方差性2()1,2,,iVaruin③随机误差项彼此之间不相关(,)0;,1,2,,ijCovuuijijn④解释就变量X1,X2,···,Xk为确定型变量,与随机误差项彼此不相关。实用标准文案精彩文档(,)01,2,,1,2,,ijjCovXuikjn⑤解释就变量X1,X2,···,Xk之间不存在精确的(完全的)线性关系,即解释变量的样本观测值矩阵X为满秩矩阵:rank(X)=k+1