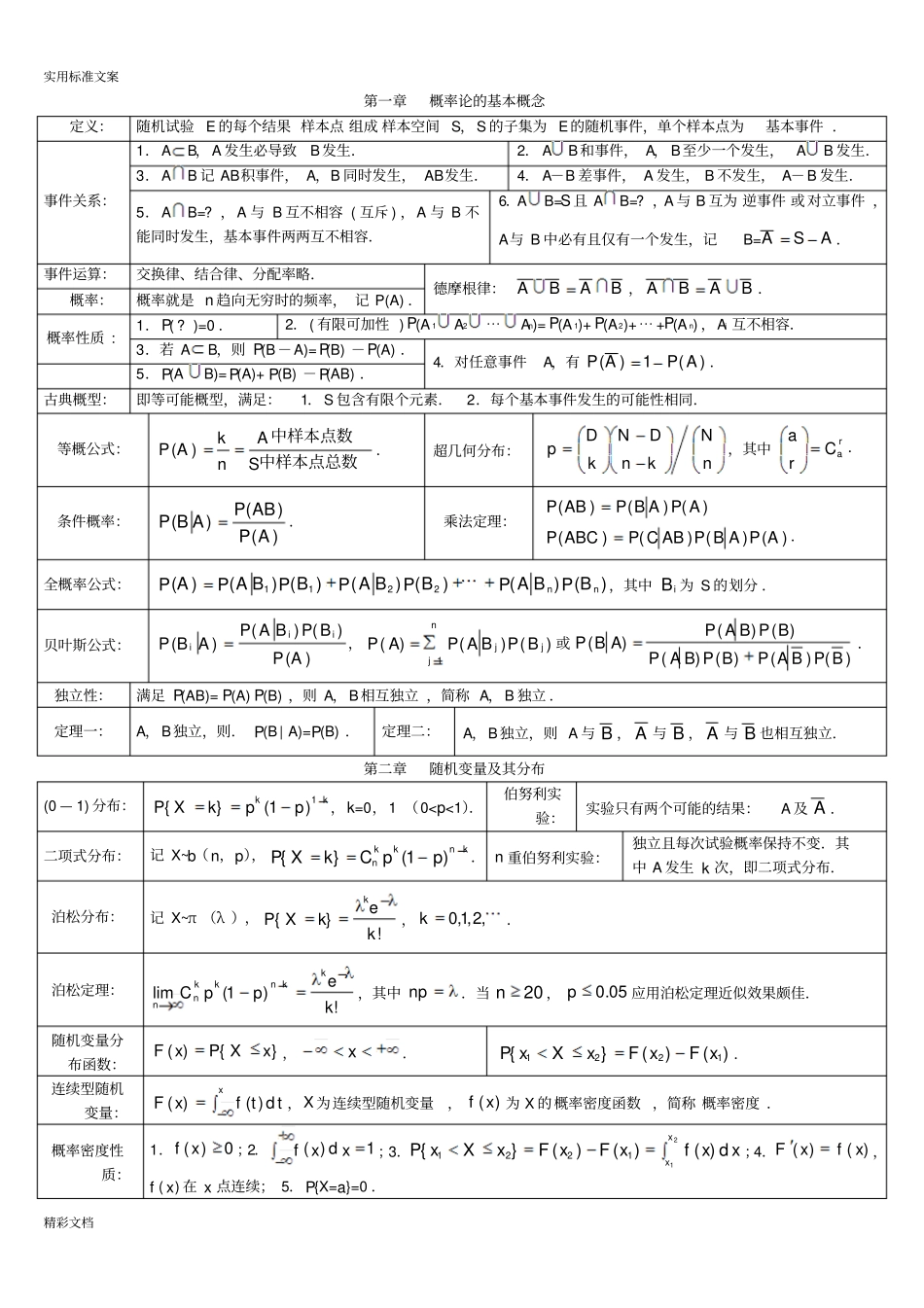
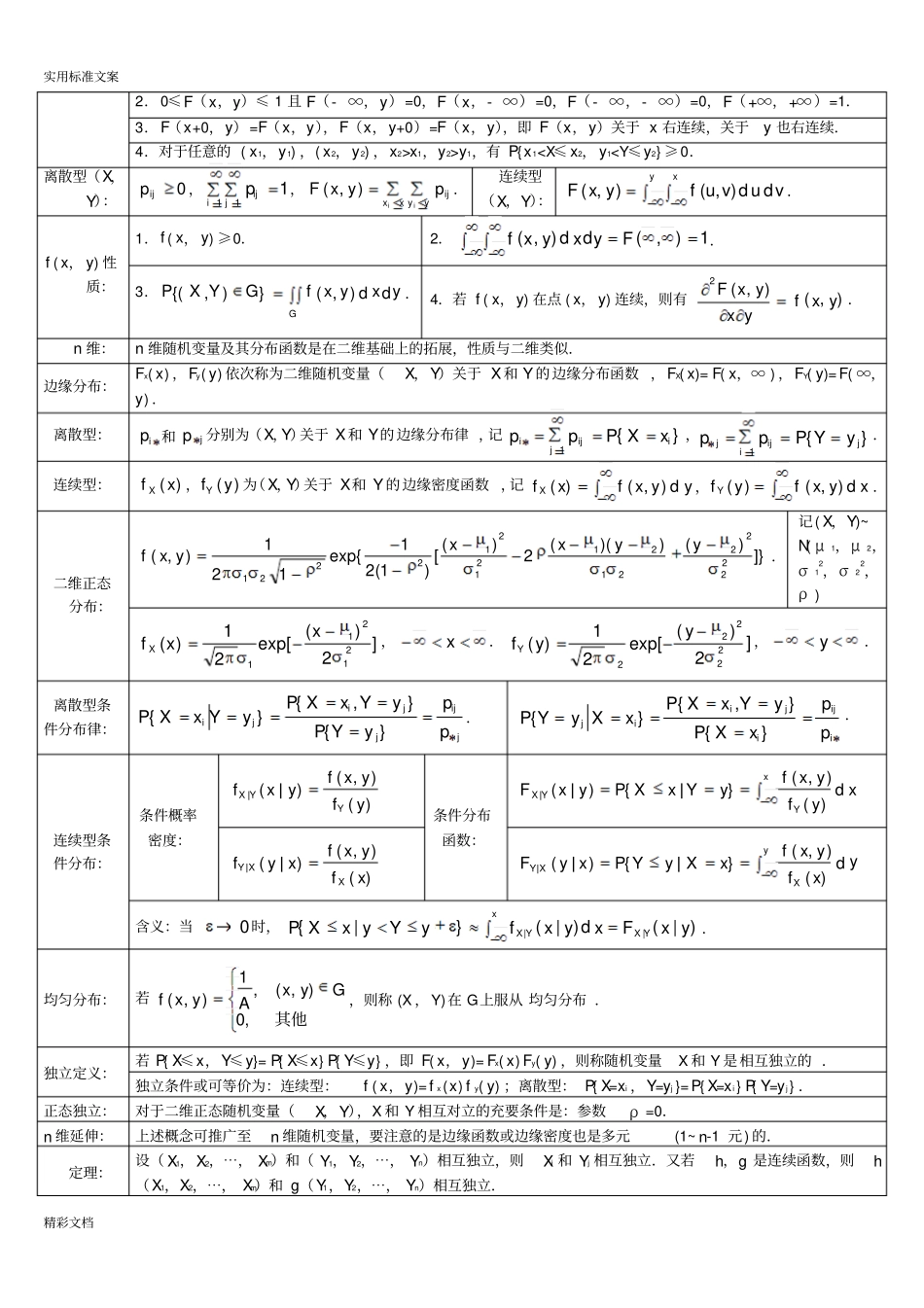
实用标准文案精彩文档第一章概率论的基本概念定义:随机试验E的每个结果样本点组成样本空间S,S的子集为E的随机事件,单个样本点为基本事件.事件关系:1.AB,A发生必导致B发生.2.AB和事件,A,B至少一个发生,AB发生.3.AB记AB积事件,A,B同时发生,AB发生.4.A-B差事件,A发生,B不发生,A-B发生.5.AB=?,A与B互不相容(互斥),A与B不能同时发生,基本事件两两互不相容.6.AB=S且AB=?,A与B互为逆事件或对立事件,A与B中必有且仅有一个发生,记B=ASA.事件运算:交换律、结合律、分配率略.德摩根律:BABA,BABA.概率:概率就是n趋向无穷时的频率,记P(A).概率性质:1.P(?)=0.2.(有限可加性)P(A1A2⋯An)=P(A1)+P(A2)+⋯+P(An),Ai互不相容.3.若AB,则P(B-A)=P(B)-P(A).4.对任意事件A,有)A(1)A(PP.5.P(AB)=P(A)+P(B)-P(AB).古典概型:即等可能概型,满足:1.S包含有限个元素.2.每个基本事件发生的可能性相同.等概公式:中样本点总数中样本点数SA)A(nkP.超几何分布:nNknDNkDp,其中raCra.条件概率:)A()AB()AB(PPP.乘法定理:)A()AB()ABC()ABC()A()AB()AB(PPPPPPP.全概率公式:)B()BA()B()BA()B()BA()A(2211nnPPPPPPP,其中iB为S的划分.贝叶斯公式:)A()B()BA()AB(PPPPiii,njjjBPBAPAP1)()()(或)()()()()()()(BPBAPBPBAPBPBAPABP.独立性:满足P(AB)=P(A)P(B),则A,B相互独立,简称A,B独立.定理一:A,B独立,则.P(B|A)=P(B).定理二:A,B独立,则A与B,A与B,A与B也相互独立.第二章随机变量及其分布(0—1)分布:kkppkXP1)1(}{,k=0,1(0
zα}=α,0<α<1,则称点zα为标准正态分布的上α分位点.常用上ɑ分位点:0.0010.0050.010.0250.050.103.0902.5762.3261.9601.6451.282Y服从自由度为1的χ2分布:设X密度函数fX(x),x,若Y=X2,则000)]()([21)(yyyfyfyyfXXY,,若设X~N(0,1),则有00021)(221yyeyyfyY,,定理:设X密度函数fX(x),设g(x)处处可导且恒有g′(x)>0(或g′(x)<0),则Y=g(X)是连续型随机变量,且有其他,,0)()]([)(yyhyhfyfXYh(y)是g(x)的反函数;①若x,则α=min{g(-∞),g(+∞)},β=max{g(-∞),g(+∞)};②若fX(x)在[a,b]外等于零,g(x)在[a,b]上单调,则α=min{g(a),g(b)},β=max{g(a),g(b)}.应用:Y=aX+b~N(aμ+b,(|a|σ)2).第三章多维随机变量及其分布二维随机变量的分布函数:分布函数(联合分布函数):)}(){(),(yYxXPyxF,记作:},{yYxXP.),(),(),(),(},{112112222121yxFyxFyxFyxFyYyxXxP.F(x,y)性质:1.F(x,y)是x和y的不减函数,即x2>x1时,F(x2,y)≥F(x...