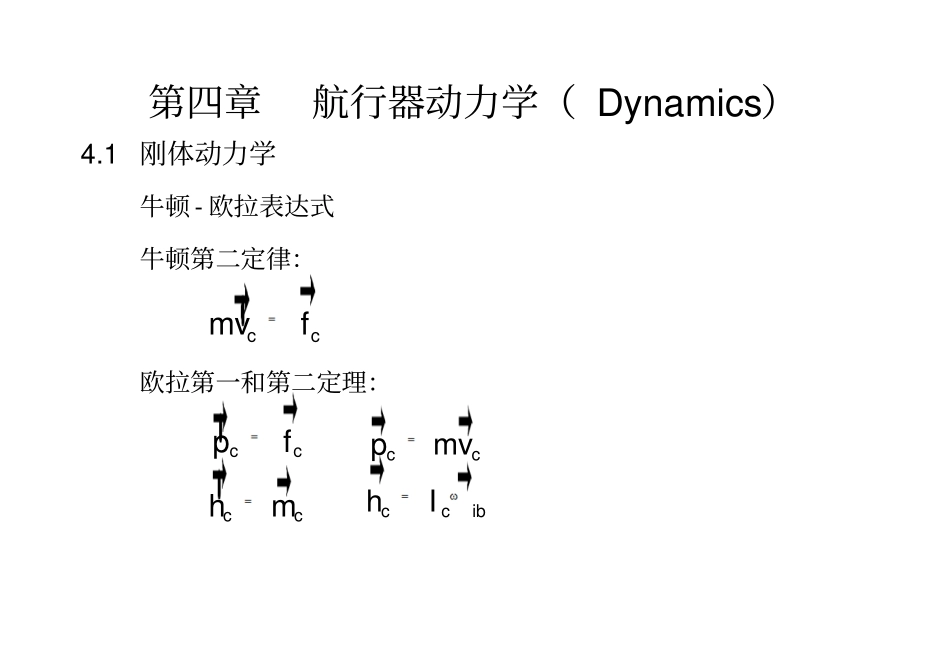
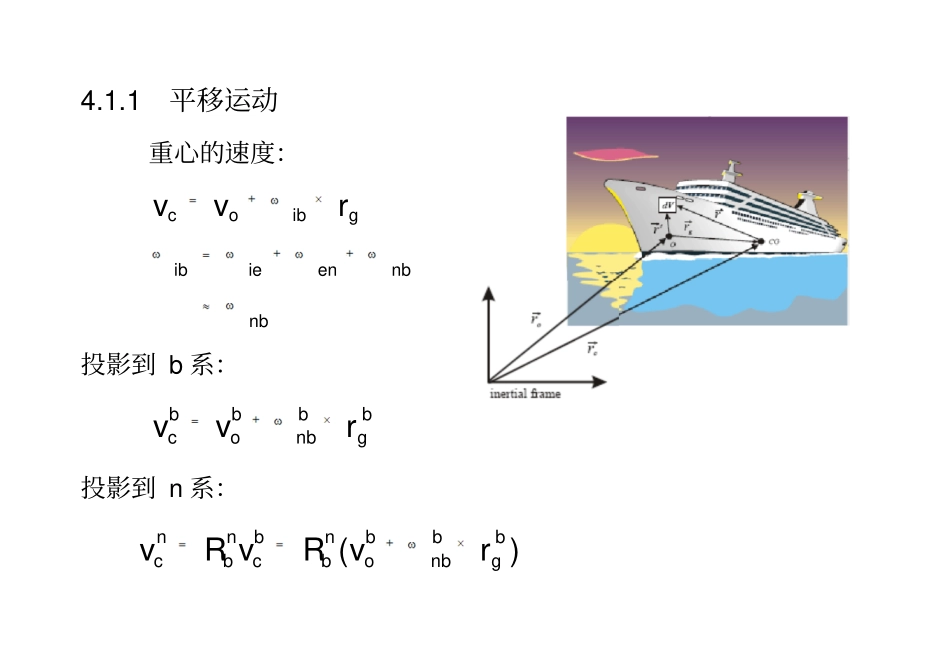
第四章航行器动力学(Dynamics)4.1刚体动力学牛顿-欧拉表达式牛顿第二定律:ccmvf欧拉第一和第二定理:ccccpfhmccccibpmvhI4.1刚体动力学假设:(1)航行器是个刚体;(2)NED坐标系是惯性坐标系;第一个假设可以不用考虑航行器各质量元素之间的相互作用力;第二个假设可以不用考虑由于地球自转而产生的力,这是因为地球自转的角速度为:57.292110(/)ierads地球自转产生的力相对于水动力来说可以忽略。4.1.1平移运动重心的速度:coibgvvribieennbnb投影到b系:bbbbconbgvvr投影到n系:()nnbnbbbcbcbonbgvRvRvr4.1.1平移运动对上式求导:2()()()()()[()()()]nnbbbbbnbbbcbonbgnbgbonbgnbbbnbbbbbonbgbnbonbgnbbbbbbbbonbgnbonbgvRvrrRvrRvrRSvrRvSrSvSr根据欧拉第一定理:iiccmvfNED近似为惯性系,nnnbccbcmvfRf2[()()()]bbbbbbbbbonbgnbonbgcomvSrSvSrff4.1.1平移运动[()]bbbbbbbbbonbgnbonbnbgomvrvrf如果b系的原点选在重心,则000,,Tbbbbbgococrffvv则:[()]bbbbcnbccmvSvf4.1.2旋转运动欧拉第二定理:,ccccibhmhI根据前面的假设,可以得到()()()()bbbbbbbbbonbnbonbgognbooISImSrvmSrSvm式中::,0xxyxzToyxyyzoozxzyzIIIIIIIIIIII4.1.2旋转运动222222();();();xmxymmyxVVVymxzmmzxVVVzmyzmmzyVVVIyzdVIxydVyxdVIIxzdVIxzdVzxdVIIxydVIyzdVzydVI如果b系的原点选在重心,即000Tbgr则()bbbbonbnbonbcISIm4.1.2旋转运动平行轴定理:相对于任意原点o的惯性矩阵可以表示为:233()()bTTocgcIImSrImrrrrI4.1.3刚体动力学方程2[()()()]bbbbbbbbbonbgnbonbgcomvSrSvSrff()()()()bbbbbbbbbonbnbonbgognbooISImSrvmSrSvm4.1.3刚体动力学方程矩阵向量形式:(),RBRBRBMCuvwpqrvvvv特性:660,0TRBRBRBMMM33()()000000000000bgRBbgoggggggggxxyxzggyxyyzggzxzyzmImSrMmSrImmzmymmzmxmmymxmzmyIIImzmxIIImymxIII4.1.3刚体动力学方程定理:令M为66的系统惯性矩阵:111221220TMMMMMM其中:2112TMM。则科里奥利—向心矩阵为反对称矩阵,并可表示为:331111221111222112220()()()()SMvMvCvSMvMvSMvMv式中,12,TTvuvwvpqr。4.1.3刚体动力学方程特性(刚体科里奥利—向心矩阵)刚体科里奥利—向心矩阵()RBCv总可以表示为反对称矩阵,即6()(),TRBRBCvCvv将RBM代入得:331212120()(())()()(())(())()bgRBbbggomSvmSSvrCvmSvmSSvrmSSvrSIv4.1.3刚体动力学方程刚体六自由度运动方程的简化:(1)原点o与重心一致:000Tbgr3333330,0xxyxzcoyxyyzRBczxzyzIIImIIIIIIMIIII进一步简化:coxyzIIdiagIII4.1.3刚体动力学方程刚体六自由度运动方程的简化:(2)旋转载体系的坐标轴,使得oI为对角矩阵。求oI的特征值(1,2,3)ii:3233210det()0oIIaaa求模态矩阵123Hhhh:33()0;(1,2,3)ioiIIhi将坐标系(,,)bbbxyz旋转到新坐标系(,,)bbbxyz,它的单位向量为4.1.3刚体动力学方程刚体六自由度运动方程的简化:(2)旋转载体系的坐标轴,使得oI为对角矩阵。;;xxyyzzeHeeHeeHe则新的惯性矩阵123oIdiag();();();();();();xzyyxzzyxmuvrwqxIpIIqrKmvwpuryIqIIrpMmwuqvpzIrIIpqN4.1.3刚体动力学方程刚体六自由度运动方程的简化:(3)平移原点o使得oI为对角阵。oxyzIdiagIII由平行轴定理:2()cgcgcgxxyxzbcgcgcgcogyxyyzcgcgcgzxzyzIIIIImSrIIIIII对角元素必须满足:4.1.3刚体动力学方程刚体六自由度运动方程的简化:(3)平移原点o使得oI为对角阵。222222()()()cgxxggcgyyggcgzzggIImyzIImxzIImxy选择,,gggxyz,使得222cgcgcgyzgxyxzcgcgcgxzgxyyzcgcgcgxygxzyzmIxIImIyIImIzII4.1.3刚体动力学方程刚体六自由度运动方程的简化:(3)平移原点o使得oI为对角阵。此时刚体动力学方程为:222222()()()()()()()()()()()()()gggggggggxzyggyxzgmuvrwqxqrypqrzprqXmvwpuryrpzqrpxqprYmwuqvpzpqxrpqyrqpZIpIIqrmywuqvpzvwpurKIqIIrpmz()()()()()gzyxgguvrwqxwuqvpMIrIIpqmxvwpuryuvrwqN4.2流体动力和力矩(1)由于流体辐射引起的力:0addedmasspotentialdampingrestoringforces()()()RAAPMvCvvDvvggvortexsheddingdampingskinfrictionwavedriftdamping()()()DSwMDvvDvvDvv令:():()()()()PSWMDvDvDvDvDv0()()()HRDAAMvCvvDvvgg(2)由...